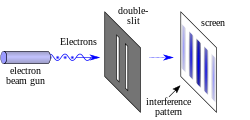
Experimento de fenda dupla

Fotões ou partículas de matéria (como um elétron) produzem um padrão de onda quando duas fendas são usadas

Luz de um laser verde passando por duas fendas 0.4mm de largura e 0.1mm de distância

Na física moderna, o experimento da fenda dupla é uma demonstração de que a luz e a matéria podem exibir características de ondas e partículas classicamente definidas; além disso, mostra a natureza fundamentalmente probabilística dos fenômenos da mecânica quântica. Esse tipo de experimento foi realizado pela primeira vez por Thomas Young em 1801, como demonstração do comportamento ondulatório da luz visível. Naquela época, pensava-se que a luz consistia em ou ondas ou partículas. Com o início da física moderna, cerca de cem anos depois, percebeu-se que a luz poderia de fato apresentar comportamento característico de ambos ondas e partículas. Em 1927, Davisson e Germer demonstraram que os elétrons apresentam o mesmo comportamento, que mais tarde foi estendido a átomos e moléculas. O experimento de Thomas Young com a luz fazia parte da física clássica muito antes do desenvolvimento da mecânica quântica e do conceito de dualidade onda-partícula. Ele acreditava que isso demonstrava que a teoria ondulatória da luz estava correta, e seu experimento às vezes é chamado de experimento de Young ou fendas de Young.

O experimento pertence a uma classe geral de "caminho duplo" experimentos, nos quais uma onda é dividida em duas ondas separadas (a onda é normalmente feita de muitos fótons e melhor chamada de frente de onda, não confundir com as propriedades de onda do fóton individual) que posteriormente se combinam em uma única onda. Mudanças nos comprimentos de caminho de ambas as ondas resultam em uma mudança de fase, criando um padrão de interferência. Outra versão é o interferômetro Mach-Zehnder, que divide o feixe com um divisor de feixe.

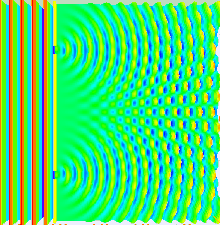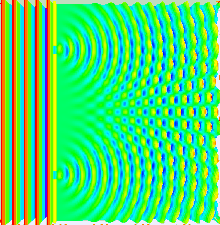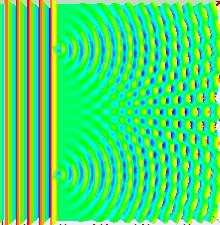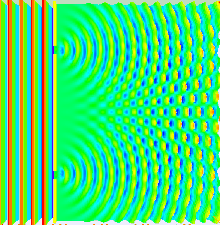
Na versão básica deste experimento, uma fonte de luz coerente, como um feixe de laser, ilumina uma placa perfurada por duas fendas paralelas, e a luz que passa pelas fendas é observada em uma tela atrás da placa. A natureza ondulatória da luz faz com que as ondas de luz que passam pelas duas fendas interfiram, produzindo faixas claras e escuras na tela – um resultado que não seria esperado se a luz consistisse em partículas clássicas. No entanto, a luz é sempre absorvida na tela em pontos discretos, como partículas individuais (não ondas); o padrão de interferência aparece por meio da densidade variável dessas partículas atingidas na tela. Além disso, versões do experimento que incluem detectores nas fendas descobrem que cada fóton detectado passa por uma fenda (como faria uma partícula clássica), e não por ambas as fendas (como faria uma onda). No entanto, tais experimentos demonstram que as partículas não formam o padrão de interferência se for detectado por qual fenda elas passam. Esses resultados demonstram o princípio da dualidade onda-partícula.

Outras entidades em escala atômica, como elétrons, exibem o mesmo comportamento quando disparadas em direção a uma fenda dupla. Além disso, observa-se que a detecção de impactos discretos individuais é inerentemente probabilística, o que é inexplicável usando a mecânica clássica.

O experimento pode ser feito com entidades muito maiores que elétrons e fótons, embora se torne mais difícil à medida que o tamanho aumenta. As maiores entidades para as quais o experimento da dupla fenda foi realizado eram moléculas com 2.000 átomos cada uma (cuja massa total era de 25.000 unidades de massa atômica).

O experimento da dupla fenda (e suas variações) tornou-se um clássico por sua clareza em expressar os quebra-cabeças centrais da mecânica quântica. Por demonstrar a limitação fundamental da capacidade do observador de prever resultados experimentais, Richard Feynman o chamou de "um fenômeno que é impossível [...] de explicar de qualquer maneira clássica, e que tem em si o coração da mecânica quântica.. Na realidade, ele contém o único mistério [da mecânica quântica]."

Visão geral

O mesmo conjunto de fenda dupla (0,7 mm entre fendas); na imagem superior, uma fenda é fechada. Na imagem de fenda única, um padrão de difração (os pontos fracos em ambos os lados da banda principal) forma devido à largura nonzero da fenda. Este padrão de difração também é visto na imagem de dupla fenda, mas com muitas franjas de interferência menores.

Se a luz consistisse estritamente em partículas comuns ou clássicas, e essas partículas fossem disparadas em linha reta através de uma fenda e pudessem atingir uma tela do outro lado, esperaríamos ver um padrão correspondente ao tamanho e forma de a fenda. No entanto, quando esse "experimento de fenda única" é realmente executado, o padrão na tela é um padrão de difração no qual a luz é espalhada. Quanto menor a fenda, maior o ângulo de propagação. A parte superior da imagem mostra a parte central do padrão formado quando um laser vermelho ilumina uma fenda e, se olharmos com atenção, duas faixas laterais fracas. Mais bandas podem ser vistas com um aparelho mais altamente refinado. A difração explica o padrão como sendo o resultado da interferência das ondas de luz da fenda.

Se alguém iluminar duas fendas paralelas, a luz das duas fendas novamente interfere. Aqui a interferência é um padrão mais pronunciado com uma série de faixas claras e escuras alternadas. A largura das bandas é uma propriedade da frequência da luz que ilumina. (Veja a fotografia inferior à direita.) Quando Thomas Young (1773–1829) demonstrou esse fenômeno pela primeira vez, indicou que a luz consiste em ondas, pois a distribuição do brilho pode ser explicada pela interferência alternadamente aditiva e subtrativa das frentes de onda. O experimento de Young, realizado no início dos anos 1800, desempenhou um papel crucial na compreensão da teoria ondulatória da luz, vencendo a teoria corpuscular da luz proposta por Isaac Newton, que havia sido o modelo aceito de propagação da luz no século XVII. e séculos XVIII. No entanto, a descoberta posterior do efeito fotoelétrico demonstrou que, em diferentes circunstâncias, a luz pode se comportar como se fosse composta de partículas discretas. Essas descobertas aparentemente contraditórias tornaram necessário ir além da física clássica e levar em consideração a natureza quântica da luz.

Feynman gostava de dizer que toda a mecânica quântica pode ser obtida pensando cuidadosamente nas implicações desse único experimento. Ele também propôs (como um experimento mental) que se os detectores fossem colocados antes de cada fenda, o padrão de interferência desapareceria.

A relação de dualidade Englert-Greenberger fornece um tratamento detalhado da matemática da interferência de fenda dupla no contexto da mecânica quântica.

Um experimento de fenda dupla de baixa intensidade foi realizado pela primeira vez por G. I. Taylor em 1909, reduzindo o nível de luz incidente até que os eventos de emissão/absorção de fótons não fossem sobrepostos. Um experimento de dupla fenda não foi realizado com nada além de luz até 1961, quando Claus Jönsson, da Universidade de Tübingen, o realizou com feixes de elétrons. Em 1974, os físicos italianos Pier Giorgio Merli, Gian Franco Missiroli e Giulio Pozzi repetiram o experimento usando elétrons únicos e biprismas (em vez de fendas), mostrando que cada elétron interfere consigo mesmo conforme previsto pela teoria quântica. Em 2002, a versão de um único elétron do experimento foi eleita "o experimento mais bonito" pelos leitores do Physics World.

Em 2012, Stefano Frabboni e seus colegas finalmente realizaram o experimento de dupla fenda com elétrons e fendas reais, seguindo o esquema original proposto por Feynman. Eles enviaram elétrons únicos para fendas nanofabricadas (cerca de 100 nm de largura) e, ao coletar os elétrons transmitidos com um detector de elétron único, eles puderam mostrar o acúmulo de um padrão de interferência de fenda dupla.

Em 2018, a interferência de partícula única foi demonstrada pela primeira vez para a antimatéria no Laboratório de Pósitrons (L-NESS, Politecnico di Milano) de Rafael Ferragut em Como (Itália), por um grupo liderado por Marco Giammarchi.

Variações do experimento

Interferência de partículas individuais

Construção de padrão de interferência de deteções de partículas individuais

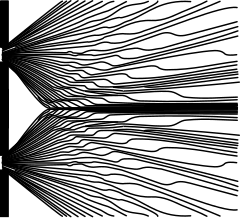
Uma versão importante deste experimento envolve partículas individuais. O envio de partículas através de um aparelho de fenda dupla, uma de cada vez, resulta no aparecimento de partículas únicas na tela, como esperado. Notavelmente, no entanto, um padrão de interferência surge quando essas partículas podem se acumular uma a uma (veja a imagem ao lado). Isso demonstra a dualidade onda-partícula, que afirma que toda matéria exibe propriedades de onda e partícula: a partícula é medida como um único pulso em uma única posição, enquanto a onda descreve a probabilidade de absorver a partícula em um local específico na tela. Foi demonstrado que esse fenômeno ocorre com fótons, elétrons, átomos e até mesmo algumas moléculas. O sucesso foi alcançado com buckminsterfulereno (C
₆₀) em 2001, com 2 moléculas de 430 átomos (C
₆₀(C
₁₂F
₂₅)
₁₀ e C
₁₆₈H
₉₄F
₁₅₂O
₈N
₄S
₄) em 2011 e com moléculas de até 2.000 átomos em 2019.

A probabilidade de detecção é o quadrado da amplitude da onda e pode ser calculada com ondas clássicas (veja abaixo). Desde a origem da mecânica quântica, alguns teóricos têm procurado maneiras de incorporar determinantes adicionais ou "variáveis ocultas" que, se fossem conhecidos, dariam conta da localização de cada impacto individual com o alvo.

Interferômetro de Mach-Zehnder

Os fótons em um interferômetro Mach-Zehnder exibem interferência semelhante a onda e detecção semelhante a partículas em detectores de fotos únicas.

O interferômetro Mach-Zehnder pode ser visto como uma versão simplificada do experimento de dupla fenda. Em vez de se propagar pelo espaço livre após as duas fendas e atingir qualquer posição em uma tela estendida, no interferômetro os fótons só podem se propagar por dois caminhos e atingir dois fotodetectores discretos. Isso torna possível descrevê-lo por meio de álgebra linear simples na dimensão 2, em vez de equações diferenciais.

Um fóton emitido pelo laser atinge o primeiro divisor de feixe e fica em uma superposição entre os dois caminhos possíveis. No segundo divisor de feixe, esses caminhos interferem, fazendo com que o fóton atinja o fotodetector à direita com probabilidade um e o fotodetector na parte inferior com probabilidade zero. É interessante considerar o que aconteceria se o fóton estivesse definitivamente em qualquer um dos caminhos entre os divisores de feixe. Isso pode ser feito bloqueando um dos caminhos ou, de forma equivalente, detectando a presença de um fóton ali. Em ambos os casos não haverá mais interferência entre os caminhos, e ambos os fotodetectores serão atingidos com probabilidade 1/2. A partir disso, podemos concluir que o fóton não segue um caminho ou outro após o primeiro divisor de feixe, mas sim que está em uma genuína superposição quântica dos dois caminhos.

"Para onde" experimentos e o princípio da complementaridade

Um conhecido experimento mental prevê que, se os detectores de partículas forem posicionados nas fendas, mostrando por qual fenda um fóton passa, o padrão de interferência desaparecerá. Essa experiência ilustra o princípio da complementaridade de que os fótons podem se comportar como partículas ou ondas, mas não podem ser observados como ambos ao mesmo tempo. Apesar da importância desse experimento mental na história da mecânica quântica (por exemplo, veja a discussão sobre a versão de Einstein desse experimento), realizações tecnicamente viáveis desse experimento não foram propostas até a década de 1970. (Implementações ingênuas do experimento mental do livro didático não são possíveis porque os fótons não podem ser detectados sem a absorção do fóton.) Atualmente, vários experimentos foram realizados ilustrando vários aspectos da complementaridade.

Um experimento realizado em 1987 produziu resultados que demonstraram que a informação poderia ser obtida sobre o caminho que uma partícula tomou sem destruir completamente a interferência. Isso mostrou o efeito das medições que perturbaram as partículas em trânsito em um grau menor e, portanto, influenciaram o padrão de interferência apenas em uma extensão comparável. Em outras palavras, se não insistirmos que o método usado para determinar por qual fenda cada fóton passa seja totalmente confiável, ainda assim podemos detectar um padrão de interferência (degradado).

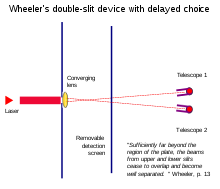
Escolha atrasada e variações de borracha quântica

Um diagrama do experimento de escolha tardia de Wheeler, mostrando o princípio de determinar o caminho do fóton depois de passar pela fenda

Os experimentos de escolha atrasada de Wheeler demonstram que extrair "qual caminho" a informação depois que uma partícula passa pelas fendas pode parecer alterar retroativamente seu comportamento anterior nas fendas.

Experiências de borracha quântica demonstram que o comportamento da onda pode ser restaurado apagando ou tornando permanentemente indisponível o "qual caminho" Informação.

Uma simples ilustração caseira do fenômeno do apagador quântico foi fornecida em um artigo da Scientific American. Se colocarmos polarizadores antes de cada fenda com seus eixos ortogonais entre si, o padrão de interferência será eliminado. Os polarizadores podem ser considerados como introduzindo informações de qual caminho para cada feixe. A introdução de um terceiro polarizador na frente do detector com um eixo de 45° em relação aos outros polarizadores "apaga" esta informação, permitindo que o padrão de interferência reapareça. Isso também pode ser explicado considerando a luz como uma onda clássica e também ao usar polarizadores circulares e fótons individuais. Implementações dos polarizadores usando pares de fótons emaranhados não têm explicação clássica.

Medição fraca

Em um experimento altamente divulgado em 2012, os pesquisadores afirmaram ter identificado o caminho que cada partícula havia seguido sem nenhum efeito adverso no padrão de interferência gerado pelas partículas. Para fazer isso, eles usaram uma configuração de modo que as partículas que chegam à tela não sejam de uma fonte pontual, mas de uma fonte com dois máximos de intensidade. No entanto, comentaristas como Svensson apontaram que, de fato, não há conflito entre as medições fracas realizadas nesta variante do experimento da fenda dupla e o princípio da incerteza de Heisenberg. A medição fraca seguida de pós-seleção não permitiu medições simultâneas de posição e momento para cada partícula individual, mas permitiu a medição da trajetória média das partículas que chegaram a diferentes posições. Em outras palavras, os pesquisadores estavam criando um mapa estatístico da paisagem de trajetória completa.

Outras variações

Um conjunto de dupla fenda de laboratório; distância entre os postos superiores aproximadamente 2,5 cm (um polegada).

Padrões de distribuição de intensidade de campo próximo para fendas plasmônicas com larguras iguais (A) e larguras não iguais (B).

Em 1967, Pfleegor e Mandel demonstraram interferência de duas fontes usando dois lasers separados como fontes de luz.

Foi demonstrado experimentalmente em 1972 que em um sistema de fenda dupla onde apenas uma fenda estava aberta a qualquer momento, a interferência foi observada, desde que a diferença de caminho fosse tal que o fóton detectado pudesse ter vindo de qualquer uma das fendas. As condições experimentais eram tais que a densidade de fótons no sistema era muito menor que a unidade.

Em 1999, um experimento de interferência quântica (usando uma grade de difração, em vez de duas fendas) foi realizado com sucesso com moléculas de buckyball (cada uma com 60 átomos de carbono). Uma buckyball é grande o suficiente (cerca de 0,7 nm de diâmetro, quase meio milhão de vezes maior que um próton) para ser vista em um microscópio eletrônico.

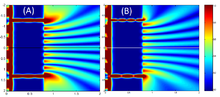
Em 2005, E. R. Eliel apresentou um estudo experimental e teórico da transmissão óptica de uma tela metálica fina perfurada por duas fendas de subcomprimento de onda, separadas por muitos comprimentos de onda ópticos. A intensidade total do padrão de dupla fenda de campo distante é reduzida ou aumentada em função do comprimento de onda do feixe de luz incidente.

Em 2012, pesquisadores da Universidade de Nebraska–Lincoln realizaram o experimento de dupla fenda com elétrons conforme descrito por Richard Feynman, usando novos instrumentos que permitiam o controle da transmissão das duas fendas e o monitoramento de eventos de detecção de elétron único. Os elétrons foram disparados por um canhão de elétrons e passaram por uma ou duas fendas de 62 nm de largura × 4 μm de altura.

Em 2013, um experimento de interferência quântica (usando redes de difração, em vez de duas fendas) foi realizado com sucesso com moléculas que compreendiam 810 átomos (cuja massa total era superior a 10.000 unidades de massa atômica). O recorde foi elevado para 2.000 átomos (25.000 amu) em 2019.

Análogos de onda piloto hidrodinâmica

Foram desenvolvidos análogos hidrodinâmicos que podem recriar vários aspectos dos sistemas mecânicos quânticos, incluindo interferência de partícula única através de uma fenda dupla. Uma gota de óleo de silicone, quicando ao longo da superfície de um líquido, se autopropulsiona por meio de interações ressonantes com seu próprio campo de onda. A gota espirra suavemente o líquido a cada salto. Ao mesmo tempo, ondulações de saltos anteriores afetam seu curso. A interação da gota com suas próprias ondulações, que formam o que é conhecido como onda piloto, faz com que ela exiba comportamentos anteriormente considerados peculiares às partículas elementares – incluindo comportamentos normalmente tomados como evidência de que partículas elementares estão espalhadas pelo espaço como ondas, sem localização específica, até que sejam medidas.

Comportamentos imitados através deste sistema hidrodinâmico de onda piloto incluem difração quântica de partícula única, tunelamento, órbitas quantizadas, divisão de nível orbital, spin e estatísticas multimodais. Também é possível inferir relações de incerteza e princípios de exclusão. Vídeos estão disponíveis ilustrando vários recursos deste sistema. (Veja os links externos.)

No entanto, sistemas mais complicados que envolvem duas ou mais partículas em superposição não são passíveis de uma explicação tão simples e classicamente intuitiva. Consequentemente, nenhum análogo hidrodinâmico de emaranhamento foi desenvolvido. No entanto, análogos ópticos são possíveis.

Formulação clássica de óptica de onda

Padrão de difração de duas fendas por uma onda de plano

Foto da interferência de duas fendas da luz solar.

Duas fendas são iluminadas por uma onda de avião.

Muito do comportamento da luz pode ser modelado usando a teoria clássica das ondas. O princípio Huygens-Fresnel é um desses modelos; afirma que cada ponto em uma frente de onda gera uma onda secundária e que a perturbação em qualquer ponto subsequente pode ser encontrada somando as contribuições das ondas individuais naquele ponto. Este somatório precisa levar em conta a fase, bem como a amplitude das ondas individuais. Apenas a intensidade de um campo de luz pode ser medida - isso é proporcional ao quadrado da amplitude.

No experimento de fenda dupla, as duas fendas são iluminadas pela luz quase monocromática de um único laser. Se a largura das fendas for pequena o suficiente (muito menor que o comprimento de onda da luz do laser), as fendas difratam a luz em ondas cilíndricas. Essas duas frentes de onda cilíndricas são sobrepostas e a amplitude e, portanto, a intensidade, em qualquer ponto das frentes de onda combinadas, depende tanto da magnitude quanto da fase das duas frentes de onda. A diferença de fase entre as duas ondas é determinada pela diferença na distância percorrida pelas duas ondas.

Se a distância de visualização for grande em comparação com a separação das fendas (o campo distante), a diferença de fase pode ser encontrada usando a geometria mostrada na figura abaixo à direita. A diferença de caminho entre duas ondas que viajam em um ângulo θ é dada por:

Dpecado⁡ ⁡ θ θ ? ? Dθ θ {displaystyle dsin theta approx dtheta }

Onde d é a distância entre as duas fendas. Quando as duas ondas estão em fase, ou seja, a diferença de caminho é igual a um número inteiro de comprimentos de onda, a amplitude somada e, portanto, a intensidade somada é máxima, e quando estão em antifase, ou seja, a diferença de caminho é igual à metade um comprimento de onda, um comprimento de onda e meio, etc., então as duas ondas se cancelam e a intensidade somada é zero. Este efeito é conhecido como interferência. Os máximos da franja de interferência ocorrem em ângulos

Dθ θ n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =nλ λ ,n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,1,2,...... _{n}=nlambda~n=0,1,2,ldots }

onde λ é o comprimento de onda da luz. O espaçamento angular das franjas, θ_f, é dado por

θ θ f? ? λ λ /D{displaystyle theta _{f}approx lambda /d}

O espaçamento das franjas a uma distância z das fendas é dado por

O quê?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =zangão.θ θ f= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =zangão.λ λ /D- Sim. _{f=zlambda Não.

Por exemplo, se duas fendas estiverem separadas por 0,5 mm (d) e forem iluminadas com um laser de comprimento de onda de 0,6 μm (λ), então a uma distância de 1 m (z), o espaçamento das franjas será de 1,2 milímetros.

Se a largura das fendas b for apreciável em comparação com o comprimento de onda, a equação de difração de Fraunhofer é necessária para determinar a intensidade da luz difratada do seguinte modo:

Eu...(θ θ )∝ ∝ e2⁡ ⁡ Não.D D Dpecado⁡ ⁡ θ θ λ λ ]SEu...nc2Não.D D b)pecado⁡ ⁡ θ θ λ λ ]{displaystyle {begin{aligned}I(theta)&propto cos ^{2}left[{frac - Sim. }{lambda }}right]~mathrm {sinc} ^{2}left[{frac {pi bsin theta }{lambda }}right]end{aligned}}}

onde a função sinc é definida como sinc(x) = sin(x)/x para x ≠ 0, e sinc(0) = 1.

Isto é ilustrado na figura acima, onde o primeiro padrão é o padrão de difração de uma única fenda, dado pela função sinc nesta equação, e a segunda figura mostra a intensidade combinada da luz difratada das duas fendas, onde a função cos representa a estrutura fina, e a estrutura mais grosseira representa a difração pelas fendas individuais conforme descrito pela classe sinc.

Cálculos semelhantes para o campo próximo podem ser feitos aplicando a equação de difração de Fresnel, o que implica que, à medida que o plano de observação se aproxima do plano em que as fendas estão localizadas, os padrões de difração associados a cada fenda diminuem de tamanho, de modo que a área em que ocorre a interferência seja reduzida e possa desaparecer completamente quando não houver sobreposição nos dois padrões difratados.

Interpretações do experimento

Assim como o experimento mental do gato de Schrödinger, o experimento da dupla fenda é frequentemente usado para destacar as diferenças e semelhanças entre as várias interpretações da mecânica quântica.

Interpretação de Copenhague

A interpretação de Copenhague, apresentada por alguns dos pioneiros no campo da mecânica quântica, afirma que é indesejável postular qualquer coisa que vá além das fórmulas matemáticas e dos tipos de aparatos e reações físicas que nos permitem obter algum conhecimento do que acontece na escala atômica. Uma das construções matemáticas que permite aos experimentadores prever com muita precisão certos resultados experimentais é às vezes chamada de onda de probabilidade. Em sua forma matemática, é análogo à descrição de uma onda física, mas suas "cristas" e "depressas" indicam níveis de probabilidade para a ocorrência de certos fenômenos (por exemplo, uma centelha de luz em um determinado ponto na tela do detector) que podem ser observados no mundo macro da experiência humana comum.

A "onda" pode-se dizer que "passa pelo espaço" porque os valores de probabilidade que se podem calcular a partir de sua representação matemática dependem do tempo. Não se pode falar da localização de qualquer partícula, como um fóton, entre o momento em que é emitido e o momento em que é detectado, simplesmente porque, para dizer que algo está localizado em algum lugar em um determinado momento, é preciso detectá-lo. O requisito para o eventual aparecimento de um padrão de interferência é que as partículas sejam emitidas e que haja uma tela com pelo menos dois caminhos distintos para a partícula seguir do emissor até a tela de detecção. Os experimentos não observam absolutamente nada entre o tempo de emissão da partícula e sua chegada na tela de detecção. Se um traçado de raio for feito em seguida como se uma onda de luz (como entendida na física clássica) fosse larga o suficiente para seguir ambos os caminhos, então esse traçado de raio preveria com precisão o aparecimento de máximos e mínimos na tela do detector quando muitas partículas passarem pelo aparelho e gradualmente "pintar" o padrão de interferência esperado.

Formulação de integral de caminho

Um de um número infinito de caminhos igualmente prováveis usados na integral do caminho de Feynman (veja também: processo Wiener)

A interpretação de Copenhague é semelhante à formulação do caminho integral da mecânica quântica fornecida por Feynman. A formulação do caminho integral substitui a noção clássica de uma trajetória única e única para um sistema, com uma soma de todas as trajetórias possíveis. As trajetórias são somadas usando a integração funcional.

Cada caminho é considerado igualmente provável e, portanto, contribui com a mesma quantia. No entanto, a fase dessa contribuição em qualquer ponto ao longo do caminho é determinada pela ação ao longo do caminho:

Acaminho(x,Sim.,zangão.,))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =eEu...S(x,Sim.,zangão.,))(x,y,z,t)=e^{iS(x,y,z,t)}}

Todas essas contribuições são então somadas e a magnitude do resultado final é elevada ao quadrado, para obter a distribuição de probabilidade para a posição de uma partícula:

p(x,Sim.,zangão.,))∝ ∝ |∫ ∫ todos os caminhoseEu...S(x,Sim.,zangão.,))|2{displaystyle p(x,y,z,t)propto leftvert int _{text{all paths}}e^{iS(x,y,z,t)}rightvert ^{2}}

Como sempre acontece ao calcular a probabilidade, os resultados devem ser normalizados impondo:

∫ ∫ ∫ ∫ todo o espaçop(x,Sim.,zangão.,))DV= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1{displaystyle iiint _{text{all space}}p(x,y,z,t),dV=1}

Para resumir, a distribuição de probabilidade do resultado é o quadrado normalizado da norma da superposição, sobre todos os caminhos desde o ponto de origem até o ponto final, de ondas que se propagam proporcionalmente à ação ao longo de cada caminho. As diferenças na ação cumulativa ao longo dos diferentes caminhos (e, portanto, as fases relativas das contribuições) produzem o padrão de interferência observado pelo experimento da dupla fenda. Feynman enfatizou que sua formulação é apenas uma descrição matemática, não uma tentativa de descrever um processo real que podemos medir.

Interpretação relacional

Um exemplo do princípio de incerteza relacionado à interpretação relacional. Quanto mais se sabe sobre a posição de uma partícula, menos se sabe sobre a velocidade, e vice-versa

De acordo com a interpretação relacional da mecânica quântica, proposta pela primeira vez por Carlo Rovelli, observações como as do experimento da dupla fenda resultam especificamente da interação entre o observador (aparelho de medição) e o objeto observado (com o qual interage fisicamente), não qualquer propriedade absoluta possuída pelo objeto. No caso de um elétron, se ele for inicialmente "observado" em uma fenda particular, então a interação observador-partícula (fóton-elétron) inclui informações sobre a posição do elétron. Isso restringe parcialmente a eventual localização da partícula na tela. Se for "observado" (medido com um fóton) não em uma fenda específica, mas sim na tela, então não há "qual caminho" informações como parte da interação, de modo que o elétron "observado" posição na tela é determinada estritamente por sua função de probabilidade. Isso torna o padrão resultante na tela o mesmo como se cada elétron individual tivesse passado por ambas as fendas.

Interpretação de muitos mundos

O físico David Deutsch argumenta em seu livro The Fabric of Reality que o experimento da dupla fenda é evidência para a interpretação de muitos mundos. No entanto, como toda interpretação da mecânica quântica é empiricamente indistinguível, alguns cientistas são céticos em relação a essa afirmação.

Teoria de De Broglie-Bohm

Uma alternativa para a compreensão padrão da mecânica quântica, a teoria De Broglie-Bohm afirma que as partículas também têm localizações precisas em todos os momentos e que suas velocidades são definidas pela função de onda. Assim, embora uma única partícula viaje por uma fenda específica no experimento de fenda dupla, a chamada "onda piloto" que o influencia passará por ambos. As trajetórias de duas fendas de Broglie-Bohm foram calculadas pela primeira vez por Chris Dewdney enquanto trabalhava com Chris Philippidis e Basil Hiley no Birkbeck College (Londres). A teoria de Broglie-Bohm produz os mesmos resultados estatísticos que a mecânica quântica padrão, mas dispensa muitas de suas dificuldades conceituais.

Trajeções da Boémia

Trajetórios de partículas sob a teoria de De Broglie-Bohm na experiência de dupla fenda.

100 trajetórias guiadas pela função de onda. Na teoria de De Broglie-Bohm, uma partícula é representada, a qualquer momento, por uma função de onda e uma posição (centro de massa). Este é um tipo de realidade aumentada em comparação com a interpretação padrão.

Simulação numérica do experimento de dupla fenda com elétrons. Figura à esquerda: evolução (da esquerda para a direita) da intensidade do feixe de elétrons na saída das fendas (esquerda) até a tela de detecção localizada 10cm após as fendas (direita). Quanto maior a intensidade, mais a cor é azul claro - Figura no centro: impactos dos elétrons observados na tela - Figura à direita: intensidade dos elétrons na aproximação de campo distante (na tela). Dados numéricos da experiência de Claus Jönsson (1961). Fotões, átomos e moléculas seguem uma evolução semelhante.