Estatística inferencial

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

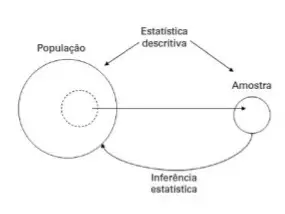
A inferência estatística ou estatística inferencial é o processo de usar a análise de dados para inferir propriedades de uma distribuição de probabilidade subjacente. A análise estatística inferencial infere propriedades de uma população, por exemplo, testando hipóteses e derivando estimativas. Supõe-se que o conjunto de dados observados seja extraído de uma população maior.

A estatística inferencial pode ser contrastada com a estatística descritiva. A estatística descritiva lida apenas com as propriedades dos dados observados e não se baseia na suposição de que os dados provêm de uma população maior. No aprendizado de máquina, o termo inferência às vezes é usado para significar "fazer uma previsão, avaliar um modelo já treinado"; nesse contexto, a inferência das propriedades do modelo é chamada de treinamento ou aprendizado (ao invés de inferência), e o uso de um modelo para predição é chamado de inferência (ao invés de previsão); veja também inferência preditiva.

Introdução

A inferência estatística faz proposições sobre uma população, usando dados extraídos da população com alguma forma de amostragem. Dada uma hipótese sobre uma população para a qual desejamos fazer inferências, a inferência estatística consiste em (primeiro) selecionar um modelo estatístico do processo que gera os dados e (segundo) derivar proposições do modelo.

Konishi e Kitagawa afirmam que "a maioria dos problemas de inferência estatística podem ser considerados problemas relacionados à modelagem estatística". A esse respeito, Sir David Cox disse: "A maneira pela qual [a] tradução do problema da matéria para o modelo estatístico é feita é muitas vezes a parte mais crítica de uma análise".

A conclusão de uma inferência estatística é uma afirmação estatística. Algumas formas comuns de proposição estatística são as seguintes:

uma estimativa pontual, ou seja, um valor particular que melhor se aproxime de algum parâmetro de interesse;
uma estimativa de intervalo, por exemplo, um intervalo de confiança (ou uma estimativa de conjunto), ou seja, um intervalo construído usando um conjunto de dados extraído de uma população de modo que, em amostragem repetida dos referidos conjuntos de dados, os referidos intervalos contenham o valor verdadeiro de o parâmetro com a probabilidade no nível de confiança estabelecido;
um intervalo credível, ou seja, um conjunto de valores contendo, por exemplo, 95% da crença posterior;
rejeição de uma hipótese;
agrupar ou classificar os pontos de dados em grupos.

Modelos e suposições

Qualquer inferência estatística requer algumas suposições. Um modelo estatístico é um conjunto de suposições relacionadas à geração dos dados observados e similares. Descrições de modelos estatísticos muitas vezes enfatizam o papel das grandezas populacionais de interesse, sobre as quais desejamos fazer inferências. As estatísticas descritivas são normalmente usadas como uma etapa preliminar antes de se fazer inferências mais formais.

Grau de modelos/suposições

Os estatísticos distinguem entre três níveis de suposições de modelagem;

Totalmente paramétrico – As distribuições de probabilidade que descrevem o processo de geração de dados são consideradas totalmente descritas por uma família de distribuições de probabilidade envolvendo apenas um número finito de parâmetros desconhecidos. Por exemplo, pode-se supor que a distribuição de valores na população seja verdadeiramente Normal, com média e variância desconhecidas, e que os conjuntos de dados sejam gerados por amostragem aleatória "simples". A família de modelos lineares generalizados é uma classe flexível e amplamente utilizada de modelos paramétricos.
Não paramétrico – As suposições sobre o processo que gera os dados são muito menores do que nas estatísticas paramétricas e podem ser mínimas. Por exemplo, toda distribuição de probabilidade contínua possui uma mediana, que pode ser estimada usando a mediana amostral ou o estimador Hodges-Lehmann-Sen, que possui boas propriedades quando os dados são provenientes de amostragem aleatória simples.
Semi-paramétrico : Este termo normalmente implica suposições "intermediárias" abordagens completas e não paramétricas. Por exemplo, uma distribuição populacional pode ser assumida como tendo uma média finita. Além disso, pode-se supor que o nível médio de resposta na população depende de forma verdadeiramente linear de alguma covariável (uma suposição paramétrica), mas não fazer suposições paramétricas descrevendo a variância em torno dessa média (ou seja, na presença ou forma possível de qualquer heterocedasticidade). De maneira mais geral, os modelos semiparamétricos geralmente podem ser separados em componentes "estruturais" e de "variação aleatória". Um componente é tratado parametricamente e o outro não parametricamente.

Importância de modelos/suposições válidas

Qualquer que seja o nível de suposição, a inferência adequadamente calibrada geralmente requer que essas suposições estejam corretas; ou seja, que os mecanismos de geração de dados foram realmente especificados corretamente.

Suposições incorretas de amostragem aleatória "simples" podem invalidar a inferência estatística. Suposições semi-paramétricas e totalmente paramétricas mais complexas também são motivo de preocupação. Por exemplo, assumir incorretamente o modelo de Cox pode, em alguns casos, levar a conclusões errôneas. Suposições incorretas de normalidade populacional também invalidam algumas formas de inferência baseada em regressão. O uso de qualquer O modelo paramétrico é visto com ceticismo pela maioria dos especialistas em amostragem da população humana: "a maioria das estatísticas de amostragem, quando lidam com intervalos de confiança, limitam-se a declarações sobre [estimadores] com base em amostras muito grandes". que esses [estimadores] terão distribuições que são quase normais." Em particular, uma distribuição normal "seria uma suposição totalmente irrealista e catastroficamente imprudente se estivéssemos lidando com qualquer tipo de população econômica". Aqui, o teorema do limite central afirma que a distribuição da média amostral "para amostras muito grandes" tem uma distribuição aproximadamente normal, se a distribuição não for de cauda pesada.

Distribuições aproximadas

Dada a dificuldade de especificar distribuições exatas das estatísticas amostrais, muitos métodos foram desenvolvidos para aproximá-las.

Com amostras finitas, os resultados de aproximação medem o quanto uma distribuição limitante se aproxima da distribuição amostral da estatística: por exemplo, com 10.000 amostras independentes, a distribuição normal aproxima (com dois dígitos de precisão) a distribuição da amostra média para muitas distribuições populacionais, pelo método de Berry – Teorema de Esseen. No entanto, para muitos propósitos práticos, a aproximação normal fornece uma boa aproximação da distribuição da média amostral quando há 10 (ou mais) amostras independentes, dependendo dos estudos de simulação e da experiência dos estatísticos. Seguindo o trabalho de Kolmogorov na década de 1950, a estatística avançada usa teoria de aproximação e análise funcional para quantificar o erro de aproximação. Nesta abordagem, estuda-se a geometria métrica das distribuições de probabilidade; essa abordagem quantifica o erro de aproximação com, por exemplo, a divergência de Kullback-Leibler, a divergência de Bregman e a distância de Hellinger.

Com amostras indefinidamente grandes, resultados limitantes, como o teorema do limite central, descrevem a distribuição limite da estatística amostral, se existir. Os resultados limitantes não são declarações sobre amostras finitas e, de fato, são irrelevantes para amostras finitas. No entanto, a teoria assintótica de distribuições limitantes é frequentemente invocada para trabalhar com amostras finitas. Por exemplo, resultados limitantes são frequentemente invocados para justificar o método generalizado de momentos e o uso de equações de estimativa generalizada, que são populares em econometria e bioestatística. A magnitude da diferença entre a distribuição limite e a distribuição verdadeira (formalmente, o "erro" da aproximação) pode ser avaliada por simulação.

Modelos baseados em randomização

Para um determinado conjunto de dados que foi produzido por um projeto de randomização, a distribuição de randomização de uma estatística (sob a hipótese nula) é definida avaliando a estatística de teste para todos os planos que poderiam ter sido gerados pelo projeto de randomização. Na inferência frequentista, a randomização permite que as inferências sejam baseadas na distribuição de randomização em vez de um modelo subjetivo, e isso é especialmente importante na amostragem de pesquisas e no projeto de experimentos. A inferência estatística a partir de estudos randomizados também é mais simples do que muitas outras situações.Na inferência bayesiana, a randomização também é importante: na amostragem por inquérito, o uso de amostragem sem reposição garante a intercambialidade da amostra com a população;

A randomização objetiva permite procedimentos adequadamente indutivos. Muitos estatísticos preferem análises baseadas em randomização de dados que foram gerados por procedimentos de randomização bem definidos. (No entanto, é verdade que em campos da ciência com insights teóricos desenvolvidos e controle experimental, experimentos aleatórios podem aumentar os custos da experimentação sem melhorar a qualidade das inferências.) Da mesma forma, as principais autoridades estatísticas recomendam os resultados de experimentos aleatórios como permitindo inferências com maior confiabilidade do que estudos observacionais dos mesmos fenômenos. No entanto, um bom estudo observacional pode ser melhor do que um experimento aleatório ruim.

A análise estatística de um experimento randomizado pode ser baseada no esquema de randomização estabelecido no protocolo experimental e não requer um modelo subjetivo.1

No entanto, em qualquer momento, algumas hipóteses não podem ser testadas usando modelos estatísticos objetivos, que descrevem com precisão experimentos aleatórios ou amostras aleatórias. Em alguns casos, esses estudos randomizados são um desperdício ou antiéticos.

Análise Baseada em Modelos de Experimentos Randomizados

É prática padrão referir-se a um modelo estatístico, por exemplo, um modelo linear ou logístico, ao analisar dados de experimentos aleatórios. No entanto, o esquema de randomização orienta a escolha de um modelo estatístico. Não é possível escolher um modelo adequado sem conhecer o esquema de randomização. Resultados seriamente enganosos podem ser obtidos analisando dados de experimentos aleatórios ignorando o protocolo experimental; Erros comuns incluem esquecer o bloqueio usado em um experimento e confundir medições repetidas na mesma unidade experimental com réplicas independentes do tratamento aplicado a diferentes unidades experimentais.

Inferência de randomização sem modelo

As técnicas livres de modelos complementam os métodos baseados em modelos, que empregam estratégias reducionistas de simplificação da realidade. Os primeiros combinam, evoluem, montam e treinam algoritmos adaptando-se dinamicamente às afinidades contextuais de um processo e aprendendo as características intrínsecas das observações.

Por exemplo, a regressão linear simples sem um modelo é baseada em

um desenho aleatório, onde os pares de observações $(X_{1},Y_{1}),(X_{2},Y_{2}),\cdots,(X_{n},Y_{n})$ são independentes e identicamente distribuídos (iid), ou
um desenho determinístico, onde as variáveis $X_{1},X_{2},\cdots ,X_{n}$ são determinísticas, mas as variáveis de resposta correspondentes $Y_{1},Y_{2},\cdots,Y_{n}$ são aleatórias e independentes com uma distribuição condicional comum, ou seja, $P\left(Y_{j}\leq y |X_{j}=x\right)=D_{x}(y)$ , que é independente do índice $j$ .

Em qualquer caso, a inferência de randomização sem modelo para as características da distribuição condicional comum ${\estilo de exibição D_{x}(.)}$ é baseada em algumas condições de regularidade, por exemplo, suavidade funcional. Por exemplo, a inferência de randomização sem modelo para a população característica média condicional, ${\ estilo de exibição \mu(x)=E(Y|X=x)}$ , pode ser consistentemente estimada por uma média local ou um ajuste polinomial local, sob a suposição de que $\mu(x)$ é suave. Além disso, com base na normalidade assintótica ou reamostragem, podemos construir intervalos de confiança para a característica da população, neste caso a média condicional, $\mu(x)$ .

Paradigmas de inferência

Diferentes escolas de inferência estatística foram estabelecidas. Essas escolas, ou "paradigmas", não são mutuamente exclusivas, e os métodos que funcionam bem sob um paradigma geralmente têm interpretações atraentes sob outros paradigmas.

Bandyopadhyay e Forster descrevem quatro paradigmas: "(i) estatística clássica ou estatística de erro, (ii) estatística Bayesiana, (iii) estatística baseada em probabilidade e (iv) estatística baseada em critério de informação Akaikeana". O paradigma clássico (ou frequentista), o paradigma bayesiano, o paradigma plausível e o paradigma baseado em AIC estão resumidos abaixo.

inferência frequentista

Esse paradigma calibra a plausibilidade das proposições considerando (teórica) amostragem repetida de uma distribuição populacional para produzir conjuntos de dados semelhantes ao que temos em mãos. Ao considerar as características do conjunto de dados em amostragem repetida, as propriedades freqüentistas de uma proposta estatística podem ser quantificadas, embora na prática essa quantificação possa ser desafiadora.

Exemplos de inferência frequentista

valor p
Intervalo de confiança
Teste de significância de hipótese nula

Inferência frequente, objetividade e teoria da decisão

Uma interpretação da inferência frequentista (ou inferência clássica) é que ela é aplicável apenas em termos de probabilidade de frequência; isto é, em termos de amostragem repetida de uma população. No entanto, a abordagem de Neyman desenvolve esses procedimentos em termos de probabilidades anteriores ao experimento. Ou seja, antes de realizar um experimento, decide-se sobre uma regra para chegar a uma conclusão tal que a probabilidade de ser correta seja adequadamente controlada: tal probabilidade não precisa ter uma amostragem repetida ou interpretação freqüentista. Em contraste, a inferência Bayesiana funciona em termos de probabilidades condicionais (ou seja, probabilidades condicionais aos dados observados),

Testes de significância freqüentes e procedimentos de intervalo de confiança podem ser construídos sem levar em consideração as funções de utilidade. No entanto, alguns elementos da estatística frequentista, como a teoria da decisão estatística, incorporam funções de utilidade. Em particular, desenvolvimentos freqüentistas de inferência ótima (como estimadores imparciais de menor variância ou testes uniformemente mais poderosos) fazem uso de funções de perda, que desempenham o papel de funções de utilidade (negativas). As funções de perda não precisam ser declaradas explicitamente para os teóricos estatísticos mostrarem que um procedimento estatístico tem uma propriedade de otimalidade. No entanto, as funções de perda geralmente são úteis para definir propriedades de otimização: por exemplo,

Enquanto os estatísticos que usam inferência frequentista devem escolher os parâmetros de interesse e os estimadores/estatísticas de teste a serem usados, a ausência de utilidades obviamente explícitas e distribuições anteriores ajudou os procedimentos frequentistas a serem amplamente considerados 'objetivos'.

Inferência Bayesiana

O cálculo bayesiano descreve graus de crença usando a "linguagem" da probabilidade; as crenças são positivas, estão integradas em uma e obedecem aos axiomas da probabilidade. A inferência bayesiana usa crenças posteriores disponíveis como base para fazer proposições estatísticas. Existem várias justificativas diferentes para usar a abordagem Bayesiana.

Exemplos de inferência bayesiana

Intervalo confiável para estimativa de intervalo
Fatores de Bayes para comparação de modelos

Inferência Bayesiana, Subjetividade e Teoria da Decisão

Muitas inferências Bayesianas informais são baseadas em resumos "intuitivamente razoáveis" da posterior. Por exemplo, média posterior, mediana e moda, intervalos de densidade posterior mais altos e fatores de Bayes podem ser motivados dessa maneira. Embora não seja necessário declarar a função de utilidade de um usuário para esse tipo de inferência, todos esses resumos dependem (até certo ponto) de crenças anteriores e são geralmente considerados conclusões subjetivas. (Métodos de pré-construção que não requerem entrada externa foram propostos, mas ainda não foram totalmente desenvolvidos.)

Formalmente, a inferência Bayesiana é calibrada com referência a uma utilidade ou função de perda explicitamente declarada; a 'regra de Bayes' é aquela que maximiza a utilidade esperada, calculada sobre a incerteza posterior. Assim, a inferência Bayesiana formal produz automaticamente decisões ótimas no sentido teórico da decisão. Dadas as suposições, os dados e a utilidade, a inferência bayesiana pode ser realizada para praticamente qualquer problema, embora nem todas as inferências estatísticas precisem de uma interpretação bayesiana. As análises que não são formalmente Bayesianas podem ser (logicamente) inconsistentes; uma característica dos procedimentos Bayesianos que usam priores apropriados (isto é, aqueles integráveis a um) é que eles são garantidos para serem consistentes. deve ocorrer neste quadro teórico de decisão, e que a inferência Bayesiana não deve terminar com a avaliação e resumo de crenças subsequentes.

Inferência baseada em probabilidade

A probabilidade aborda as estatísticas usando a função de verossimilhança. Alguns verossimistas rejeitam a inferência, considerando as estatísticas apenas como suporte computacional da evidência. Outros, porém, propõem inferências baseadas na função de verossimilhança, sendo a mais conhecida a estimativa de máxima verossimilhança.

Inferência baseada em AIC

O Critério de Informação de Akaike (AIC) é um estimador da qualidade relativa de modelos estatísticos para um determinado conjunto de dados. Dada uma coleção de modelos para os dados, o AIC estima a qualidade de cada modelo em relação a cada um dos outros modelos. Assim, o AIC fornece um meio para a seleção do modelo.

O AIC é baseado na teoria da informação: fornece uma estimativa da informação relativa perdida quando um determinado modelo é usado para representar o processo que gerou os dados. (Ao fazer isso, ele lida com o trade-off entre a qualidade do ajuste do modelo e a simplicidade do modelo.)

Outros paradigmas para inferência

Comprimento mínimo da descrição

O princípio do comprimento mínimo de descrição (MDL) foi desenvolvido a partir de ideias da teoria da informação e da teoria da complexidade de Kolmogorov. O princípio (MDL) seleciona modelos estatísticos que comprimem os dados o máximo possível; A inferência prossegue sem assumir "mecanismos geradores de dados" ou modelos de probabilidade não falsificáveis ou contrafactuais para os dados, como pode ser feito nas abordagens freqüentistas ou bayesianas.

No entanto, se um "mecanismo de geração de dados" realmente existe, então, de acordo com o teorema de codificação de origem de Shannon, ele fornece a descrição MDL dos dados, em média e assintoticamente. Ao minimizar o comprimento da descrição (ou complexidade descritiva), a estimativa MDL é semelhante à estimativa de máxima verossimilhança e à estimativa posterior máxima (usando priores Bayesianas de máxima entropia). No entanto, o MDL evita assumir que o modelo de probabilidade subjacente é conhecido; O princípio do MDL também pode ser aplicado sem assumir que, por exemplo, os dados provêm de amostragem independente.

O princípio MDL tem sido aplicado na teoria de codificação de comunicação, teoria da informação, regressão linear e mineração de dados.

A avaliação de procedimentos inferenciais baseados em MDL muitas vezes utiliza técnicas ou critérios da teoria da complexidade computacional.

inferência fiduciária

A inferência fiducial foi uma abordagem de inferência estatística baseada na probabilidade fiducial, também conhecida como "distribuição fiducial". Em trabalhos subsequentes, essa abordagem foi descrita como mal definida, extremamente limitada em aplicabilidade e até mesmo falaciosa. No entanto, esse argumento é o mesmo que mostrar que a chamada distribuição de confiança não é uma distribuição de probabilidade válida e, como isso não invalidou a aplicação dos intervalos de confiança, não necessariamente invalida as conclusões extraídas dos argumentos fiduciais. Foi feita uma tentativa de reinterpretar os primeiros trabalhos de Fisher sobre o argumento fiducial como um caso especial de uma teoria de inferência usando probabilidades superiores e inferiores.

Inferência estrutural

Com base nas idéias de Fisher e Pitman de 1938 a 1939, George A. Barnard desenvolveu "inferência estrutural" ou "inferência fundamental", uma abordagem que usa probabilidades invariáveis em famílias de grupos. Barnard reformulou os argumentos por trás da inferência fiducial sobre uma classe restrita de modelos em que os procedimentos "fiduciais" seriam bem definidos e úteis. Donald AS Fraser desenvolveu uma teoria geral para inferência estrutural baseada na teoria de grupos e a aplicou a modelos lineares. A teoria formulada por Fraser tem ligações estreitas com a teoria da decisão e estatísticas Bayesianas e pode fornecer regras de decisão freqüentistas ótimas se existirem.

Tópicos de inferência

Os tópicos abaixo geralmente se enquadram na área de inferência estatística.

Suposições estatísticas
Teoria da decisão estatística
Teoria da estimativa
Teste de hipótese estatística
Revisão de opiniões em estatísticas
Desenho de experimentos, análise de variância e regressão.
Amostragem de Pesquisa
Resumindo Dados Estatísticos

Contenido relacionado

Más resultados...