Efeito Borboleta
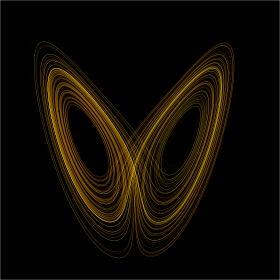
Na teoria do caos, o efeito borboleta é a dependência sensível das condições iniciais em que uma pequena mudança em um estado de um sistema não linear determinístico pode resultar em grandes diferenças em um estado posterior.
O termo está intimamente associado ao trabalho do matemático e meteorologista Edward Norton Lorenz. Ele observou que o efeito borboleta é derivado do exemplo metafórico dos detalhes de um tornado (o tempo exato de formação, o caminho exato percorrido) sendo influenciado por pequenas perturbações, como uma borboleta distante batendo suas asas várias semanas antes. Lorenz originalmente usou uma gaivota causando uma tempestade, mas foi persuadido a torná-la mais poética com o uso de borboletas e tornados em 1972. Ele descobriu o efeito quando observou execuções de seu modelo meteorológico com dados de condição inicial que foram arredondados de maneira aparentemente inconseqüente.. Ele notou que o modelo meteorológico falharia em reproduzir os resultados das execuções com os dados de condição inicial não arredondados. Uma mudança muito pequena nas condições iniciais criou um resultado significativamente diferente.
A ideia de que pequenas causas podem ter grandes efeitos no clima foi reconhecida anteriormente pelo matemático e engenheiro francês Henri Poincaré. O matemático e filósofo americano Norbert Wiener também contribuiu para essa teoria. O trabalho de Lorenz colocou o conceito de instabilidade da atmosfera terrestre em uma base quantitativa e ligou o conceito de instabilidade às propriedades de grandes classes de sistemas dinâmicos que estão passando por dinâmica não linear e caos determinístico.
Desde então, o conceito de efeito borboleta tem sido usado fora do contexto da ciência meteorológica como um termo amplo para qualquer situação em que uma pequena mudança é considerada a causa de consequências maiores.
História
Em The Vocation of Man (1800), Johann Gottlieb Fichte diz "você não poderia remover um único grão de areia de seu lugar sem com isso... mudar algo em todas as partes do o todo imensurável".
A teoria do caos e a dependência sensível das condições iniciais foram descritas em várias formas de literatura. Isso é evidenciado pelo caso do problema dos três corpos de Poincaré em 1890. Mais tarde, ele propôs que tais fenômenos poderiam ser comuns, por exemplo, na meteorologia.
Em 1898, Jacques Hadamard observou divergência geral de trajetórias em espaços de curvatura negativa. Pierre Duhem discutiu o possível significado geral disso em 1908.
Em 1950, Alan Turing observou: "O deslocamento de um único elétron por um bilionésimo de centímetro em um momento pode fazer a diferença entre um homem ser morto por uma avalanche um ano depois, ou escapar.&# 34;
A ideia de que a morte de uma borboleta poderia eventualmente ter um efeito cascata de longo alcance em eventos históricos subsequentes fez sua primeira aparição conhecida em "A Sound of Thunder", um conto de 1952 de Ray Bradbury. "Um Som de Trovão" apresenta viagem no tempo.
Mais precisamente, porém, a ideia quase exata e a frase exata - da asa de um minúsculo inseto afetando os ventos da atmosfera inteira - foi publicada em um livro infantil que se tornou extremamente bem-sucedido e conhecido mundialmente em 1962, um ano antes de Lorenz publicar:
"...o que quer que façamos afeta tudo e todos os outros, se mesmo da maneira mais pequena. Porque, quando uma mosca de casa bate nas asas, uma brisa vai ao redor do mundo."
- A Princesa da Razão Pura
—Norton Juster, O Tollbooth Fantasma
Em 1961, Lorenz estava executando um modelo de computador numérico para refazer uma previsão do tempo no meio da execução anterior como um atalho. Ele inseriu a condição inicial 0,506 da impressão em vez de inserir o valor de precisão total 0,506127. O resultado foi um cenário climático completamente diferente.
Lorens escreveu:
Em um ponto eu decidi repetir algumas das computações para examinar o que estava acontecendo em maior detalhe. Eu parei o computador, digitei em uma linha de números que tinha impresso fora um tempo antes, e defini-lo correndo novamente. Eu fui pelo corredor por uma xícara de café e voltei depois de cerca de uma hora, durante o qual o computador tinha simulado cerca de dois meses de tempo. Os números que estão sendo impressos não eram nada como os antigos. Eu imediatamente suspeitava de um tubo de vácuo fraco ou algum outro problema de computador, que não era incomum, mas antes de pedir o serviço eu decidi ver exatamente onde o erro ocorreu, sabendo que isso poderia acelerar o processo de manutenção. Em vez de uma ruptura súbita, descobri que os novos valores no início repetiram os antigos, mas logo depois diferiram por um e, em seguida, várias unidades no último lugar [decimal], e então começou a diferir no próximo ao último lugar e, em seguida, no lugar antes disso. Na verdade, as diferenças mais ou menos firmemente dobraram em tamanho a cada quatro dias ou assim, até que toda semelhança com a saída original desapareceu em algum lugar no segundo mês. Isso foi suficiente para me dizer o que tinha acontecido: os números que eu tinha digitado não foram os números originais exatos, mas foram os valores arredondados que tinham aparecido na impressão original. Os erros iniciais de round-off foram os culpados; eles estavam constantemente amplificando até que dominassem a solução.
—E. N. Lorenz, A essência do caos, U. Washington Press, Seattle (1993), página 134
Em 1963, Lorenz publicou um estudo teórico desse efeito em um artigo seminal altamente citado chamado Deterministic Nonperiodic Flow (os cálculos foram realizados em um computador Royal McBee LGP-30). Em outro lugar ele afirmou:
Um meteorologista observou que se a teoria estivesse correta, um retalho de asas de um gaivota do mar seria suficiente para alterar o curso do tempo para sempre. A controvérsia ainda não foi resolvida, mas a evidência mais recente parece favorecer as gaivotas do mar.
Seguindo propostas de colegas, em discursos e trabalhos posteriores, Lorenz usou a borboleta mais poética. Segundo Lorenz, ao não fornecer o título de uma palestra que apresentaria no 139º encontro da Associação Americana para o Avanço da Ciência, em 1972, Philip Merilees inventou O bater de asas de uma borboleta no Brasil define fora de um tornado no Texas? como título. Embora o bater de asas de uma borboleta tenha permanecido constante na expressão desse conceito, a localização da borboleta, as consequências e a localização das consequências variaram muito.
A frase refere-se à ideia de que as asas de uma borboleta podem criar pequenas mudanças na atmosfera que podem alterar o curso de um tornado ou retardar, acelerar ou até impedir a ocorrência de um tornado em outro local. A borboleta não alimenta ou cria diretamente o tornado, mas o termo pretende sugerir que o bater das asas da borboleta pode causar o tornado: no sentido de que o bater das asas faz parte das condições iniciais de uma teia complexa interconectada; um conjunto de condições leva a um tornado, enquanto o outro conjunto de condições não. A asa batendo representa uma pequena mudança na condição inicial do sistema, que se propaga para alterações de eventos em larga escala (compare: efeito dominó). Se a borboleta não tivesse batido as asas, a trajetória do sistema poderia ter sido muito diferente – mas também é igualmente possível que o conjunto de condições sem o bater das asas da borboleta seja o conjunto que leva a um tornado.
O efeito borboleta apresenta um desafio óbvio para a previsão, uma vez que as condições iniciais para um sistema como o clima nunca podem ser conhecidas com precisão total. Este problema motivou o desenvolvimento da previsão por conjunto, na qual uma série de previsões são feitas a partir de condições iniciais perturbadas.
Alguns cientistas argumentaram desde então que o sistema meteorológico não é tão sensível às condições iniciais como se acreditava anteriormente. David Orrell argumenta que o principal contribuinte para o erro de previsão do tempo é o erro do modelo, com a sensibilidade às condições iniciais desempenhando um papel relativamente pequeno. Stephen Wolfram também observa que as equações de Lorenz são altamente simplificadas e não contêm termos que representam efeitos viscosos; ele acredita que esses termos tenderiam a amortecer pequenas perturbações. Estudos recentes usando modelos de Lorenz generalizados que incluíram termos dissipativos adicionais e não linearidade sugeriram que um parâmetro de aquecimento maior é necessário para o início do caos.
Enquanto o "efeito borboleta" é frequentemente explicada como sinônimo de dependência sensível de condições iniciais do tipo descrito por Lorenz em seu artigo de 1963 (e observado anteriormente por Poincaré), a metáfora da borboleta foi originalmente aplicada ao trabalho que ele publicou em 1969, que levou a ideia um passo adiante. Lorenz propôs um modelo matemático de como pequenos movimentos na atmosfera aumentam para afetar sistemas maiores. Ele descobriu que os sistemas desse modelo só poderiam ser previstos até um ponto específico no futuro e, além disso, reduzir o erro nas condições iniciais não aumentaria a previsibilidade (desde que o erro não fosse zero). Isso demonstrou que um sistema determinístico poderia ser "observacionalmente indistinguível" de um não determinístico em termos de previsibilidade. Reexames recentes deste artigo sugerem que ele ofereceu um desafio significativo à ideia de que nosso universo é determinístico, comparável aos desafios oferecidos pela física quântica.
No livro intitulado “A Essência do Caos” publicado em 1993, Lorenz definiu o efeito borboleta como: “O fenômeno que uma pequena alteração no estado de um sistema dinâmico causará subseqüentes estados diferem muito dos estados que teriam seguido sem a alteração.” Este recurso é o mesmo que dependência sensível de soluções em condições iniciais (SDIC) em. No mesmo livro, Lorenz aplicou a atividade de esquiar e desenvolveu um modelo de esqui idealizado para revelar a sensibilidade dos caminhos variáveis no tempo para as posições iniciais. Um horizonte de previsibilidade é determinado antes do início do SDIC.
Ilustração
O efeito borboleta no atrator Lorenz tempo 0 ≤)≤ 30 (maior) zangão. coord (maior) 
Estes números mostram dois segmentos da evolução tridimensional de duas trajetórias (uma em azul e outra em amarelo) para o mesmo período do tempo no atrator Lorenz começando em dois pontos iniciais que diferem por apenas 10-5 na coordenada x. Inicialmente, as duas trajetórias parecem coincidentes, como indicado pela pequena diferença entre a zangão. coordenada das trajetórias azul e amarelo, mas para )> 23 a diferença é tão grande quanto o valor da trajetória. A posição final dos cones indica que as duas trajetórias não são mais coincidentes em )- 30. Uma animação do atrator Lorenz mostra a evolução contínua.
Teoria e definição matemática
A recorrência, o retorno aproximado de um sistema às suas condições iniciais, juntamente com a dependência sensível das condições iniciais, são os dois principais ingredientes do movimento caótico. Eles têm a consequência prática de tornar sistemas complexos, como o clima, difíceis de prever além de um determinado intervalo de tempo (aproximadamente uma semana no caso do clima), pois é impossível medir as condições atmosféricas iniciais com total precisão.
Um sistema dinâmico exibe uma dependência sensível das condições iniciais se pontos arbitrariamente próximos se separam ao longo do tempo a uma taxa exponencial. A definição não é topológica, mas essencialmente métrica. Lorenz definiu a dependência sensível da seguinte forma:
A propriedade que caracteriza uma órbita (ou seja, uma solução) se a maioria das outras órbitas que passam perto dela em algum ponto não permanecem próximas dela com o passar do tempo.
Se M é o espaço estatal para o mapa f){displaystyle f^{t}}, então f){displaystyle f^{t}} exibe dependência sensível às condições iniciais se para qualquer x in M e qualquer δ > 0, há y em M, com distância D(..) tal que <math alttext="{displaystyle 0<d(x,y)0<D(x,Sim.)<δ δ {displaystyle 0<d(x,y)<delta ?<img alt="0<d(x,y) e tal que
- mathrm {e} ^{atau },d(x,y)}" xmlns="http://www.w3.org/1998/Math/MathML">D(f? ? (x),f? ? (Sim.))>eum? ? D(x,Sim.){displaystyle d(f^{tau }(x),f^{tau }(y)>mathrm {e} ^{atau },d(x,y)}
mathrm {e} ^{atau },d(x,y)" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/aec11828cac12d3e92c92d43912fd7833d35ebda" style="vertical-align: -0.838ex; width:27.982ex; height:2.843ex;"/>
para algum parâmetro positivo a. A definição não exige que todos os pontos de uma vizinhança se separem do ponto base x, mas requer um expoente de Lyapunov positivo. Além de um expoente de Lyapunov positivo, a limitação é outra característica importante nos sistemas caóticos.
A estrutura matemática mais simples exibindo dependência sensível das condições iniciais é fornecida por uma parametrização particular do mapa logístico:
- xn+1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =4xn(1- Sim. - Sim. xn),0≤ ≤ x0≤ ≤ 1,Não. x_{n+1}=4x_{n}(1-x_{n}),quad 0leq x_{0}leq 1,}
que, ao contrário da maioria dos mapas caóticos, tem uma solução de forma fechada:
- xn= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =pecado2 (2nθ θ D D ){displaystyle x_{n}=sin ^{2}(2^{n}theta pi)}
onde o parâmetro de condição inicial θ θ - Sim. é dado por θ θ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1D D pecado- Sim. - Sim. 1 (x01/2){displaystyle theta ={tfrac Não. }}sin ^{-1}(x_{0}^{1/2})}. Para racional θ θ - Sim., após um número finito de iterações xnNão. x_{n}} mapas em uma sequência periódica. Mas quase tudo θ θ - Sim. são irracionais, e, para irracional θ θ - Sim., xnNão. x_{n}} nunca se repete – não é periódico. Esta equação de solução demonstra claramente as duas principais características do caos – alongamento e dobramento: o fator 2n mostra o crescimento exponencial do alongamento, que resulta na dependência sensível das condições iniciais (o efeito borboleta), enquanto a função de seio quadrado mantém xnNão. x_{n}} dobrado dentro do intervalo [0, 1].
Em sistemas físicos
No clima
O efeito borboleta é mais conhecido em termos de clima; pode ser facilmente demonstrado em modelos de previsão do tempo padrão, por exemplo. Os cientistas climáticos James Annan e William Connolley explicam que o caos é importante no desenvolvimento de métodos de previsão do tempo; os modelos são sensíveis às condições iniciais. Eles acrescentam a ressalva: “É claro que a existência de uma borboleta desconhecida batendo suas asas não tem relação direta com as previsões do tempo, pois levará muito tempo para que uma perturbação tão pequena cresça até um tamanho significativo, e temos muitas incertezas mais imediatas para se preocupar. Portanto, o impacto direto desse fenômeno na previsão do tempo geralmente está um pouco errado." Os dois tipos de efeitos borboleta, incluindo a dependência sensível das condições iniciais e a capacidade de uma pequena perturbação de criar uma circulação organizada em grandes distâncias, não são exatamente os mesmos. Uma comparação entre os dois tipos de efeito borboleta e o terceiro tipo de efeito borboleta foi documentada.
Ao revelar a coexistência de atratores caóticos e não caóticos nos modelos de Lorenz, Shen e seus colegas propuseram uma visão revisada de que “o clima possui caos e ordem”, em contraste com a visão convencional de “o tempo está caótico”. Como resultado, a dependência sensível das condições iniciais (SDIC) nem sempre aparece. Ou seja, SDIC aparece quando duas órbitas (ou seja, soluções) se tornam o atrator caótico; não aparece quando duas órbitas se movem para o mesmo ponto atrator. A animação acima para o movimento do pêndulo duplo fornece uma analogia. Para grandes ângulos de oscilação, o movimento do pêndulo costuma ser caótico. Em comparação, para pequenos ângulos de oscilação, os movimentos não são caóticos.
A multiestabilidade é definida quando um sistema (por exemplo, o sistema de pêndulo duplo) contém mais de um atrator limitado que depende apenas das condições iniciais. A multiestabilidade foi ilustrada usando canoagem na Figura do lado direito (ou seja, Figura 1 de) onde o aparecimento de fortes correntes e uma área estagnada sugere instabilidade e estabilidade local, respectivamente. Como resultado, quando dois caiaques se movem ao longo de fortes correntes, seus caminhos exibem SDIC. Por outro lado, quando dois caiaques se movem para uma área estagnada, eles ficam presos, não apresentando SDIC típico (embora possa ocorrer um transiente caótico). Tais características de SDIC ou não SDIC sugerem dois tipos de soluções e ilustram a natureza da multiestabilidade.
Levando em consideração a multiestabilidade variável no tempo que está associada à modulação de processos de grande escala (por exemplo, forçamento sazonal) e feedback agregado de processos de pequena escala (por exemplo, convecção), a visão revisada acima é refinada da seguinte forma:
"A atmosfera possui caos e ordem; inclui, como exemplos, sistemas organizados emergentes (como tornados) e forçamento variável no tempo de estações recorrentes."
Na mecânica quântica
O potencial de dependência sensível das condições iniciais (o efeito borboleta) foi estudado em vários casos na física semiclássica e quântica, incluindo átomos em campos fortes e o problema anisotrópico de Kepler. Alguns autores argumentaram que a dependência extrema (exponencial) das condições iniciais não é esperada em tratamentos quânticos puros; no entanto, a dependência sensível das condições iniciais demonstrada no movimento clássico está incluída nos tratamentos semiclássicos desenvolvidos por Martin Gutzwiller e John B. Delos e colaboradores. A teoria da matriz aleatória e as simulações com computadores quânticos provam que algumas versões do efeito borboleta na mecânica quântica não existem.
Outros autores sugerem que o efeito borboleta pode ser observado em sistemas quânticos. Zbyszek P. Karkuszewski et al. considere a evolução temporal de sistemas quânticos que possuem hamiltonianos ligeiramente diferentes. Eles investigam o nível de sensibilidade dos sistemas quânticos a pequenas mudanças em seus hamiltonianos. David Poulin e cols. apresentou um algoritmo quântico para medir o decaimento da fidelidade, que "mede a taxa na qual estados iniciais idênticos divergem quando submetidos a dinâmicas ligeiramente diferentes". Eles consideram o decaimento da fidelidade como "o análogo quântico mais próximo do efeito borboleta (puramente clássico)". Enquanto o efeito borboleta clássico considera o efeito de uma pequena mudança na posição e/ou velocidade de um objeto em um determinado sistema hamiltoniano, o efeito borboleta quântico considera o efeito de uma pequena mudança no sistema hamiltoniano com uma dada posição inicial e velocidade. Este efeito borboleta quântica foi demonstrado experimentalmente. Os tratamentos quânticos e semiclássicos da sensibilidade do sistema às condições iniciais são conhecidos como caos quântico.
Na cultura popular
Contenido relacionado
Efeito trado
Núcleo
Telecomunicações no Kuwait