Divergência

ImprimirCitar

Operador vetorial que mede a expansão ou saída de um campo vetorial

A divergência de diferentes campos vetoriais. A divergência de vetores do ponto (x,y) equivale à soma do derivado parcial-com-respeito-a-x do x-componente e do derivado parcial-com-respeito-a-y do y-componente nesse ponto:

{displaystyle nabla !cdot (mathbf {V} (x,y))={frac {partial {V_{x}(x,y)}}{partial {x}}}+{frac {partial {V_{y}(x,y)}}{partial {y}}}}

No cálculo vetorial, divergência é um operador vetorial que opera em um campo vetorial, produzindo um campo escalar que fornece a quantidade da fonte do campo vetorial em cada ponto. Mais tecnicamente, a divergência representa a densidade de volume do fluxo externo de um campo vetorial de um volume infinitesimal em torno de um determinado ponto.

Como exemplo, considere o ar conforme ele é aquecido ou resfriado. A velocidade do ar em cada ponto define um campo vetorial. Enquanto o ar é aquecido em uma região, ele se expande em todas as direções e, portanto, o campo de velocidade aponta para fora dessa região. A divergência do campo de velocidade naquela região teria, portanto, um valor positivo. Enquanto o ar é resfriado e, portanto, contraído, a divergência da velocidade tem um valor negativo.

Interpretação física da divergência

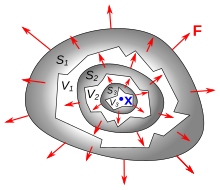
Em termos físicos, a divergência de um campo vetorial é a extensão em que o fluxo do campo vetorial se comporta como uma fonte em um determinado ponto. É uma medida local de sua "saída" – a extensão em que há mais vetores de campo saindo de uma região infinitesimal do espaço do que entrando nela. Um ponto no qual o fluxo está saindo tem divergência positiva e geralmente é chamado de "fonte" do campo. Um ponto no qual o fluxo é direcionado para dentro tem divergência negativa e é frequentemente chamado de "sumidouro" do campo. Quanto maior o fluxo de campo através de uma pequena superfície envolvendo um determinado ponto, maior o valor da divergência naquele ponto. Um ponto no qual há fluxo zero através de uma superfície envolvente tem divergência zero.

A divergência de um campo vetorial é frequentemente ilustrada usando o exemplo simples do campo de velocidade de um fluido, líquido ou gás. Um gás em movimento tem uma velocidade, uma velocidade e uma direção em cada ponto, que pode ser representada por um vetor, de modo que a velocidade do gás forma um campo vetorial. Se um gás for aquecido, ele se expandirá. Isso causará um movimento líquido de partículas de gás para fora em todas as direções. Qualquer superfície fechada no gás envolverá o gás que está se expandindo, então haverá um fluxo de gás para fora através da superfície. Assim, o campo de velocidade terá divergência positiva em todos os lugares. Da mesma forma, se o gás for resfriado, ele se contrairá. Haverá mais espaço para partículas de gás em qualquer volume, então a pressão externa do fluido causará um fluxo líquido de volume de gás para dentro através de qualquer superfície fechada. Portanto, o campo de velocidade tem divergência negativa em todos os lugares. Em contraste, em um gás a temperatura e pressão constantes, o fluxo líquido de gás para fora de qualquer superfície fechada é zero. O gás pode estar se movendo, mas a taxa de volume do gás que flui para dentro de qualquer superfície fechada deve ser igual à taxa de volume que sai, então o fluxo líquido é zero. Assim, a velocidade do gás tem divergência zero em todos os lugares. Um campo que tem divergência zero em todos os lugares é chamado solenoidal.

Se o gás for aquecido apenas em um ponto ou pequena região, ou se for introduzido um pequeno tubo que forneça uma fonte de gás adicional em um ponto, o gás se expandirá, empurrando as partículas de fluido ao seu redor em todas as direções. Isso causará um campo de velocidade externo em todo o gás, centrado no ponto aquecido. Qualquer superfície fechada envolvendo o ponto aquecido terá um fluxo de partículas de gás saindo dela, de modo que haverá divergência positiva nesse ponto. No entanto, qualquer superfície fechada não envolvendo o ponto terá uma densidade constante de gás no interior, portanto, tantas partículas de fluido estão entrando quanto saindo do volume, portanto, o fluxo líquido para fora do volume é zero. Portanto, a divergência em qualquer outro ponto é zero.

Definição

A divergência num ponto

x

é o limite da relação do fluxo

Phi

através da superfície

S Eu...

(setas vermelhas) ao volume

{displaystyle |V_{i}|}

para qualquer sequência de regiões fechadas

V 1, V 2, V 3 ...

Enclosing

x

que aproxima o volume zero:

{displaystyle operatorname {div} mathbf {F} =lim _{|V_{i}|to 0}{frac {Phi (S_{i})}{|V_{i}|}}}

A divergência de um campo vetorial $F (x)$ em um ponto $x 0$ é definido como o limite da razão da integral de superfície de $F$ da superfície fechada de um volume $V$ envolvendo $x 0$ ao volume de $V$ , como $V$ diminui para zero

{displaystyle left.operatorname {div} mathbf {F} right|_{mathbf {x_{0}} }=lim _{Vto 0}{frac {1}{|V|}}}

{displaystyle scriptstyle S(V)}

{displaystyle mathbf {F} cdot mathbf {hat {n}} ,dS}

Onde? $| V |$ é o volume de $V$ , $S (V)$ é o limite de $V$ e $mathbf {hat {n}}$ é a unidade externa normal para essa superfície. Pode-se mostrar que o limite acima sempre converge para o mesmo valor para qualquer sequência de volumes que contenham $x 0$ e aproximar o volume zero. O resultado, $Div F$ , é uma função escalar de $x$ .

Como esta definição é livre de coordenadas, ela mostra que a divergência é a mesma em qualquer sistema de coordenadas. No entanto, não é usado com frequência para calcular a divergência; quando o campo vetorial é fornecido em um sistema de coordenadas, as definições de coordenadas abaixo são muito mais simples de usar.

Um campo vetorial com divergência zero em todos os lugares é chamado de solenoidal – caso em que qualquer superfície fechada não possui fluxo líquido através dela.

Definição em coordenadas

Coordenadas cartesianas

Em coordenadas cartesianas tridimensionais, a divergência de um campo vetorial continuamente diferenciado ${displaystyle mathbf {F} =F_{x}mathbf {i} +F_{y}mathbf {j} +F_{z}mathbf {k} }$ é definido como a função dimensionada:

{displaystyle operatorname {div} mathbf {F} =nabla cdot mathbf {F} =left({frac {partial }{partial x}},{frac {partial }{partial y}},{frac {partial }{partial z}}right)cdot (F_{x},F_{y},F_{z})={frac {partial F_{x}}{partial x}}+{frac {partial F_{y}}{partial y}}+{frac {partial F_{z}}{partial z}}.}

Embora expresso em termos de coordenadas, o resultado é invariante em rotações, como sugere a interpretação física. Isso ocorre porque o traço da matriz jacobiana de um campo vetorial $N$ -dimensional $F$ no espaço $N$ -dimensional é invariante em qualquer transformação linear invertível.

A notação comum para a divergência $\nabla \cdot F$ é um mnemônico conveniente, onde o ponto denota uma operação que lembra o produto escalar: pegue o componentes do operador $\nabla$ (consulte del), aplique-os aos componentes correspondentes de $F$ , e some os resultados. Como aplicar um operador é diferente de multiplicar os componentes, isso é considerado um abuso de notação.

Coordenadas cilíndricas

Para um vetor expresso em coordenadas cilíndricas de unidades locais como

{displaystyle mathbf {F} =mathbf {e} _{r}F_{r}+mathbf {e} _{theta }F_{theta }+mathbf {e} _{z}F_{z},}

onde $e a$ é o vetor unitário na direção $a$ , a divergência é

{displaystyle operatorname {div} mathbf {F} =nabla cdot mathbf {F} ={frac {1}{r}}{frac {partial }{partial r}}left(rF_{r}right)+{frac {1}{r}}{frac {partial F_{theta }}{partial theta }}+{frac {partial F_{z}}{partial z}}.}

O uso de coordenadas locais é vital para a validade da expressão. Se considerarmos $x$ o vetor de posição e as funções $R (x)$ , $θ (x)$ e $zangão. (x)$ , que atribui o correspondente global global coordenada cilíndrica para um vetor, em geral ${displaystyle r(mathbf {F} (mathbf {x}))neq F_{r}(mathbf {x})}$ , ${displaystyle theta (mathbf {F} (mathbf {x}))neq F_{theta }(mathbf {x})}$ e ${displaystyle z(mathbf {F} (mathbf {x}))neq F_{z}(mathbf {x})}$ . Em particular, se considerarmos a função de identidade $F (x) = x$ , nós achamos isso:

{displaystyle theta (mathbf {F} (mathbf {x}))=theta neq F_{theta }(mathbf {x})=0}

Coordenadas esféricas

Em coordenadas esféricas, com $θ$ o ângulo com o $z$ e $φ$ a rotação em torno do estilo z e $F$ novamente escrito em coordenadas de unidade local, a divergência é

{displaystyle operatorname {div} mathbf {F} =nabla cdot mathbf {F} ={frac {1}{r^{2}}}{frac {partial }{partial r}}left(r^{2}F_{r}right)+{frac {1}{rsin theta }}{frac {partial }{partial theta }}(sin theta ,F_{theta })+{frac {1}{rsin theta }}{frac {partial F_{varphi }}{partial varphi }}.}

Campo tensor

Seja $A$ um campo tensor de segunda ordem continuamente diferenciável definido da seguinte forma:

{displaystyle mathbf {A} ={begin{bmatrix}A_{11}&A_{12}&A_{13}\A_{21}&A_{22}&A_{23}\A_{31}&A_{32}&A_{33}end{bmatrix}}}

a divergência no sistema de coordenadas cartesianas é um campo tensor de primeira ordem e pode ser definido de duas maneiras:

{displaystyle operatorname {div} (mathbf {A})={cfrac {partial A_{ik}}{partial x_{k}}}~mathbf {e} _{i}=A_{ik,k}~mathbf {e} _{i}={begin{bmatrix}{dfrac {partial A_{11}}{partial x_{1}}}+{dfrac {partial A_{12}}{partial x_{2}}}+{dfrac {partial A_{13}}{partial x_{3}}}\{dfrac {partial A_{21}}{partial x_{1}}}+{dfrac {partial A_{22}}{partial x_{2}}}+{dfrac {partial A_{23}}{partial x_{3}}}\{dfrac {partial A_{31}}{partial x_{1}}}+{dfrac {partial A_{32}}{partial x_{2}}}+{dfrac {partial A_{33}}{partial x_{3}}}end{bmatrix}}}

{displaystyle nabla cdot mathbf {A} ={cfrac {partial A_{ki}}{partial x_{k}}}~mathbf {e} _{i}=A_{ki,k}~mathbf {e} _{i}={begin{bmatrix}{dfrac {partial A_{11}}{partial x_{1}}}+{dfrac {partial A_{21}}{partial x_{2}}}+{dfrac {partial A_{31}}{partial x_{3}}}\{dfrac {partial A_{12}}{partial x_{1}}}+{dfrac {partial A_{22}}{partial x_{2}}}+{dfrac {partial A_{32}}{partial x_{3}}}\{dfrac {partial A_{13}}{partial x_{1}}}+{dfrac {partial A_{23}}{partial x_{2}}}+{dfrac {partial A_{33}}{partial x_{3}}}\end{bmatrix}}}

Temos

{displaystyle operatorname {div} (mathbf {A^{T}})=nabla cdot mathbf {A} }

Se tensor é simétrico $A ij = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = A ji$ então ${displaystyle operatorname {div} (mathbf {A})=nabla cdot mathbf {A} }$ . Por isso, muitas vezes na literatura as duas definições (e símbolos $Div$ e $nabla cdot$ ) são usados intercambiavelmente (especialmente em equações mecânicas onde a simetria tensor é assumida).

Expressões de ${displaystyle nabla cdot mathbf {A} }$ em coordenadas cilíndricas e esféricas são dadas no artigo del em coordenadas cilíndricas e esféricas.

Coordenadas gerais

Usando a notação de Einstein podemos considerar a divergência em coordenadas gerais, que escrevemos como $x 1, \dots, x i, \dots, x n$ , onde $n$ é o número de dimensões do domínio. Aqui, o índice superior refere-se ao número da coordenada ou componente, então $x 2$ refere-se ao segundo componente, e não a quantidade $x$ ao quadrado. A variável de índice $i$ é usada para se referir a um componente arbitrário, como $x i$ . A divergência pode então ser escrita através da fórmula de Voss-Weyl, como:

{displaystyle operatorname {div} (mathbf {F})={frac {1}{rho }}{frac {partial left(rho ,F^{i}right)}{partial x^{i}}},}

Onde? $rho$ é o coeficiente local do elemento de volume e $F Eu...$ são os componentes de ${displaystyle mathbf {F} =F^{i}mathbf {e} _{i}}$ com respeito ao local não normalizado base covariante (às vezes escrito como ${displaystyle mathbf {e} _{i}=partial mathbf {x} /partial x^{i}}$ ). A notação de Einstein implica a soma sobre $Eu...$ , uma vez que parece um índice superior e inferior.

O coeficiente de volume $?$ é uma função de posição que depende do sistema de coordenadas. Em coordenadas cartesianas, cilíndricas e esféricas, usando as mesmas convenções que antes, temos $? = 1$ , $? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = R$ e $? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = R 2 pecado θ$ , respectivamente. O volume também pode ser expresso como ${textstyle rho ={sqrt {left|det g_{ab}right|}}}$ , onde $g A$ é o tensor métrico. O determinante aparece porque fornece a definição invariante adequada do volume, dada um conjunto de vetores. Uma vez que o determinante é uma quantidade escalar que não depende dos índices, estes podem ser suprimidos, escrevendo ${textstyle rho ={sqrt {left|det gright|}}}$ . O valor absoluto é tomado para lidar com o caso geral onde o determinante pode ser negativo, como em espaços pseudo-Riemannianos. A razão para a raiz quadrada é um pouco sutil: evita efetivamente a contagem dupla como uma vai de coordenadas curvadas para cartesianas, e de volta. O volume (o determinante) também pode ser entendido como o Jacobiano da transformação de Cartesiano para as coordenadas curvilíneas, que para $n = 3$ dá ${textstyle rho =left|{frac {partial (x,y,z)}{partial (x^{1},x^{2},x^{3})}}right|}$ .

Algumas convenções esperam que todos os elementos de base locais sejam normalizados para o comprimento da unidade, como foi feito nas seções anteriores. Se escrevermos ${hat {mathbf {e} }}_{i}$ para a base normalizada, e ${displaystyle {hat {F}}^{i}}$ para os componentes de $F$ com respeito a isso, temos isso

{displaystyle mathbf {F} =F^{i}mathbf {e} _{i}=F^{i}|{mathbf {e} _{i}}|{frac {mathbf {e} _{i}}{|mathbf {e} _{i}|}}=F^{i}{sqrt {g_{ii}}},{hat {mathbf {e} }}_{i}={hat {F}}^{i}{hat {mathbf {e} }}_{i},}

usando uma das propriedades do tensor métrico. Dotando ambos os lados da última igualdade com o elemento contravariante ${displaystyle {hat {mathbf {e} }}^{i}}$ , podemos concluir que ${textstyle F^{i}={hat {F}}^{i}/{sqrt {g_{ii}}}}$ . Depois de substituir, a fórmula torna-se:

{displaystyle operatorname {div} (mathbf {F})={frac {1}{rho }}{frac {partial left({frac {rho }{sqrt {g_{ii}}}}{hat {F}}^{i}right)}{partial x^{i}}}={frac {1}{sqrt {det g}}}{frac {partial left({sqrt {frac {det g}{g_{ii}}}},{hat {F}}^{i}right)}{partial x^{i}}}.}

Consulte § Em coordenadas curvilíneas para uma discussão mais aprofundada.

Propriedades

As seguintes propriedades podem ser todas derivadas das regras de diferenciação comuns do cálculo. Mais importante ainda, a divergência é um operador linear, ou seja,

{displaystyle operatorname {div} (amathbf {F} +bmathbf {G})=aoperatorname {div} mathbf {F} +boperatorname {div} mathbf {G} }

para todos os campos vetoriais $F$ e $G$ e todos números reais $a$ e $b$ .

Existe uma regra de produto do seguinte tipo: se $φ$ for uma função de valor escalar e $F$ é um campo vetorial, então

{displaystyle operatorname {div} (varphi mathbf {F})=operatorname {grad} varphi cdot mathbf {F} +varphi operatorname {div} mathbf {F}}

ou em notação mais sugestiva

{displaystyle nabla cdot (varphi mathbf {F})=(nabla varphi)cdot mathbf {F} +varphi (nabla cdot mathbf {F}).}

Outra regra de produto para o produto cruzado de dois campos vetoriais $F$ e $G$ em três dimensões envolve o curl e tem a seguinte redação:

{displaystyle operatorname {div} (mathbf {F} times mathbf {G})=operatorname {curl} mathbf {F} cdot mathbf {G} -mathbf {F} cdot operatorname {curl} mathbf {G}}

{displaystyle nabla cdot (mathbf {F} times mathbf {G})=(nabla times mathbf {F})cdot mathbf {G} -mathbf {F} cdot (nabla times mathbf {G}).}

O laplaciano de um campo escalar é a divergência do gradiente do campo:

{displaystyle operatorname {div} (operatorname {grad} varphi)=Delta varphi.}

A divergência do rotacional de qualquer campo vetorial (em três dimensões) é igual a zero:

{displaystyle nabla cdot (nabla times mathbf {F})=0.}

Se um campo vetorial $F$ com divergência zero é definido em uma bola em $R 3$ , então existe algum campo vetorial $G$ na bola com $F = curl G$ . Para regiões em $R 3$ mais complicadas topologicamente do que essa, a última afirmação pode ser falsa (consulte o lema de Poincaré). O grau de falha da veracidade da afirmação, medido pela homologia do complexo da cadeia

{displaystyle {{text{scalar fields on }}U}~{overset {operatorname {grad} }{rightarrow }}~{{text{vector fields on }}U}~{overset {operatorname {curl} }{rightarrow }}~{{text{vector fields on }}U}~{overset {operatorname {div} }{rightarrow }}~{{text{scalar fields on }}U}}

serve como uma boa quantificação da complexidade da região subjacente $U$ . Estes são os primórdios e principais motivações da cohomologia de Rham.

Teorema da decomposição

Pode ser mostrado que qualquer fluxo estacionário $v (r)$ que é duas vezes continuamente diferenciável em $R 3$ e desaparece rápido o suficiente para $| r | \to \infty$ pode ser decomposto exclusivamente em uma parte irrotacional $E (r)$ e uma parte sem fonte $B (r)$ . Além disso, essas partes são explicitamente determinadas pelas respectivas densidades de origem (veja acima) e densidades de circulação (veja o artigo Curl):

Para a parte irrotacional tem-se

{displaystyle mathbf {E} =-nabla Phi (mathbf {r}),}

com

{displaystyle Phi (mathbf {r})=int _{mathbb {R} ^{3}},d^{3}mathbf {r} ';{frac {operatorname {div} mathbf {v} (mathbf {r} ')}{4pi left|mathbf {r} -mathbf {r} 'right|}}.}

A parte sem fonte, $B$ , pode ser escrita de forma semelhante: basta substituir o potencial escalar $Φ(r)$ por um potencial vetorial $A (r)$ e os termos $-\nablaΦ$ por $+\nabla \times A$ e a densidade da fonte $div v$ pela densidade de circulação $\nabla \times v$ .

Este "teorema da decomposição" é um subproduto do caso estacionário da eletrodinâmica. É um caso especial da decomposição mais geral de Helmholtz, que também funciona em dimensões maiores que três.

Em dimensões finitas arbitrárias

A divergência de um campo vetorial pode ser definida em qualquer número finito $n$ de dimensões. Se

{displaystyle mathbf {F} =(F_{1},F_{2},ldots F_{n}),}

em um sistema de coordenadas euclidianas com coordenadas $x 1, x 2,..., x n$ , defina

{displaystyle operatorname {div} mathbf {F} =nabla cdot mathbf {F} ={frac {partial F_{1}}{partial x_{1}}}+{frac {partial F_{2}}{partial x_{2}}}+cdots +{frac {partial F_{n}}{partial x_{n}}}.}

No caso 1D, $F$ se reduz a uma função regular e a divergência se reduz à derivada.

Para qualquer $n$ , a divergência é um operador linear e satisfaz a "regra do produto"

{displaystyle nabla cdot (varphi mathbf {F})=(nabla varphi)cdot mathbf {F} +varphi (nabla cdot mathbf {F})}

para qualquer função com valor escalar $φ$ .

Relação com a derivada externa

Pode-se expressar a divergência como um caso particular da derivada externa, que leva uma forma 2 para uma forma 3 em $R 3$ . Defina a forma dupla atual como

{displaystyle j=F_{1},dywedge dz+F_{2},dzwedge dx+F_{3},dxwedge dy.}

Ele mede a quantidade de "coisas" fluindo através de uma superfície por unidade de tempo em um "fluido de enchimento" de densidade $ρ = 1 dx \land dy \land dz$ movendo-se com velocidade local $F$ . Sua derivada externa $dj$ é então dada por

{displaystyle dj=left({frac {partial F_{1}}{partial x}}+{frac {partial F_{2}}{partial y}}+{frac {partial F_{3}}{partial z}}right)dxwedge dywedge dz=(nabla cdot {mathbf {F} })rho }

Onde? $wedge$ é o produto de cunha.

Assim, a divergência do campo vetorial $F$ pode ser expressa como:

{displaystyle nabla cdot {mathbf {F} }={star }d{star }{big (}{mathbf {F} }^{flat }{big)}.}

Aqui o superscrito ? é um dos dois isomorfismos musicais, e $Detalhe$ é o operador estrela Hodge. Quando a divergência é escrita desta forma, o operador ${displaystyle {star }d{star }}$ é referido como o codiferente. Trabalhar com a corrente de duas formas e o derivado exterior é geralmente mais fácil do que trabalhar com o campo vetorial e divergência, porque ao contrário da divergência, o derivado exterior comuta com uma mudança do sistema de coordenadas (curvilinear).

Em coordenadas curvilíneas

A expressão apropriada é mais complicada em coordenadas curvilíneas. A divergência de um campo vetorial se estende naturalmente a qualquer variedade diferenciável de dimensão $n$ que tenha uma forma de volume (ou densidade) $μ$ , ex. uma variedade Riemanniana ou Lorentziana. Generalizando a construção de uma forma dupla para um campo vetorial em $R 3$ , em tal variedade um campo vetorial $X$ define uma forma $(n - 1)$ $j = i X μ$ obtido contraindo $X$ com $μ$ . A divergência é então a função definida por

{displaystyle dj=(operatorname {div} X)mu.}

A divergência pode ser definida em termos da derivada de Lie como

{displaystyle {mathcal {L}}_{X}mu =(operatorname {div} X)mu.}

Isso significa que a divergência mede a taxa de expansão de uma unidade de volume (um elemento de volume) à medida que flui com o campo vetorial.

Em uma variedade pseudo-Riemanniana, a divergência em relação ao volume pode ser expressa em termos da conexão Levi-Civita $\nabla$ :

{displaystyle operatorname {div} X=nabla cdot X={X^{a}}_{;a},}

onde a segunda expressão é a contração do campo vetorial com valor 1 de forma $\nabla X$ consigo mesmo e a última expressão é a expressão coordenada tradicional do cálculo de Ricci.

Uma expressão equivalente sem usar uma conexão é

{displaystyle operatorname {div} (X)={frac {1}{sqrt {left|det gright|}}},partial _{a}left({sqrt {left|det gright|}},X^{a}right),}

Onde? $g$ é a métrica e $partial _{a}$ denota o derivado parcial em relação à coordenada $x um$ . A raiz quadrada da métrica (valor absoluto do determinante) aparece porque a divergência deve ser escrita com a concepção correta do volume. Nas coordenadas curvilineares, os vetores de base não são mais ortonormais; o determinante codifica a ideia correta do volume neste caso. Parece duas vezes, aqui, uma vez, para que o ${displaystyle X^{a}}$ pode ser transformado em "espaço flash" (onde as coordenadas são realmente ortonormais), e mais uma vez para que $partial _{a}$ é também transformado em "espaço flutuante", de modo que, finalmente, a divergência "ordinária" pode ser escrita com o conceito "ordinário" de volume no espaço plano (Ou seja. volume da unidade, Ou seja. Um. Ou seja. não escrito). A raiz quadrada aparece no denominador, porque o derivado transforma-se no caminho oposto (contravariantemente) ao vetor (que é covariante). Esta ideia de chegar a um "sistema de coordenadas planas" onde as computações locais podem ser feitas de forma convencional é chamado de vielbein. Uma maneira diferente de ver isso é observar que a divergência é a codiferencialidade disfarçada. Ou seja, a divergência corresponde à expressão ${displaystyle star dstar }$ com $d$ o diferencial e $star$ a estrela Hodge. A estrela Hodge, por sua construção, faz com que a forma de volume apareça em todos os lugares certos.

A divergência de tensores

A divergência também pode ser generalizada para tensores. Na notação de Einstein, a divergência de um vetor contravariante $F μ$ é dado por

{displaystyle nabla cdot mathbf {F} =nabla _{mu }F^{mu },}

onde $\nabla μ$ denota a derivada covariante. Nesse cenário geral, a formulação correta da divergência é reconhecer que ela é um codiferencial; as propriedades apropriadas seguem a partir daí.

De forma equivalente, alguns autores definem a divergência de um tensor misto usando o isomorfismo musical ♯: se $T$ é um $(p, q)$ -tensor ( $p$ para o vetor contravariante e $q$ para a covariante), então definimos a divergência de $T$ para ser o $(p, q - 1)$ -tensor

{displaystyle (operatorname {div} T)(Y_{1},ldotsY_{q-1})={operatorname {trace} }{Big (}Xmapsto sharp (nabla T)(X,cdotY_{1},ldotsY_{q-1}){Big)};}

Isto é, nós pegamos o rasto sobre o Primeiro dois. índices covariantes do derivado covariante. O $sharp$ símbolo refere-se ao isomorfismo musical.

Contenido relacionado

Más resultados...