Distribuição normal
Em estatística, uma distribuição normal ou distribuição Gaussiana é um tipo de distribuição de probabilidade contínua para uma variável aleatória de valor real. A forma geral de sua função de densidade de probabilidade é
- f(x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1σ σ 2D D e- Sim. - Sim. 12(x- Sim. - Sim. μ μ σ σ )2{displaystyle f(x)={frac {1}{sigma {2pi }}e^{-{frac {1}{2}}left({frac {x-mu }{sigma }}right)^{2}}}
O parâmetro μ μ - Sim. é a média ou expectativa da distribuição (e também sua mediana e modo), enquanto o parâmetro σ σ - Sim. é seu desvio padrão. A variância da distribuição é σ σ 2{displaystyle sigma ^{2}}. Diz-se que uma variável aleatória com distribuição gaussiana normalmente distribuídoe é chamado de desvio normal.
As distribuições normais são importantes em estatística e são freqüentemente usadas nas ciências naturais e sociais para representar variáveis aleatórias de valor real cujas distribuições não são conhecidas. Sua importância se deve em parte ao teorema do limite central. Ele afirma que, sob algumas condições, a média de muitas amostras (observações) de uma variável aleatória com média e variância finitas é ela própria uma variável aleatória - cuja distribuição converge para uma distribuição normal à medida que o número de amostras aumenta. Portanto, as quantidades físicas que se espera serem a soma de muitos processos independentes, como erros de medição, geralmente têm distribuições quase normais.
Além disso, as distribuições gaussianas têm algumas propriedades únicas que são valiosas em estudos analíticos. Por exemplo, qualquer combinação linear de uma coleção fixa de desvios normais é um desvio normal. Muitos resultados e métodos, como propagação de incerteza e ajuste de parâmetros de mínimos quadrados, podem ser derivados analiticamente de forma explícita quando as variáveis relevantes são normalmente distribuídas.
Às vezes, uma distribuição normal é informalmente chamada de curva de sino. No entanto, muitas outras distribuições são em forma de sino (como Cauchy, t de Student e distribuições logísticas). Para outros nomes, consulte Nomenclatura.
A distribuição de probabilidade univariada é generalizada para vetores na distribuição normal multivariada e para matrizes na distribuição normal de matriz.
Definições
Distribuição normal padrão
O caso mais simples de uma distribuição normal é conhecido como o distribuição normal padrão ou distribuição normal da unidade. Este é um caso especial quando μ μ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle mu =0} e σ σ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1{displaystyle sigma} - Sim., e é descrito por esta função de densidade de probabilidade (ou densidade):
- φ φ (zangão.)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =e- Sim. - Sim. zangão.2/22D D {displaystyle varphi (z)={frac {e^{-z^{2}/2}}{sqrt {2pi }}}}
A variável zangão.Não. tem uma média de 0 e uma variância e desvio padrão de 1. A densidade φ φ (zangão.){displaystyle varphi (z)} tem seu pico 1/2D D {displaystyle 1/{sqrt {2pi }}} em zangão.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0- Sim. e pontos de inflexão zangão.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =+1- Sim. e zangão.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 1Não. - Sim..
Embora a densidade acima seja mais comumente conhecida como normal padrão, alguns autores usaram esse termo para descrever outras versões da distribuição normal. Carl Friedrich Gauss, por exemplo, uma vez definiu a normal padrão como
- φ φ (zangão.)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =e- Sim. - Sim. zangão.2D D {displaystyle varphi (z)={frac {e^{-z^{2}}}{sqrt {pi Sim.
que tem uma variação de 1/2, e Stephen Stigler uma vez definiu o padrão normal como
- φ φ (zangão.)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =e- Sim. - Sim. D D zangão.2{displaystyle varphi (z)=e^{-pi z^{2}}}
que tem uma forma funcional simples e uma variância σ σ 2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1/(2D D ){displaystyle sigma ^{2}=1/(2pi)}
Distribuição normal geral
Cada distribuição normal é uma versão da distribuição normal padrão, cujo domínio foi esticado por um fator σ σ - Sim. (o desvio padrão) e depois traduzido por μ μ - Sim. (o valor médio):
- f(x∣ ∣ μ μ ,σ σ 2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1σ σ φ φ (x- Sim. - Sim. μ μ σ σ ){displaystyle f(xmid musigma ^{2})={frac {1}{sigma }}varphi left({frac {x-mu }{sigma }}right)}
A densidade de probabilidade deve ser dimensionada 1/σ σ - Não. para que a integral ainda seja 1.
Se Z.Não. é um desvio normal padrão, então X= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =σ σ Z.+μ μ Não. X=sigma Z+mu } terá uma distribuição normal com o valor esperado μ μ - Sim. e desvio padrão σ σ - Sim.. Isto equivale a dizer que a distribuição normal "padrão" Z.Não. pode ser dimensionado/forçado por um fator de σ σ - Sim. e deslocado por μ μ - Sim. para produzir uma distribuição normal diferente, chamada X- Sim.. Por outro lado, se X- Sim. é um desvio normal com parâmetros μ μ - Sim. e σ σ 2{displaystyle sigma ^{2}}Então isto X- Sim. a distribuição pode ser redimensionada e deslocada através da fórmula Z.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(X- Sim. - Sim. μ μ )/σ σ {displaystyle Z=(X-mu)/sigma } converter para a distribuição normal "padrão". Este varite também é chamado de forma padronizada de X- Sim..
Notação
A densidade de probabilidade da distribuição Gaussiana padrão (distribuição normal padrão, com variância média zero e unidade) é frequentemente denotada com a letra grega φ φ - Sim. (phi). A forma alternativa da letra grega phi, φ φ - Sim., também é usado bastante frequentemente.
A distribuição normal é frequentemente referida como N(μ μ ,σ σ 2){displaystyle N(musigma ^{2})} ou N(μ μ ,σ σ 2){displaystyle {mathcal {N}}(musigma ^{2})}. Assim, quando uma variável aleatória X- Sim. é normalmente distribuído com média μ μ - Sim. e desvio padrão σ σ - Sim., um pode escrever
- X∼ ∼ N(μ μ ,σ σ 2).Não. Xsim {mathcal {N}}(musigma ^{2}). ?
Parametrizações alternativas
Alguns autores defendem a precisão ? ? - Sim. como o parâmetro que define a largura da distribuição, em vez do desvio σ σ - Sim. ou a variância σ σ 2{displaystyle sigma ^{2}}. A precisão é normalmente definida como o recíproco da variância, 1/σ σ 2{displaystyle 1/sigma ^{2}}. A fórmula para a distribuição torna-se então
- f(x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? 2D D e- Sim. - Sim. ? ? (x- Sim. - Sim. μ μ )2/2.(x)={sqrt {frac {tau }{2pi }}}e^{-tau (x-mu)^{2}/2}.}
Esta escolha é reivindicada ter vantagens em computação numérica quando σ σ - Sim. é muito próximo de zero, e simplifica fórmulas em alguns contextos, como na inferência bayesiana de variáveis com distribuição normal multivariada.
Alternativamente, o reciprocal do desvio padrão ? ? ? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1/σ σ (em inglês) ? pode ser definido como precisão, em que caso a expressão da distribuição normal se torna
- f(x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? ? ? 2D D e- Sim. - Sim. (? ? ? ? )2(x- Sim. - Sim. μ μ )2/2.{displaystyle f(x)={frac {tau ^{prime }}{sqrt {2pi }}}e^{-(tau ^{prime })^{2}(x-mu)^{2}/2}.}
De acordo com Stigler, esta formulação é vantajosa por causa de uma fórmula muito mais simples e fácil de lembrar, e fórmulas aproximadas simples para os quantis da distribuição.
As distribuições normais formam uma família exponencial com parâmetros naturais θ θ 1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ σ σ 2{displaystyle textstyle theta _{1}={frac {mu }{sigma ^{2}}}} e θ θ 2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 12σ σ 2{displaystyle textstyle theta _{2}={frac {-1}{2sigma ^{2}}}}, e estatísticas naturais x e x2. Os parâmetros de dupla expectativa para distribuição normal são ?1 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = μ e ?2 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = μ2 + σ2.
Funções de distribuição cumulativas
A função de distribuição cumulativa (CDF) da distribuição normal padrão, geralmente denotada com a letra grega capital Φ Φ Não. Não. (phi), é a integral
- Φ Φ (x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12D D ∫ ∫ - Sim. - Sim. ∞ ∞ xe- Sim. - Sim. )2/2D){displaystyle Phi (x)={frac {1}{sqrt {2pi }}}int _{-infty }^{x}e^{-t^{2}/2},dt}
A função de erro relacionada E (x)(x)} dá a probabilidade de uma variável aleatória, com distribuição normal de média 0 e variância 1/2 caindo no intervalo Não.- Sim. - Sim. x,x][displaystyle [-x,x]}. Isso é:
- E (x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2D D ∫ ∫ 0xe- Sim. - Sim. )2D){displaystyle operatorname {erf} (x)={frac {2}{sqrt {pi }}}int _{0}^{x}e^{-t^{2}},dt}
Essas integrais não podem ser expressas em termos de funções elementares, e muitas vezes são chamadas de funções especiais. No entanto, muitas aproximações numéricas são conhecidas; veja abaixo para mais.
As duas funções estão intimamente relacionadas, ou seja,
- Φ Φ (x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12Não.1+E (x2)]Não. Phi (x)={frac {1}{2}}left[1+operatorname {erf} left({frac {x}{sqrt {2}}}right)right]}
Para uma distribuição normal genérica com densidade fNão.Quero dizer... μ μ - Sim. e desvio σ σ - Sim., a função de distribuição cumulativa é
- F(x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Φ Φ (x- Sim. - Sim. μ μ σ σ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12Não.1+E (x- Sim. - Sim. μ μ σ σ 2)]{displaystyle F(x)=Phi left({frac {x-mu) }{sigma }}right)={frac {1}{2}}left[1+operatorname {erf} left({frac {x-mu }{sigma {sqrt {2}}}}right]}
O complemento do CDF normal padrão, Q(x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1- Sim. - Sim. Φ Φ (x)(x)=1-Phi (x)}, é frequentemente chamado de Q-função, especialmente em textos de engenharia. Dá a probabilidade de que o valor de uma variável aleatória normal padrão X- Sim. exceda xNão.: x)}" xmlns="http://www.w3.org/1998/Math/MathML">P(X>x)(X>x)}x)}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/767fd276524cfb3556093722a4f40a9209194ea5" style="vertical-align: -0.838ex; width:9.963ex; height:2.843ex;"/>. Outras definições das QNão.-função, todas elas são transformações simples de Φ Φ Não. Não., também são usados ocasionalmente.
O gráfico do CDF normal padrão Φ Φ Não. Não. tem 2 vezes simetria rotacional em torno do ponto (0,1/2); isto é, Φ Φ (- Sim. - Sim. x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1- Sim. - Sim. Φ Φ (x)Não. Phi (-x)=1-Phi (x)}. Seu antiderivativo (indefinido integral) pode ser expresso da seguinte forma:
- ∫ ∫ Φ Φ (x)Dx= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =xΦ Φ (x)+φ φ (x)+C.{displaystyle int Phi (x),dx=xPhi (x)+varphi (x)+C.}
O CDF da distribuição normal padrão pode ser expandido por Integração por partes em uma série:
- Φ Φ (x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12+12D D )) e- Sim. - Sim. x2/2Não.x+x33+x53)) 5+⋯ ⋯ +x2n+1(2n+1)!!+⋯ ⋯ ]Não. Phi (x)={frac {1}{2}}+{frac {1}{sqrt {2pi }}}cdot e^{-x^{2}/2}left[x+{frac {x^{3}}{3}}+{frac {x^{5}}{3cdot 5}}+cdots +{frac {x^{2n+1}}{(2n+1)!}}+cdots right]}
Onde? !!! denota o factorial duplo.
Uma expansão assintótica do CDF para x grande também pode ser derivada usando a integração por partes. Para saber mais, consulte Função de erro#Expansão assintótica.
Uma aproximação rápida para o CDF da distribuição normal padrão pode ser encontrada usando uma aproximação da série de Taylor:
Φ Φ (x)? ? 12+12D D Gerenciamento Gerenciamento k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0n(- Sim. - Sim. 1)kx(2k+1)2kk!(2k+1)Não. Phi (x)approx {frac {1}{2}+{frac {1}{sqrt {2pi }}}sum _{k=0}^{n}{frac {left(-1right)^{k}x^{left(2k+1right)}}{2^{k}k!left(2k+1right)}}}
Cálculo recursivo com expansão Taylor Series
A natureza recursiva da eumx2{displaystyle e^{ax^{2}}}família de derivados pode ser usado para construir facilmente uma expansão da série Taylor rapidamente convergente usando entradas recursivas sobre qualquer ponto do valor conhecido da distribuição,Φ Φ (x0)(x_{0})}:
Φ Φ (x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0∞ ∞ Φ Φ (n)(x0)n!(x- Sim. - Sim. x0)nNão. Phi (x)=sum _{n=0}^{infty }{frac {Phi ^{(n)}(x_{0})}{n!}}(x-x_{0})^{n}}
Onde:
Φ Φ (0)(x0)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12D D ∫ ∫ - Sim. - Sim. ∞ ∞ x0e- Sim. - Sim. )2/2D)(x_{0})={frac {1}{sqrt {2pi }}}int _{-infty }^{x_{0}}e^{-t^{2}/2},dt}
Φ Φ (1)(x0)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12D D e- Sim. - Sim. x02/2{displaystyle Phi ^{(1)}(x_{0})={frac {1}{sqrt {2pi }}}e^{-x_{0}^{2}/2}}
Φ Φ (n)(x0)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. (x0Φ Φ (n- Sim. - Sim. 1)(x0)+(n- Sim. - Sim. 2)Φ Φ (n- Sim. - Sim. 2)(x0)){displaystyle Phi ^{(n)}(x_{0})=-(x_{0}Phi ^{(n-1)}(x_{0})+(n-2)Phi ^{(n-2)}(x_{0})})}, para todos n ≥ 2.
Usando a série de Taylor e o método de Newton para a função inversa
Uma aplicação para a expansão da série Taylor acima é usar o método de Newton para reverter a computação. Ou seja, se tivermos um valor para o CDF, Φ Φ (x)(x)}, mas não sabe o x necessário para obter o Φ Φ (x)(x)}, podemos usar o método de Newton para encontrar x, e usar a expansão da série Taylor acima para minimizar o número de cálculos. O método de Newton é ideal para resolver este problema porque o primeiro derivado de Φ Φ (x)(x)}, que é uma parte integrante da distribuição normal padrão, é a distribuição padrão normal, e está prontamente disponível para usar na solução de método de Newton.
Para resolver, selecione uma solução aproximada conhecida, x0{displaystyle x_{0}}, ao desejado Φ Φ (x)(x)}. x0{displaystyle x_{0}} pode ser um valor de uma tabela de distribuição, ou uma estimativa inteligente seguida por uma computação Φ Φ (x0)(x_{0})} usando qualquer meio desejado para calcular. Use este valor de x0{displaystyle x_{0}} e a expansão da série Taylor acima para minimizar as computações.
Repita o seguinte processo até a diferença entre o computadorizado Φ Φ (xn)(x_{n})} e o desejado Φ Φ Não. Não.O que vamos chamar Φ Φ (DeSEu...ReD)Não. Phi (mathrm {Desired})}, está abaixo de um erro aceitável pequeno escolhido, como 1.e-05, 1.e-15, etc:
Onde
Φ Φ (x,x0,Φ Φ (x0))Não. Phi (x,x_{0},Phi (x_{0})})} é o Φ Φ (x)(x)} de uma solução de série Taylor usando x0{displaystyle x_{0}} e Φ Φ (x0)(x_{0})}
Φ Φ ?(x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12D D e- Sim. - Sim. x2/2Não. Phi '(x)={frac {1}{sqrt {2pi }}}e^{-x^{2}/2}}
Quando as computações repetidas convergem para um erro abaixo do valor aceitavelmente pequeno escolhido, x será o valor necessário para obter um Φ Φ (x)(x)} do valor desejado, Φ Φ (DeSEu...ReD)Não. Phi (mathrm {Desired})}. Se x0{displaystyle x_{0}} é uma boa estimativa inicial, a convergência deve ser rápida com apenas um pequeno número de iterações necessárias.
Desvio padrão e cobertura
Cerca de 68% dos valores extraídos de uma distribuição normal estão dentro de um desvio padrão σ da média; cerca de 95% dos valores estão dentro de dois desvios padrão; e cerca de 99,7% estão dentro de três desvios padrão. Esse fato é conhecido como regra 68-95-99,7 (empírica) ou regra dos 3 sigmas.
Mais precisamente, a probabilidade de um desvio normal estar no intervalo entre μ μ - Sim. - Sim. nσ σ - Sim. e μ μ +nσ σ {displaystyle mu +nsigma } é dado por
- F(μ μ +nσ σ )- Sim. - Sim. F(μ μ - Sim. - Sim. nσ σ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Φ Φ (n)- Sim. - Sim. Φ Φ (- Sim. - Sim. n)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =E (n2).{displaystyle F(mu +nsigma)-F(mu -nsigma)=Phi (n)-Phi (-n)=operatorname {erf} left({frac {n}{sqrt {2}}}right). ?
Para 12 dígitos significativos, os valores para n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1,2,...... ,6- Não. são:
| nNão. | p= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =F(μ μ +nσ σ )- Sim. - Sim. F(μ μ - Sim. - Sim. nσ σ ){displaystyle p=F(mu +nsigma)-F(mu -nsigma)} | Ou seja.1- Sim. - Sim. pNão. }}1-p | ou1emp{displaystyle {text{or }}1{text{in }}p} | OEIS | ||
|---|---|---|---|---|---|---|
| 1 | 0,682689492137 | 0.317310507863 |
| OEIS: A178647 | ||
| 2 | 0,954499736104 | 0,045500.263896 |
| OEIS: A110894 | ||
| 3 | 0.997300203937 | 0,002699796063 |
| OEIS: A270712 | ||
| 4 | 0,999936657516 | 0,000063342484 |
| |||
| 5 | 0,999999426697 | 0,000)573303 |
| |||
| 6 | 0,999999998027 | 0,000)001973 |
|
Para grande nNão., pode-se usar a aproximação 1- Sim. - Sim. p? ? e- Sim. - Sim. n2/2nD D /2{displaystyle 1-papprox {frac {e^{-n^{2}/2}}{n{sqrt Sim..
Função quantílica
A função quantil de uma distribuição é o inverso da função de distribuição cumulativa. A função quantil da distribuição normal padrão é chamada de função probit e pode ser expressa em termos da função de erro inversa:
- Φ Φ - Sim. - Sim. 1(p)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2E- Sim. - Sim. 1 (2p- Sim. - Sim. 1),p∈ ∈ (0,1).Não. Phi ^{-1}(p)={sqrt {2}}operatorname {erf} ^{-1}(2p-1),quad pin (0,1). ?
Para uma variável aleatória normal com média μ μ - Sim. e variância σ σ 2{displaystyle sigma ^{2}}, a função quantil é
- F- Sim. - Sim. 1(p)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ +σ σ Φ Φ - Sim. - Sim. 1(p)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ +σ σ 2E- Sim. - Sim. 1 (2p- Sim. - Sim. 1),p∈ ∈ (0,1).{displaystyle F^{-1}(p)=mu +sigma Phi ^{-1}(p)=mu +sigma {sqrt {2}}operatorname {erf} ^{-1}(2p-1),quad pin (0,1). ?
O quantil Φ Φ - Sim. - Sim. 1(p)Não. Phi ^{-1}(p)} da distribuição normal padrão é comumente denotada como zangão.pNão. Z_{p}}. Esses valores são usados em testes de hipóteses, construção de intervalos de confiança e gráficos Q-Q. Uma variável aleatória normal X- Sim. exceda μ μ +zangão.pσ σ {displaystyle mu +z_{p}sigma } com probabilidade 1- Sim. - Sim. pNão., e vai ficar fora do intervalo μ μ ± ± zangão.pσ σ {displaystyle mu pm z_{p}sigma } com probabilidade 2(1- Sim. - Sim. p){displaystyle 2(1-p)}. Em particular, o quantil zangão.0.975{displaystyle z_{0.975}} é 1,96; portanto, uma variável aleatória normal estará fora do intervalo μ μ ± ± 1.96σ σ {displaystyle mu pm 1.96sigma } em apenas 5% dos casos.
A tabela a seguir dá o quantil zangão.pNão. Z_{p}} tal que X- Sim. vai mentir no intervalo μ μ ± ± zangão.pσ σ {displaystyle mu pm z_{p}sigma } com uma probabilidade especificada pNão.. Esses valores são úteis para determinar o intervalo de tolerância para médias de amostra e outros estimadores estatísticos com distribuições normais (ou assintoticamente normais). Note que a tabela a seguir mostra 2E- Sim. - Sim. 1 (p)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Φ Φ - Sim. - Sim. 1(p+12){displaystyle {sqrt {2}}operatorname {erf} ^{-1}(p)=Phi ^{-1}left({frac {p+1}{2}}right)}, não Φ Φ - Sim. - Sim. 1(p)Não. Phi ^{-1}(p)} como definido acima.
| pNão. | zangão.pNão. Z_{p}} | pNão. | zangão.pNão. Z_{p}} | |
|---|---|---|---|---|
| 0,80 | 1.281551565545 | 0,999 | 3.290526731492 | |
| 0,90 | 1.644853626951 | 0,9999 | 3.890591886413 | |
| 0,95 | 1.959963984540 | 0,99999 | 4.417173413469 | |
| 0,98 | 2.326347874041 | 999.99.99.99.99.99.99.99.99.99.99.99.99.99.99.99.99.99.99.99.99.99.99.99.99.99.99.99.99.99.99. | 4.891638475699 | |
| 0,99 | 2.575829303549 | 9.999 | 5.326723886384 | |
| 0,995 | 2.807033768344 | 999.99 | 5.730728868236 | |
| 0,998 | 3.090232306168 | 9.99999 | 6.109410204869 |
Para pequeno pNão., a função quantil tem a expansão assintotic útil Φ Φ - Sim. - Sim. 1(p)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. I 1p2- Sim. - Sim. I I 1p2- Sim. - Sim. I (2D D )+o(1).Não. Phi ^{-1}(p)=-{sqrt {ln {frac {1}{p^{2}}}-ln ln {1}{p^{2}}}-ln(2pi)}}+{mathcal {o}}(1).}
Propriedades
A distribuição normal é a única distribuição cujos cumulantes além dos dois primeiros (isto é, exceto a média e a variância) são zero. É também a distribuição contínua com a entropia máxima para uma média e variância especificadas. Geary mostrou, assumindo que a média e a variância são finitas, que a distribuição normal é a única distribuição em que a média e a variância calculadas a partir de um conjunto de extrações independentes são independentes uma da outra.
A distribuição normal é uma subclasse das distribuições elípticas. A distribuição normal é simétrica em relação à sua média e é diferente de zero em toda a linha real. Como tal, pode não ser um modelo adequado para variáveis inerentemente positivas ou fortemente distorcidas, como o peso de uma pessoa ou o preço de uma ação. Tais variáveis podem ser melhor descritas por outras distribuições, como a distribuição log-normal ou a distribuição de Pareto.
O valor da distribuição normal é praticamente zero quando o valor xNão. Encontra-se mais do que alguns desvios padrão fora da média (por exemplo, uma propagação de três desvios padrão abrange todos, mas 0,27% da distribuição total). Portanto, pode não ser um modelo apropriado quando se espera uma fração significativa de outliers - valores que estão muitos desvios padrão longe da média - e menos quadrados e outros métodos de inferência estatística que são ideais para variáveis normalmente distribuídas muitas vezes se tornam altamente confiáveis quando aplicados a tais dados. Nesses casos, deve-se assumir uma distribuição mais pesada e aplicar-se os métodos de inferência estatística robustos adequados.
A distribuição gaussiana pertence à família das distribuições estáveis que são os atratores de somas de distribuições independentes e identicamente distribuídas, quer a média ou a variância seja finita ou não. Com exceção da gaussiana, que é um caso limite, todas as distribuições estáveis têm caudas pesadas e variância infinita. É uma das poucas distribuições estáveis e que possuem funções de densidade de probabilidade que podem ser expressas analiticamente, sendo as outras a distribuição de Cauchy e a distribuição de Lévy.
Simetrias e derivadas
A distribuição normal com densidade f(x)(x)} (Mean) μ μ - Sim. e desvio padrão 0}" xmlns="http://www.w3.org/1998/Math/MathML">σ σ >0- Sim.0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/762ecd0f0905dd0d4d7a07f80fa8bfb324b9b021" style="vertical-align: -0.338ex; width:5.591ex; height:2.176ex;"/>) tem as seguintes propriedades:
- É simétrico em torno do ponto x= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ ,Não. que é ao mesmo tempo o modo, a mediana e a média da distribuição.
- É unimodal: seu primeiro derivado é positivo para <math alttext="{displaystyle xx<μ μ ,- Sim.<img alt="{displaystyle x negativo para mu}" xmlns="http://www.w3.org/1998/Math/MathML">x>μ μ ,- Sim.
mu}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d3463a22382792e476326893bbc79d8ca5ed60c3" style="vertical-align: -0.838ex; width:6.477ex; height:2.343ex;"/> e zero apenas em x= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ .{displaystyle x=mu.}
- A área limitada pela curva e pela xNão.-axis é unidade (ou seja, igual a um).
- Seu primeiro derivado é f? ? (x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. x- Sim. - Sim. μ μ σ σ 2f(x).(x)=-{frac {x-mu }{sigma ^{2}}}f(x).}
- Sua densidade tem dois pontos de inflexão (onde o segundo derivado de fNão. é zero e mudança sinal), localizado um desvio padrão longe da média, ou seja, em x= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ - Sim. - Sim. σ σ {displaystyle x=mu -sigma } e x= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ +σ σ .{displaystyle x=mu +sigma.}
- Sua densidade é log-concave.
- Sua densidade é infinitamente diferenciável, de fato supersmooth da ordem 2.
Além disso, a densidade φ φ - Sim. da distribuição normal padrão (i.e. μ μ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle mu =0} e σ σ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1{displaystyle sigma} - Sim.) também tem as seguintes propriedades:
- Seu primeiro derivado é φ φ ? ? (x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. xφ φ (x).{displaystyle varphi ^{prime }(x)=-xvarphi (x).}
- Seu segundo derivado é φ φ ? ? ? ? (x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(x2- Sim. - Sim. 1)φ φ (x)(x)=(x^{2}-1)varphi (x)}
- Mais geralmente, sua no derivado é φ φ (n)(x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(- Sim. - Sim. 1)nEle.n (x)φ φ (x),{displaystyle varphi ^{(n)}(x)=(-1)^{n}operatorname {He} _{n}(x)varphi (x),} Onde? Ele.n (x){displaystyle operatorname {He} _{n}(x)} é o nth (probabilist) Hermite polinomial.
- A probabilidade de uma variável normalmente distribuída X- Sim. com conhecido μ μ - Sim. e σ σ - Sim. é em um conjunto particular, pode ser calculado usando o fato de que a fração Z.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(X- Sim. - Sim. μ μ )/σ σ {displaystyle Z=(X-mu)/sigma } tem uma distribuição normal padrão.
Momentos
Os momentos simples e absolutos de uma variável X- Sim. são os valores esperados de Xp{displaystyle X^{p}} e |X|p{displaystyle |X|^{p}}, respectivamente. Se o valor esperado μ μ - Sim. de X- Sim. é zero, estes parâmetros são chamados momentos centrais; caso contrário, estes parâmetros são chamados momentos não centrais. Normalmente estamos interessados apenas em momentos com ordem inteiro p{displaystyle p}.
Se X- Sim. tem uma distribuição normal, os momentos não centrais existem e são finitos para qualquer pNão. cuja parte real é maior que −1. Para qualquer inteiro não negativo pNão., os momentos centrais simples são:
- E Não.(X- Sim. - Sim. μ μ )p]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(0sepé estranho,σ σ p(p- Sim. - Sim. 1)!!sepé mesmo.{displaystyle operatorname {E} left[(X-mu)^{p}right]={begin{cases}0&{text{if }}p{text{ is odd,}}\sigma ^{p}(p-1)!&{text{if }}p{text{ is even.}}end{cases}}}
Aqui. n!!Não! denota o factorial duplo, ou seja, o produto de todos os números de nNão. a 1 que tem a mesma paridade n.Não.
Os momentos absolutos centrais coincidem com momentos simples para todas as ordens, mas são nonzero para ordens ímpares. Para qualquer inteiro não negativo p,Não.
- E Não.|X- Sim. - Sim. μ μ |p]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =σ σ p(p- Sim. - Sim. 1)!!)) (2D D sepé estranho1sepmesmo= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =σ σ p)) 2p/2)) (p+12)D D .{displaystyle {begin{aligned}operatorname} {E} left[|X-mu |^{p}right]&=sigma ^{p}(p-1)! cdot {begin{cases}{sqrt {frac {2}{pi }}}&{text{if }}p{text{ is odd}}1&{text{if }}p{text{ is even}}end{cases}}&=sigma ^{p}cdot {frac {2^{p/2}Gamma left({frac {p+1}{2}}
A última fórmula é válida também para qualquer não inteiro -1.}" xmlns="http://www.w3.org/1998/Math/MathML">p>- Sim. - Sim. 1.Não.-1.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/2664add830e3fdc570b1dddcdbe85950c3055332" style="vertical-align: -0.671ex; margin-left: -0.089ex; width:7.975ex; height:2.509ex;"/> Quando a média μ μ ≠ ≠ 0,{displaystyle mu neq 0,} os momentos simples e absolutos podem ser expressos em termos de funções hipergeométricas confluentes 1F1Não. {}_{1}F_{1}} e U.Não. U.
- E Não.Xp]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =σ σ p)) (- Sim. - Sim. Eu...2)pU(- Sim. - Sim. p2,12,- Sim. - Sim. 12(μ μ σ σ )2),E Não.|X|p]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =σ σ p)) 2p/2)) (1+p2)D D 1F1(- Sim. - Sim. p2,12,- Sim. - Sim. 12(μ μ σ σ )2).{displaystyle {begin{aligned}operatorname} {E} left[X^{p}right]&=sigma ^{p}cdot (-i{sqrt {2}})^{p}Uleft(-{frac {p}{2}},{frac {1}{2}},-{frac {1}{2}}left({frac {mu }{sigma }}right)^{2}right,\operatorname {E} left[|X|^{p}right]&=sigma ^{p}cdot 2^{p/2}{frac {Gamma left({frac {1+p}{2}}right)}{sqrt {pi }}}{}_{1}F_{1}left(-{frac {p}{2}},{frac {1}{2}},-{frac {1}{2}}left({frac {mu }{sigma }}right)^{2}right).end{aligned}}}
Estas expressões permanecem válidas mesmo se pNão. não é um inteiro. Veja também polinômios herméticos generalizados.
| Ordem | Momento não central | Hora central |
|---|---|---|
| 1 | μ μ - Sim. | 0Não. 0 |
| 2 | μ μ 2+σ σ 2{displaystyle mu ^{2}+sigma ^{2}} | σ σ 2{displaystyle sigma ^{2}} |
| 3 | μ μ 3+3μ μ σ σ 2{displaystyle mu ^{3}+3mu sigma ^{2}} | 0Não. 0 |
| 4 | μ μ 4+6μ μ 2σ σ 2+3σ σ 4{displaystyle mu ^{4}+6mu ^{2}sigma ^{2}+3sigma ^{4}} | 3σ σ 4{displaystyle 3sigma ^{4}} |
| 5 | μ μ 5+10.μ μ 3σ σ 2+15μ μ σ σ 4{displaystyle mu ^{5}+10mu ^{3}sigma ^{2}+15mu sigma ^{4}} | 0Não. 0 |
| 6 | μ μ 6+15μ μ 4σ σ 2+45μ μ 2σ σ 4+15σ σ 6{displaystyle mu ^{6}+15mu ^{4}sigma ^{2}+45mu ^{2}sigma ^{4}+15sigma ^{6}} | 15σ σ 6{displaystyle 15sigma ^{6}} |
| 7 | μ μ 7+21μ μ 5σ σ 2+105μ μ 3σ σ 4+105μ μ σ σ 6{displaystyle mu ^{7}+21mu ^{5}sigma ^{2}+105mu ^{3}sigma ^{4}+105mu sigma ^{6}} | 0Não. 0 |
| 8 | μ μ 8+28μ μ 6σ σ 2+210μ μ 4σ σ 4+420μ μ 2σ σ 6+105σ σ 8{displaystyle mu ^{8}+28mu ^{6}sigma ^{2}+210mu ^{4}sigma ^{4}+420mu ^{2}sigma ^{6}+105sigma ^{8}} | 105σ σ 8{displaystyle 105sigma ^{8}} |
A expectativa de X- Sim. condicionado no evento que X- Sim. está em um intervalo Não.um,b)]Não. é dado por
- <math alttext="{displaystyle operatorname {E} left[Xmid a<XE Não.X∣ ∣ um<X<b)]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ - Sim. - Sim. σ σ 2f(b))- Sim. - Sim. f(um)F(b))- Sim. - Sim. F(um){displaystyle operatorname {E} left[Xmid a<X<bright]=mu -sigma ^{2}{frac {f(b)-f(a)}{F(b)-F(a)}}}<img alt="{displaystyle operatorname {E} left[Xmid a<X
Onde? fNão. e FNão. respectivamente são a densidade e a função de distribuição cumulativa de X- Sim.. Para b)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∞ ∞ Não. Isto é conhecido como a relação Mills inversa. Note que acima, densidade fNão. de X- Sim. é usado em vez da densidade normal padrão como no inverso Taxa de moinhos, então aqui temos σ σ 2{displaystyle sigma ^{2}} em vez de σ σ - Sim..
Transformada de Fourier e função característica
A transformação de Fourier de uma densidade normal fNão. com média μ μ - Sim. e desvio padrão σ σ - Sim. o
- f^ ^ ())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ - Sim. - Sim. ∞ ∞ ∞ ∞ f(x)e- Sim. - Sim. Eu...)xDx= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =e- Sim. - Sim. Eu...μ μ )e- Sim. - Sim. 12(σ σ ))2{displaystyle {hat {f}}(t)=int _{-infty }^{infty }f(x)e^{-itx},dx=e^{-imu t}e^{-{frac {1}{2}}(sigma t)^{2}}}
Onde? Eu...Não. é a unidade imaginária. Se a média μ μ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle mu =0}, o primeiro fator é 1, e a transforma Fourier é, além de um fator constante, uma densidade normal no domínio de frequência, com média 0 e desvio padrão 1/σ σ - Não.. Em particular, a distribuição normal padrão φ φ - Sim. é um eigenfunction da transformação Fourier.
Em teoria da probabilidade, a transformação de Fourier da distribuição de probabilidade de uma variável aleatória de valor real X- Sim. está intimamente ligado à função característica φ φ X())(t)} dessa variável, que é definida como o valor esperado de eEu...)X{displaystyle e^{itX}}, como uma função da variável real )Não. (o parâmetro de frequência da transformação de Fourier). Esta definição pode ser analiticamente estendida a uma variável de valor complexo )Não.. A relação entre ambos é:
- φ φ X())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =f^ ^ (- Sim. - Sim. )){displaystyle varphi _{X}(t)={hat {f}}(-t)}
Funções geradoras de momentos e cumulantes
A função geradora de momento de uma variável aleatória real X- Sim. é o valor esperado de e)X{displaystyle e^{tX}}, como uma função do parâmetro real )Não.. Para uma distribuição normal com densidade fNão.Quero dizer... μ μ - Sim. e desvio σ σ - Sim., a função geradora de momento existe e é igual a
- M())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =E Não.e)X]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =f^ ^ (Eu...))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =eμ μ )e12σ σ 2)2{displaystyle M(t)=operatorname {E} [e^{tX}]={hat {f}}(it)=e^{mu t}e^{{tfrac {1}{2}}sigma ^{2}t^{2}}}
A função geradora cumulante é o logaritmo da função geradora de momento, ou seja
- g())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =I M())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ )+12σ σ 2)2{displaystyle g(t)=ln M(t)=mu t+{tfrac {1}{2}}sigma ^{2}t^{2}}
Uma vez que este é um polinomial quadrático em )Não., apenas os dois primeiros cumulants são nonzero, ou seja, a médiaμ μ - Sim. e a variânciaσ σ 2{displaystyle sigma ^{2}}.
Operador e classe de Stein
Dentro do método de Stein o operador Stein e classe de uma variável aleatória X∼ ∼ N(μ μ ,σ σ 2)Não. Xsim {mathcal {N}}(musigma ^{2})} são Af(x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =σ σ 2f?(x)- Sim. - Sim. (x- Sim. - Sim. μ μ )f(x){displaystyle {mathcal {A}}f(x)=sigma ^{2}f'(x)-(x-mu)f(x)} e F{displaystyle {mathcal {F}}} a classe de todas as funções absolutamente contínuas <math alttext="{displaystyle f:mathbb {R} to mathbb {R} {mbox{ such that }}mathbb {E} [|f'(X)|]f:R→ → Rtal queENão.|f?(X)|]<∞ ∞ {displaystyle f:mathbb] {R} to mathbb {R} {mbox{ such that }}mathbb {E} [|f'(X)|infty }<img alt="{displaystyle f:mathbb {R} to mathbb {R} {mbox{ such that }}mathbb {E} [|f'(X)|].
Limite de variância zero
No limite quando σ σ - Sim. tende a zero, a densidade de probabilidade f(x)(x)} eventualmente tende a zero em qualquer x≠ ≠ μ μ {displaystyle xneq mu }, mas cresce sem limite se x= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ - Sim., enquanto sua integral permanece igual a 1. Portanto, a distribuição normal não pode ser definida como uma função comum quando σ σ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle sigma=0}.
No entanto, pode-se definir a distribuição normal com zero variância como uma função generalizada; especificamente, como "função delta" de Dirac δ δ - Sim. traduzido pela média μ μ - Sim., isto é f(x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =δ δ (x- Sim. - Sim. μ μ ).{displaystyle f(x)=delta (x-mu). ?Seu CDF é então a função passo pesado traduzida pela média μ μ - Sim.,
- <math alttext="{displaystyle F(x)={begin{cases}0&{text{if }}xF(x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(0sex<μ μ 1sex≥ ≥ μ μ {displaystyle F(x)={begin{cases}0&{text{if }}x<mu \1&{text{if }}xgeq mu end{cases}}}<img alt="{displaystyle F(x)={begin{cases}0&{text{if }}x
Entropia máxima
De todas as distribuições de probabilidade sobre os reais com uma média especificada μ μ - Sim. e variânciaσ σ 2{displaystyle sigma ^{2}}, a distribuição normal N(μ μ ,σ σ 2){displaystyle N(musigma ^{2})} é aquele com entropia máxima. Se X- Sim. é uma variável aleatória contínua com densidade de probabilidade f(x)(x)}, então a entropia de X- Sim. é definido como
- H. H. H.(X)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. ∫ ∫ - Sim. - Sim. ∞ ∞ ∞ ∞ f(x)log f(x)Dx{displaystyle H(X)=-int _{-infty }^{infty }f(x)log f(x),dx}
Onde? f(x)log f(x){displaystyle f(x)log f(x)} é entendido como zero sempre f(x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0(x)=0}. Este funcional pode ser maximizado, sujeito às restrições que a distribuição é adequadamente normalizada e tem uma variância especificada, usando cálculo variacional. Uma função com dois multiplicadores Lagrange é definida:
- L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ - Sim. - Sim. ∞ ∞ ∞ ∞ f(x)I (f(x))Dx- Sim. - Sim. λ λ 0(1- Sim. - Sim. ∫ ∫ - Sim. - Sim. ∞ ∞ ∞ ∞ f(x)Dx)- Sim. - Sim. λ λ (σ σ 2- Sim. - Sim. ∫ ∫ - Sim. - Sim. ∞ ∞ ∞ ∞ f(x)(x- Sim. - Sim. μ μ )2Dx){displaystyle L=int _{-infty }^{infty }f(x)ln(f(x)),dx-lambda _{0}left(1-int _{-infty }^{infty }f(x),dxright)-lambda left(sigma ^{2}-int
Onde? f(x)(x)} é, por enquanto, considerado como uma função de densidade com média μ μ - Sim. e desvio padrão σ σ - Sim..
Na entropia máxima, uma pequena variação δ δ f(x)(x)} sobre f(x)(x)} produzirá uma variação δ δ L- Sim. sobre LNão. L. que é igual a 0:
- 0= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =δ δ L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ - Sim. - Sim. ∞ ∞ ∞ ∞ δ δ f(x)(I (f(x))+1+λ λ 0+λ λ (x- Sim. - Sim. μ μ )2)Dx{displaystyle 0=delta L=int _{-infty }^{infty }delta f(x)left(ln(f(x))+1+lambda _{0}+lambda (x-mu)^{2}right),dx}
Uma vez que isso deve segurar qualquer pequeno δ δ f(x)(x)}, o termo entre parênteses deve ser zero, e resolver para f(x)(x)} Rendimentos:
- f(x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =e- Sim. - Sim. λ λ 0- Sim. - Sim. 1- Sim. - Sim. λ λ (x- Sim. - Sim. μ μ )2{displaystyle f(x)=e^{-lambda _{0}-1-lambda (x-mu)^{2}}}
Usando as equações de restrição para resolver λ λ 0{displaystyle lambda _{0}} e λ λ - Sim. produz a densidade da distribuição normal:
- f(x,μ μ ,σ σ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12D D σ σ 2e- Sim. - Sim. (x- Sim. - Sim. μ μ )22σ σ 2{displaystyle f(x,musigma)={frac {1}{sqrt {2pi sigma ^{2}}^{-{frac {(x-mu)^{2}}{2sigma ^{2}}}}
A entropia de uma distribuição normal é igual a
- H. H. H.(X)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12(1+I (2σ σ 2D D )){displaystyle H(X)={tfrac {1}{2}}(1+ln(2sigma ^{2}pi)}
Outras propriedades
- Se a função característica φ φ X{displaystyle phi _{X}} de alguma variável aleatória X- Sim. é da forma φ φ X())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =expQ()){displaystyle phi _{X}(t)=exp ^{Q(t)}}, onde Q())(T)} é um polinômio, então o Marcinkiewicz teorema (nomeado após Józef Marcinkiewicz) afirma que QNão. pode ser no máximo um polinômio quadrático, e, portanto, X- Sim. é uma variável aleatória normal. A consequência deste resultado é que a distribuição normal é a única distribuição com um número finito (dois) de cumulants não-zero.
- Se X- Sim. e YNão. Sim. são comuns normais e não-cor-relacionadas, então eles são independentes. A exigência de que X- Sim. e YNão. Sim. deve ser em conjunto normal é essencial; sem ele a propriedade não segura.[prova] Para variáveis aleatórias não-normais a uncorrelatedness não implica independência.
- A divergência Kullback–Leibler de uma distribuição normal X1∼ ∼ N(μ μ 1,σ σ 12){displaystyle X_{1}sim N(mu _{1},sigma _{1}^{2})} de outro X2∼ ∼ N(μ μ 2,σ σ 22){displaystyle X_{2}sim N(mu _{2},sigma _{2}^{2})} é dado por: A distância do Hellinger entre as mesmas distribuições é igual aDKKL(X1‖ ‖ X2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(μ μ 1- Sim. - Sim. μ μ 2)22σ σ 22+12(σ σ 12σ σ 22- Sim. - Sim. 1- Sim. - Sim. I σ σ 12σ σ 22){displaystyle D_{mathrm {KL} }(X_{1},|,X_{2})={frac {(mu _{1}-mu _{2})^{2}}{2sigma _{2}^{2}}}+{frac {1}{2}}left({frac _{1}^{2}} _{2}^{2}}}-1-ln _{1}^{2}} _{2}^{2}}}right)}H. H. H.2(X1,X2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1- Sim. - Sim. 2σ σ 1σ σ 2σ σ 12+σ σ 22e- Sim. - Sim. 14(μ μ 1- Sim. - Sim. μ μ 2)2σ σ 12+σ σ 22{displaystyle H^{2}(X_{1},X_{2})=1-{sqrt {frac {2sigma _{1}sigma _{2}} _{1}^{2}+sigma _{2}^{2}}}}e^{-{frac {1}{4}}{frac {(mu _{1}-mu _{2})^{2}}{sigma _{1}^{2}+sigma _{2}^{2}}}
- A matriz de informação Fisher para uma distribuição normal w.r.t. μ μ - Sim. e σ σ 2{displaystyle sigma ^{2}} é diagonal e toma a forma Eu...(μ μ ,σ σ 2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(1σ σ 20012σ σ 4){displaystyle {mathcal {I}}(musigma ^{2})={begin{pmatrix}{frac {1}{sigma ^{2}}}&0\&{frac {1}{2sigma ^{4}}}end{pmatrix}}}
- O conjugado antes da média de uma distribuição normal é outra distribuição normal. Especificamente, se x1,...... ,xn{displaystyle x_{1},ldotsx_{n}} são id ∼ ∼ N(μ μ ,σ σ 2){displaystyle sim N(musigma ^{2})} e o anterior é μ μ ∼ ∼ N(μ μ 0,σ σ 02){displaystyle mu sim N(mu _{0},sigma _{0}^{2})}, então a distribuição posterior para o estimador de μ μ - Sim. será μ μ ∣ ∣ x1,...... ,xn∼ ∼ N(σ σ 2nμ μ 0+σ σ 02x? ? σ σ 2n+σ σ 02,(nσ σ 2+1σ σ 02)- Sim. - Sim. 1){displaystyle mu mid x_{1},ldotsx_{n}sim {mathcal {N}}left({frac {{frac} Sim. ^{2}}{n}}mu _{0}+sigma _{0}^{2}{bar Não. Sim. ^{2}}{n}}+sigma _{0}^{2}}},left({frac Não. ^{2}}}+{frac Não. _{0}^{2}}}right)^{-1}right)}
- A família de distribuições normais não só forma uma família exponencial (EF), mas de fato forma uma família exponencial natural (NEF) com função de variância quadrática (NEF-QVF). Muitas propriedades de distribuições normais generalizam-se em propriedades de distribuições NEF-QVF, distribuições NEF ou distribuições EF geralmente. As distribuições NEF-QVF compreendem 6 famílias, incluindo Poisson, Gamma, binomial e distribuições binomiais negativas, enquanto muitas das famílias comuns estudadas em probabilidade e estatísticas são NEF ou EF.
- Na geometria da informação, a família de distribuições normais forma um coletor estatístico com curvatura constante - Sim. - Sim. 1Não. -1. A mesma família é plana com relação às conexões (±1) ? ? (e){displaystyle nabla ^{(e)}} e ? ? (m){displaystyle nabla ^{(m)}}.
Distribuições relacionadas
Teorema do limite central

O teorema do limite central indica que, em determinadas condições (justamente comuns), a soma de muitas variáveis aleatórias terá uma distribuição aproximadamente normal. Mais especificamente, onde X1,...... ,Xn{displaystyle X_{1},ldots X_{n}} são variáveis aleatórias independentes e distribuídas de forma idêntica com a mesma distribuição arbitrária, média zero e variância σ σ 2{displaystyle sigma ^{2}} e Z.Não. eles são escalada média por n- Sim.
- Z.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =n(1nGerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nXEu...){displaystyle Z={sqrt {n}}left({frac {1}{n}}sum _{i=1}^{n}X_{i}right)}
Então, como nNão. aumentos, a distribuição de probabilidade Z.Não. tenderá a distribuição normal com média zero e variância σ σ 2{displaystyle sigma ^{2}}.
O teorema pode ser estendido para variáveis (XEu...)(X_{i})} que não são independentes e/ou não distribuídos de forma idêntica se certas restrições forem colocadas no grau de dependência e nos momentos das distribuições.
Muitas estatísticas de teste, pontuações e estimadores encontrados na prática contêm somas de certas variáveis aleatórias neles, e ainda mais estimadores podem ser representados como somas de variáveis aleatórias por meio do uso de funções de influência. O teorema do limite central implica que esses parâmetros estatísticos terão distribuições assintoticamente normais.
O teorema do limite central também implica que certas distribuições podem ser aproximadas pela distribuição normal, por exemplo:
- A distribuição binomial B(n,p)(n,p)} é aproximadamente normal com média npNão. e variância np(1- Sim. - Sim. p){displaystyle np(1-p)} para grande nNão. e para pNão. não muito perto de 0 ou 1.
- A distribuição de Poisson com parâmetro λ λ - Sim. é aproximadamente normal com média λ λ - Sim. e variância λ λ - Sim., para grandes valores de λ λ - Sim..
- A distribuição qui-quadrado χ χ 2(k)(k)} é aproximadamente normal com média kNão. e variância 2k- Sim., para grande kNão..
- A distribuição t do estudante )(Processo Processo ){displaystyle t(nu)} é aproximadamente normal com média 0 e variância 1 quando Processo Processo Não. é grande.
Se essas aproximações são suficientemente precisas depende da finalidade para a qual são necessárias e da taxa de convergência para a distribuição normal. Normalmente, essas aproximações são menos precisas nas extremidades da distribuição.
Um limite superior geral para o erro de aproximação no teorema do limite central é dado pelo teorema de Berry–Esseen, melhorias na aproximação são dadas pelas expansões de Edgeworth.
Este teorema também pode ser usado para justificar a modelagem da soma de muitas fontes uniformes de ruído como ruído gaussiano. Veja AWGN.
Operações e funções de variáveis normais

A densidade de probabilidade, distribuição cumulativa e distribuição cumulativa inversa de qualquer função de uma ou mais variáveis normais independentes ou correlacionadas podem ser calculadas com o método numérico de rastreamento de raios (código Matlab). Nas seções a seguir, veremos alguns casos especiais.
Operações em uma única variável normal
Se X- Sim. é distribuído normalmente com média μ μ - Sim. e variância σ σ 2{displaystyle sigma ^{2}}, então
- umX+b)Não. AX+b, para qualquer número real umNão. e b)Não., também é normalmente distribuído, com média umμ μ +b){displaystyle amu +b} e desvio padrão |um|σ σ |a|sigma }. Ou seja, a família de distribuições normais é fechada sob transformações lineares.
- A exponencial X- Sim. é distribuído de forma normal: eX∼ ∼ I (N(μ μ ,σ σ 2)){displaystyle e^{X}sim ln(N(musigma ^{2})}).
- O valor absoluto de X- Sim. tem distribuição normal dobrada: |X|∼ ∼ Nf(μ μ ,σ σ 2){displaystyle {left|Xright|sim N_{f}(musigma ^{2})}}. Se μ μ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle mu =0} isto é conhecido como a distribuição meio-normal.
- O valor absoluto dos resíduos normalizados, |X- Sim. - Sim. μ μ |/σ σ |X-mu |/sigma }, tem distribuição chi com um grau de liberdade: |X- Sim. - Sim. μ μ |/σ σ ∼ ∼ χ χ 1|X-mu |/sigma sim chi _{1}}.
- O quadrado de X/σ σ - Sim. tem a distribuição de qui-quadrado não central com um grau de liberdade: X2/σ σ 2∼ ∼ χ χ 12(μ μ 2/σ σ 2)Não. X^{2}/sigma ^{2}sim chi _{1}^{2}(mu ^{2}/sigma ^{2})}. Se μ μ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle mu =0}, a distribuição é chamada simplesmente chi-quadrado.
- O log-likelihood de uma variável normal xNão. é simplesmente o log de sua função de densidade de probabilidade: Uma vez que este é um quadrado escalado e deslocado de uma variável normal padrão, ele é distribuído como uma variável escalada e deslocada chi-quadrado.I p(x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 12(x- Sim. - Sim. μ μ σ σ )2- Sim. - Sim. I (σ σ 2D D )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 12zangão.2- Sim. - Sim. I (σ σ 2D D ).{displaystyle ln p(x)=-{frac {1}{2}}left({frac {x-mu) }{sigma }}right)^{2}-ln left(sigma {sqrt {2pi }}right)=-{frac {1}{2}}z^{2}-ln left(sigma {sqrt {2pi }}right). ?
- Distribuição da variável X- Sim. restrito a um intervalo Não.um,b)]Não. é chamado de distribuição normal truncada.
- (X- Sim. - Sim. μ μ )- Sim. - Sim. 2(X-mu)^{-2}} tem uma distribuição Lévy com localização 0 e escala σ σ - Sim. - Sim. 2{displaystyle sigma ^{-2}}.
Operações em duas variáveis normais independentes
- Se X1{displaystyle X_{1}} e X2{displaystyle X_{2}} são duas variáveis aleatórias normais independentes, com meios μ μ 1{displaystyle mu _{1}}, μ μ 2{displaystyle mu _{2}} e desvios padrão σ σ 1{displaystyle sigma} _{1}}, σ σ 2{displaystyle sigma _{2}}, então a sua soma X1+X2Não. X_{1}+X_{2}} também será normalmente distribuído,[prova] com média μ μ 1+μ μ 2{displaystyle mu _{1}+mu _{2}} e variância σ σ 12+σ σ 22Não. _{1}^{2}+sigma _{2}^{2}}.
- Em particular, se X- Sim. e YNão. Sim. são desvios normais independentes com média zero e variância σ σ 2{displaystyle sigma ^{2}}, então X+YNão. X+Y e X- Sim. - Sim. Y- Sim. são também independentes e normalmente distribuídos, com média zero e variância 2σ σ 2{displaystyle 2sigma ^{2}}. Este é um caso especial da identidade de polarização.
- Se X1{displaystyle X_{1}}, X2{displaystyle X_{2}} são dois desvios normais independentes com média μ μ - Sim. e desvio σ σ - Sim.e umNão., b)Não. são números reais arbitrários, então a variável também é normalmente distribuído com média μ μ - Sim. e desvio σ σ - Sim.. Segue-se que a distribuição normal é estável (com expoente) α α = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2{displaystyle alfa =2).X3= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =umX1+b)X2- Sim. - Sim. (um+b))μ μ um2+b)2+μ μ Não. X_{3}={frac {aX_{1}+bX_{2}-(a+b)mu }{sqrt {a^{2}+b^{2}}+mu ?
Operações em duas variáveis normais padrão independentes
Se X1{displaystyle X_{1}} e X2{displaystyle X_{2}} são duas variáveis aleatórias normais padrão independentes com média 0 e variância 1, então
- Sua soma e diferença é distribuída normalmente com média zero e variância dois: X1± ± X2∼ ∼ N(0,2)Não. X_{1}pm X_{2}sim {mathcal {N}}(0,2)}.
- O seu produto Z.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =X1X2Não. Z=X_{1}X_{2}} segue a distribuição do produto com função de densidade fZ.(zangão.)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =D D - Sim. - Sim. 1KK0(|zangão.|){displaystyle f_{Z}(z)=pi ^{-1}K_{0}(|z|)} Onde? KK0Não. K_{0}} é a função Bessel modificada do segundo tipo. Esta distribuição é simétrica em torno de zero, não ultrapassada zangão.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0- Sim., e tem a função característica φ φ Z.())= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(1+)2)- Sim. - Sim. 1/2{displaystyle phi _{Z}(t)=(1+t^{2})^{-1/2}}.
- Sua relação segue a distribuição padrão Cauchy: X1/X2∼ ∼ Cauda (0,1)Não. X_{1}/X_{2}sim operatorname (0,1).
- Sua norma Euclidiana X12+X22{displaystyle {sqrt {X_{1}^{2}+X_{2}^{2}}}} tem a distribuição Rayleigh.
Operações em múltiplas variáveis normais independentes
- Any linear combination of independent normal deviates is a normal deviate.
- If
X
1
,
X
2
,
…
,
X
n
{displaystyle X_{1},X_{2},ldotsX_{n}}
are independent standard normal random variables, then the sum of their squares has the chi-squared distribution with
n
{displaystyle n}
degrees of freedom X 1 2 + ⋯ + X n 2 ∼ χ n 2 . {displaystyle X_{1}^{2}+cdots +X_{n}^{2}sim chi _{n}^{2}.}
- If
X
1
,
X
2
,
…
,
X
n
{displaystyle X_{1},X_{2},ldotsX_{n}}
are independent normally distributed random variables with means
μ
{displaystyle mu }
and variances
σ
2
{displaystyle sigma ^{2}}
, then their sample mean is independent from the sample standard deviation, which can be demonstrated using Basu's theorem or Cochran's theorem. The ratio of these two quantities will have the Student's t-distribution with
n
−
1
{displaystyle n-1}
degrees of freedom: t = X ¯ − μ S / n = 1 n ( X 1 + ⋯ + X n ) − μ 1 n ( n − 1 ) [ ( X 1 − X ¯ ) 2 + ⋯ + ( X n − X ¯ ) 2 ] ∼ t n − 1 . {displaystyle t={frac {{overline {X}}-mu }{S/{sqrt {n}}}}={frac {{frac {1}{n}}(X_{1}+cdots +X_{n})-mu }{sqrt {{frac {1}{n(n-1)}}left[(X_{1}-{overline {X}})^{2}+cdots +(X_{n}-{overline {X}})^{2}right]}}}sim t_{n-1}.}
- If
X
1
,
X
2
,
…
,
X
n
{displaystyle X_{1},X_{2},ldotsX_{n}}
,
Y
1
,
Y
2
,
…
,
Y
m
{displaystyle Y_{1},Y_{2},ldotsY_{m}}
are independent standard normal random variables, then the ratio of their normalized sums of squares will have the F-distribution with (n, m) degrees of freedom: F = ( X 1 2 + X 2 2 + ⋯ + X n 2 ) / n ( Y 1 2 + Y 2 2 + ⋯ + Y m 2 ) / m ∼ F n , m . {displaystyle F={frac {left(X_{1}^{2}+X_{2}^{2}+cdots +X_{n}^{2}right)/n}{left(Y_{1}^{2}+Y_{2}^{2}+cdots +Y_{m}^{2}right)/m}}sim F_{n,m}.}
Operações em múltiplas variáveis normais correlacionadas
- Uma forma quadrática de um vetor normal, ou seja, uma função quadrática q= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento xEu...2+Gerenciamento Gerenciamento xJJ+c- Sim. x_{i}^{2}+sum x_{j}+c} de múltiplas variáveis normais independentes ou correlacionadas, é uma variável qui-quadrado generalizada.
Operações na função de densidade
A distribuição normal dividida é definida mais diretamente em termos de junção de seções dimensionadas das funções de densidade de diferentes distribuições normais e redimensionamento da densidade para integrar a uma. A distribuição normal truncada resulta do redimensionamento de uma seção de uma única função de densidade.
Divisibilidade infinita e teorema de Cramér
Para qualquer inteiro positivo n- Sim., qualquer distribuição normal com média μ μ - Sim. e variância σ σ 2{displaystyle sigma ^{2}} é a distribuição da soma de n- Sim. desvios normais independentes, cada um com média μ μ n- Não. ? e variância σ σ 2n{displaystyle {frac {sigma ^{2}}{n}}}}}}. Esta propriedade é chamada de divisibilidade infinita.
Por outro lado, se X1{displaystyle X_{1}} e X2{displaystyle X_{2}} são variáveis aleatórias independentes e sua soma X1+X2Não. X_{1}+X_{2}} tem uma distribuição normal, então ambos X1{displaystyle X_{1}} e X2{displaystyle X_{2}} devem ser desvios normais.
Esse resultado é conhecido como teorema da decomposição de Cramér e equivale a dizer que a convolução de duas distribuições é normal se e somente se ambas forem normais. O teorema de Cramér implica que uma combinação linear de variáveis não gaussianas independentes nunca terá uma distribuição exatamente normal, embora possa aproximá-la arbitrariamente.
Teorema de Bernstein
O teorema de Bernstein afirma que se X- Sim. e YNão. Sim. são independentes e X+YNão. X+Y e X- Sim. - Sim. Y- Sim. também são independentes, então ambos X e Y deve necessariamente ter distribuições normais.
Mais geralmente, se X1,...... ,Xn{displaystyle X_{1},ldots X_{n}} são variáveis aleatórias independentes, então duas combinações lineares distintas Gerenciamento Gerenciamento umkXk- Sim. {a_{k}X_{k}}} e Gerenciamento Gerenciamento b)kXk- Sim. {b_{k}X_{k}}}será independente se e somente se tudo XkNão. X_{k}} são normais e Gerenciamento Gerenciamento umkb)kσ σ k2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0- Sim. {a_{k}b_{k}sigma _{k}^{2}=0}}, onde σ σ k2{displaystyle sigma _{k}^{2}} denota a variância de XkNão. X_{k}}.
Extensões
A noção de distribuição normal, sendo uma das distribuições mais importantes na teoria da probabilidade, foi estendida muito além da estrutura padrão do caso univariado (ou seja, unidimensional) (Caso 1). Todas essas extensões também são chamadas de leis normais ou Gaussianas, então existe uma certa ambigüidade nos nomes.
- A distribuição normal multivariada descreve a lei gaussiana na k-dimensional Espaço euclidiano. Um vetor X ∈ Rk é multivariada-normalmente distribuída se qualquer combinação linear de seus componentes Σk
JJ= 1umJJ XJJ tem uma distribuição normal (univariada). A variância de X é um k × k matriz positiva definida simétricaV. A distribuição normal multivariada é um caso especial das distribuições elípticas. Como tal, seu loci iso-densidade no k = 2 caso são elipses e no caso de arbitrário k são elipsoides. - Distribuição Gaussiana retificada uma versão retificada da distribuição normal com todos os elementos negativos redefinidos para 0
- A distribuição normal complexa lida com os vetores normais complexos. Um vetor complexo X ∈ Ck é dito ser normal se ambos os seus componentes reais e imaginários possuem conjuntamente um 2k- distribuição normal multivariada dimensional. A estrutura de variância-covariância X é descrito por duas matrizes: o variância matriz Γ, e relação matriz de matrizC.
- A distribuição normal da matriz descreve o caso de matrizes normalmente distribuídas.
- Os processos gaussianos são os processos estocásticos normalmente distribuídos. Estes podem ser vistos como elementos de algum espaço de Hilbert infinita-dimensionalH. H. H., e assim são os análogos de vetores normais multivariados para o caso k = ∞. Um elemento aleatório h ∈ H. H. H. é dito ser normal se para qualquer constante um ∈ H. H. H. o produto escalar (um, h) tem uma distribuição normal (univariada). A estrutura de variância de tal elemento aleatório gaussiano pode ser descrita em termos de linear covariância operador K: H → H. Vários processos gaussianos tornaram-se populares o suficiente para ter seus próprios nomes:
- Movimento browniano,
- Ponte Browniana,
- Processo Ornstein-Uhlenbeck.
- Gaussian q-distribution é uma construção matemática abstrata que representa um "q-analogue" da distribuição normal.
- o q-Gaussian é um análogo da distribuição gaussiana, no sentido de que maximiza a entropia de Tsallis, e é um tipo de distribuição de Tsallis. Note que esta distribuição é diferente da distribuição Gaussian q acima.
- A distribuição Kaniadakis κ-Gaussian é uma generalização da distribuição gaussiana que surge das estatísticas de Kaniadakis, sendo uma das distribuições de Kaniadakis.
Uma variável aleatória X tem uma distribuição normal de duas partes se tiver uma distribuição
- fX(x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =N(μ μ ,σ σ 12)sex≤ ≤ μ μ {displaystyle f_{X}(x)=N(musigma _{1}^{2}){text{ if }}xleq mu }
- fX(x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =N(μ μ ,σ σ 22)sex≥ ≥ μ μ {displaystyle f_{X}(x)=N(musigma _{2}^{2}){text{ if }}xgeq mu }
onde μ é a média e σ 1 e σ Os desvios padrão da distribuição à esquerda e à direita da média, respectivamente.
A média, variação e terceiro momento central desta distribuição foram determinados
- E (X)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ +2D D (σ σ 2- Sim. - Sim. σ σ 1){displaystyle operatorname} (E} (X)=mu +{sqrt {2}{pi }}}(sigma _{2}-sigma _{1}
- V (X)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(1- Sim. - Sim. 2D D )(σ σ 2- Sim. - Sim. σ σ 1)2+σ σ 1σ σ 2{displaystyle operatorname} {V} (X)=left(1-{frac {2}{pi }}right)(sigma _{2}-sigma _{1})^{2}+sigma _{1}sigma _{2}}
- T (X)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2D D (σ σ 2- Sim. - Sim. σ σ 1)Não.(4D D - Sim. - Sim. 1)(σ σ 2- Sim. - Sim. σ σ 1)2+σ σ 1σ σ 2]{displaystyle operatorname} {T} (X)={sqrt {frac {2}{pi }}}(sigma _{2}-sigma _{1})left[left({frac {4}{pi }}-1right)(sigma _{2}-sigma _{1})^{2}+sigma _{1}sigma _{2}right]}
onde E(X), V(X) e T(X) são a média, a variância e o terceiro momento central, respectivamente.
Um dos principais usos práticos da lei gaussiana é modelar as distribuições empíricas de muitas variáveis aleatórias diferentes encontradas na prática. Nesse caso, uma extensão possível seria uma família de distribuições mais rica, com mais de dois parâmetros e, portanto, capaz de ajustar a distribuição empírica com mais precisão. Os exemplos de tais extensões são:
- Distribuição de Pearson — uma família de quatro parâmetros de distribuições de probabilidade que estendem a lei normal para incluir diferentes valores de cegueira e kurtosis.
- A distribuição normal generalizada, também conhecida como distribuição de energia exponencial, permite caudas de distribuição com comportamentos assintóticos mais grossos ou mais finos.
Inferência estatística
Estimativa de parâmetros
É muitas vezes o caso de não sabermos os parâmetros da distribuição normal, mas em vez disso queremos estima-los. Ou seja, ter uma amostra (x1,...... ,xn)(x_{1},ldotsx_{n})} de um normal N(μ μ ,σ σ 2){displaystyle {mathcal {N}}(musigma ^{2})} população que gostaríamos de aprender os valores aproximados de parâmetros μ μ - Sim. e σ σ 2{displaystyle sigma ^{2}}. A abordagem padrão para este problema é o método de máxima probabilidade, que requer maximização do função de verificação:
- I L(μ μ ,σ σ 2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nI f(xEu...∣ ∣ μ μ ,σ σ 2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. n2I (2D D )- Sim. - Sim. n2I σ σ 2- Sim. - Sim. 12σ σ 2Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n(xEu...- Sim. - Sim. μ μ )2.{displaystyle ln {mathcal {L}}(musigma ^{2})=sum _{i=1}^{n}ln f(x_{i}mid musigma ^{2})=-{frac {n}{2}}ln(2pi)-{frac {n}{2}}ln sigma ^{2}-{frac {1}{2sigma ^{2}}}sum _{i=1}^{n}(x_{i}-mu)^{2}.}
Tomando derivados em relação a μ μ - Sim. e σ σ 2{displaystyle sigma ^{2}} e resolver o sistema resultante de condições de primeira ordem produz o estimativas máximas de probabilidade:
- μ μ ^ ^ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =x? ? )) 1nGerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nxEu...,σ σ ^ ^ 2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nGerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n(xEu...- Sim. - Sim. x? ? )2.- Não. }}={overline {x}}equiv {frac {1}{n}}sum _{i=1}^{n}x_{i},qquad Não. }}^{2}={frac {1}{n}}sum _{i=1}^{n}(x_{i}-{overline {x}})^{2}.
Média da amostra
Estimador μ μ ^ ^ {displaystyle textstyle {hat {mu}) é chamado de amostra média, uma vez que é o meio aritmético de todas as observações. A estatística x? ? {displaystyle textstyle {overline {x}}} é completo e suficiente para μ μ - Sim., e, portanto, pelo teorema de Lehmann-Scheffé, μ μ ^ ^ {displaystyle textstyle {hat {mu}) é a variância mínima uniformemente imparcial (UMVU) estimador. Em amostras finitas é distribuído normalmente:
- μ μ ^ ^ ∼ ∼ N(μ μ ,σ σ 2/n).{displaystyle {hat {mu }}sim {mathcal {N}}(musigma ^{2}/n).}
A variância deste estimador é igual à μμ-elemento da matriz de informação Fisher inversa Eu...- Sim. - Sim. 1{displaystyle textstyle {mathcal {I}}^{-1}}. Isso implica que o estimador é eficiente em amostra finita. De importância prática é o fato de que o erro padrão de μ μ ^ ^ {displaystyle textstyle {hat {mu}) é proporcional a 1/n{displaystyle textstyle 1/{sqrt {n}}}, isto é, se quisermos diminuir o erro padrão por um fator de 10, deve-se aumentar o número de pontos na amostra por um fator de 100. Este fato é amplamente utilizado na determinação de tamanhos de amostra para pesquisas de opinião e o número de testes em simulações de Monte Carlo.
Do ponto de vista da teoria assintótica, μ μ ^ ^ {displaystyle textstyle {hat {mu}) é consistente, ou seja, converge na probabilidade de μ μ - Sim. como n→ → ∞ ∞ {displaystyle nrightarrow infty }. O estimador também é assintoticamente normal, que é um simples corolário do fato de que é normal em amostras finitas:
- n(μ μ ^ ^ - Sim. - Sim. μ μ )→DN(0,σ σ 2).{displaystyle {sqrt {n}}({hat {mu }}-mu),{xrightarrow {d}},{mathcal {N}}(0,sigma ^{2}). ?
Variação da amostra
O estimador σ σ ^ ^ 2{displaystyle textstyle {hat {sigma }}^{2}} é chamado de variância de amostra, uma vez que é a variância da amostra ((x1,...... ,xn)(x_{1},ldotsx_{n})}). Na prática, outro estimador é frequentemente usado em vez do σ σ ^ ^ 2{displaystyle textstyle {hat {sigma }}^{2}}. Este outro estimador é denotado S2{displaystyle s^{2}}, e também é chamado de variância de amostra, que representa uma certa ambiguidade na terminologia; sua raiz quadrada SNão. é chamado de desvio padrão da amostra. O estimador S2{displaystyle s^{2}} difere de σ σ ^ ^ 2{displaystyle textstyle {hat {sigma }}^{2}} por ter (n - 1) em vez den no denominador (a chamada correção de Bessel):
- S2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =nn- Sim. - Sim. 1σ σ ^ ^ 2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n- Sim. - Sim. 1Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n(xEu...- Sim. - Sim. x? ? )2.Não. S04E18 Não. Sim. }}^{2}={frac {1}{n-1}sum _{i=1}^{n}(x_{i}-{overline {x}})^{2}.
A diferença entre S2{displaystyle s^{2}} e σ σ ^ ^ 2{displaystyle textstyle {hat {sigma }}^{2}} torna-se negligivelmente pequeno para grande n'S. Em amostras finitas no entanto, a motivação por trás do uso de S2{displaystyle s^{2}} é que é um estimador imparcial do parâmetro subjacente σ σ 2{displaystyle sigma ^{2}}, Considerando que σ σ ^ ^ 2{displaystyle textstyle {hat {sigma }}^{2}} é tendencioso. Além disso, pelo teorema de Lehmann-Scheffé o estimador S2{displaystyle s^{2}} é uniformemente variância mínima imparcial (UMVU), o que o torna o "melhor" estimador entre todos os imparciais. No entanto, pode-se mostrar que o estimador tendencioso σ σ ^ ^ 2{displaystyle textstyle {hat {sigma }}^{2}} é "melhor" do que o S2{displaystyle s^{2}} em termos do critério de erro quadrado médio (MSE). Em amostras finitas ambos S2{displaystyle s^{2}} e σ σ ^ ^ 2{displaystyle textstyle {hat {sigma }}^{2}} ter escalado qui-quadrado distribuição com (n - 1) graus de liberdade:
- S2∼ ∼ σ σ 2n- Sim. - Sim. 1)) χ χ n- Sim. - Sim. 12,σ σ ^ ^ 2∼ ∼ σ σ 2n)) χ χ n- Sim. - Sim. 12.{displaystyle s^{2}sim} {frac - Sim. chi _{n-1}^{2},qquad {hat {sigma }}^{2}sim {frac {displaystyle ^{2}}{n}}cdot chi _{n-1}^{2}.}
A primeira dessas expressões mostra que a variância de S2{displaystyle s^{2}} é igual a 2σ σ 4/(n- Sim. - Sim. 1)(n-1)}, que é ligeiramente maior do que o σ-elemento da matriz de informação Fisher inversa Eu...- Sim. - Sim. 1{displaystyle textstyle {mathcal {I}}^{-1}}. Assim, S2{displaystyle s^{2}} não é um estimador eficiente para σ σ 2{displaystyle sigma ^{2}}, e além disso, desde S2{displaystyle s^{2}} é UMVU, podemos concluir que o estimador eficiente de amostra finita para σ σ 2{displaystyle sigma ^{2}} não existe.
Aplicando a teoria assintótica, ambos os estimadores S2{displaystyle s^{2}} e σ σ ^ ^ 2{displaystyle textstyle {hat {sigma }}^{2}} são consistentes, ou seja, convergem na probabilidade de σ σ 2{displaystyle sigma ^{2}} como o tamanho da amostra n→ → ∞ ∞ {displaystyle nrightarrow infty }. Os dois estimadores também são assintoticamente normais:
- n(σ σ ^ ^ 2- Sim. - Sim. σ σ 2)≃ ≃ n(S2- Sim. - Sim. σ σ 2)→DN(0,2σ σ 4).(em inglês) }}^{2}-sigma ^{2})simeq {sqrt {n}}(s^{2}-sigma ^{2}),{xrightarrow {d}},{mathcal {N}}(0,2sigma ^{4}). ?
Em particular, ambos os estimadores são assintoticamente eficientes para σ σ 2{displaystyle sigma ^{2}}.
Intervalos de confiança
Por teorema de Cochran, para distribuições normais a média da amostra μ μ ^ ^ {displaystyle textstyle {hat {mu}) e a variância da amostra S2 são independentes, o que significa que não pode haver ganho em considerar sua distribuição conjunta. Há também um teorema converso: se em uma amostra a média da amostra e a variância da amostra são independentes, então a amostra deve ter vindo da distribuição normal. A independência entre μ μ ^ ^ {displaystyle textstyle {hat {mu}) e S pode ser empregado para construir o chamado t-estatística:
- )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =μ μ ^ ^ - Sim. - Sim. μ μ S/n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =x? ? - Sim. - Sim. μ μ 1n(n- Sim. - Sim. 1)Gerenciamento Gerenciamento (xEu...- Sim. - Sim. x? ? )2∼ ∼ )n- Sim. - Sim. 1Não. }}-mu ? {n}}}=**** {{overline {x}}-mu }{sqrt {{frac {1}{n(n-1)}}sum (x_{i}-{overline {x}}^{2}}sim t_{n-1}}
Esta quantidade t tem a distribuição t de Student com (n − 1) graus de liberdade, e é uma estatística auxiliar (independente do valor dos parâmetros). A inversão da distribuição desta estatística t nos permitirá construir o intervalo de confiança para μ; da mesma forma, inverter a distribuição χ2 da estatística s2 nos dará o intervalo de confiança para σ2:
- μ μ ∈ ∈ Não.μ μ ^ ^ - Sim. - Sim. )n- Sim. - Sim. 1,1- Sim. - Sim. α α /21nS,μ μ ^ ^ +)n- Sim. - Sim. 1,1- Sim. - Sim. α α /21nS],{displaystyle mu in left[{hat] }}-t_{n-1,1-alpha /2}{frac {1}{sqrt {n}}}s,{hat {mu }}+t_{n-1,1-alpha /2}{frac {1}{sqrt {n}}}sright],}
- σ σ 2∈ ∈ Não.(n- Sim. - Sim. 1)S2χ χ n- Sim. - Sim. 1,1- Sim. - Sim. α α /22,(n- Sim. - Sim. 1)S2χ χ n- Sim. - Sim. 1,α α /22],{displaystyle sigma ^{2}in left[{frac {(n-1)s^{2}}{chi _{n-1,1-alpha /2}^{2}}},{frac {(n-1)s^{2}}{chi _{n-1,alpha /2}^{2}}}right],}
onde tk,p e χ 2
k,p são os pésimo quantis de t- e χ2- distribuições respectivamente. Esses intervalos de confiança são do nível de confiança 1 − α, significando que os valores verdadeiros μ e σ2 ficam fora desses intervalos com probabilidade (ou nível de significância) α. Na prática, as pessoas geralmente consideram α = 5%, resultando em intervalos de confiança de 95%.
Fórmulas aproximadas podem ser derivadas das distribuições assintóticas de μ μ ^ ^ {displaystyle textstyle {hat {mu}) e S2:
- μ μ ∈ ∈ Não.μ μ ^ ^ - Sim. - Sim. |zangão.α α /2|1nS,μ μ ^ ^ +|zangão.α α /2|1nS],{displaystyle mu in left[{hat] }}-|z_{alpha /2}|{frac {1}{sqrt {n}}}s,{hat {mu }}+|z_{alpha /2}|{frac {1}{sqrt {n}}}sright,}
- σ σ 2∈ ∈ Não.S2- Sim. - Sim. |zangão.α α /2|2nS2,S2+|zangão.α α /2|2nS2],{displaystyle sigma ^{2}in left [s^{2}-|z_{alpha /2}|{frac {2} {n}}}s^{2},s^{2}+|z_{alpha /2}|{frac {sqrt {2}}{sqrt {n}}}s^{2}right],}
As fórmulas aproximadas tornam-se válidas para grandes valores de n e são mais convenientes para o cálculo manual, pois os quantis normais padrão zα/2 não dependem de n. Em particular, o valor mais popular de α = 5%, resulta em |z0,025| = 1,96.
Testes de normalidade
Testes de normalidade avaliam a probabilidade de que o conjunto de dados fornecido {x1,..., xn} vem de uma distribuição normal. Normalmente, a hipótese nula H0 é que as observações são distribuídas normalmente com média não especificada μ e variância σ2, versus a alternativa Ha de que a distribuição é arbitrária. Muitos testes (mais de 40) foram concebidos para este problema. Os mais proeminentes deles são descritos abaixo:
Gráficos diagnósticos são mais atraentes intuitivamente, mas ao mesmo tempo subjetivos, pois dependem do julgamento humano informal para aceitar ou rejeitar a hipótese nula.
- O gráfico Q-Q, também conhecido como gráfico de probabilidade normal ou plotagem rankit, é um enredo dos valores classificados dos dados definidos contra os valores esperados dos quantis correspondentes da distribuição normal padrão. Isto é, é um enredo de ponto da forma (Φ- Sim.(pk), x(k)), onde os pontos de plotagem pk são iguais a pkNão.k- Sim.α)n+ 1 − 2α) e α é uma constante de ajuste, que pode ser qualquer coisa entre 0 e 1. Se a hipótese nula for verdadeira, os pontos plotados devem aproximadamente estar em linha reta.
- plotagem P-P – semelhante ao gráfico Q-Q, mas usado muito menos frequentemente. Este método consiste em traçar os pontos (Φ(zangão.(k)), pk), onde zangão.(k)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(x(k)- Sim. - Sim. μ μ ^ ^ )/σ σ ^ ^ {displaystyle textstyle z_{(k)}=(x_{(k)}-{hat {mu }})/{hat {sigma). Para dados normalmente distribuídos este enredo deve estar em uma linha de 45 ° entre (0, 0) e (1, 1).
Testes de qualidade de ajuste:
Testes baseados em momentos:
- Teste K-quadrado de D'Agostino
- Teste de Jarque–Bera
- Teste de Shapiro-Wilk: Isso é baseado no fato de que a linha na trama Q-Q tem a inclinação σ. O teste compara a estimativa mínima de quadrados dessa inclinação com o valor da variância amostral, e rejeita a hipótese nula se essas duas quantidades diferem significativamente.
Testes baseados na função de distribuição empírica:
- Teste de Anderson–Darling
- Teste de Lilliefors (uma adaptação do teste de Kolmogorov–Smirnov)
Análise bayesiana da distribuição normal
A análise bayesiana de dados normalmente distribuídos é complicada pelas muitas possibilidades diferentes que podem ser consideradas:
- Ou a média, ou a variância, ou nenhum, pode ser considerada uma quantidade fixa.
- Quando a variância é desconhecida, a análise pode ser feita diretamente em termos de variância, ou em termos de precisão, o recíproco da variância. A razão para expressar as fórmulas em termos de precisão é que a análise da maioria dos casos é simplificada.
- Ambos os casos univariados e multivariados precisam ser considerados.
- As distribuições prévias conjugadas ou impróprias podem ser colocadas nas variáveis desconhecidas.
- Um conjunto adicional de casos ocorre na regressão linear bayesiana, onde no modelo básico os dados são normalmente distribuídos, e os antecedentes normais são colocados nos coeficientes de regressão. A análise resultante é semelhante aos casos básicos de dados distribuídos de forma idêntica independente.
As fórmulas para os casos de regressão não linear estão resumidas no artigo anterior conjugado.
Soma de duas quadráticas
Forma escalar
A fórmula auxiliar a seguir é útil para simplificar as equações de atualização posterior, que de outra forma se tornam bastante tediosas.
- um(x- Sim. - Sim. Sim.)2+b)(x- Sim. - Sim. zangão.)2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(um+b))(x- Sim. - Sim. umSim.+b)zangão.um+b))2+umb)um+b)(Sim.- Sim. - Sim. zangão.)2(x-y)^{2}+b(x-z)^{2}=(a+b)left(x-{frac {ay+bz}{a+b}}right)^{2}+{frac {ab}{a+b}}(y-z)^{2}}
Esta equação reescreve a soma de duas quadráticas em x expandindo os quadrados, agrupando os termos em x e completando o quadrado. Observe o seguinte sobre os fatores constantes complexos associados a alguns dos termos:
- O factor umSim.+b)zangão.um+b)Não. tem a forma de uma média ponderada de Sim. e zangão..
- umb)um+b)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =11um+1b)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(um- Sim. - Sim. 1+b)- Sim. - Sim. 1)- Sim. - Sim. 1.Não. - Não. Não. - Sim. {1}{b}}=(a^{-1}+b^{-1})^{-1}.} Isto mostra que este fator pode ser pensado como resultado de uma situação em que os recíprocos de quantidades um e b) adicionar diretamente, de modo a combinar um e b) eles mesmos, é necessário retribuir, adicionar e retribuir o resultado novamente para voltar para as unidades originais. Este é exatamente o tipo de operação realizada pela média harmônica, então não é surpreendente que umb)um+b)Não. Não. é uma metade da média harmônica de um e b).
Forma vetorial
Uma fórmula semelhante pode ser escrita para a soma de dois quadráticos vetoriais: Se x, Sim., zangão. são vetores de comprimento ke A e B são matrizes simétricas, invertíveis de tamanho k× × k{displaystyle ktimes k}, então
- (Sim.- Sim. - Sim. x)?A(Sim.- Sim. - Sim. x)+(x- Sim. - Sim. zangão.)?B(x- Sim. - Sim. zangão.)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(x- Sim. - Sim. c)?(A+B)(x- Sim. - Sim. c)+(Sim.- Sim. - Sim. zangão.)?(A- Sim. - Sim. 1+B- Sim. - Sim. 1)- Sim. - Sim. 1(Sim.- Sim. - Sim. zangão.)(mathbf {y} -mathbf {y} -mathbf {x})'mathbf {A} (mathbf {y} -mathbf {x})+(mathbf {x}) },,,,,,,,,, },,, },,,,,,,, },,,,,,,,,,,,,,,,,,,)
onde
- c= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(A+B)- Sim. - Sim. 1(ASim.+Bzangão.){displaystyle mathbf {c} =(mathbf {A} +mathbf {B})^{-1}(mathbf {A} mathbf {y} +mathbf {B} mathbf {z})}
Observe que a forma x′ A x é chamada de forma quadrática e é escalar:
- x?Ax= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...,JJumEu...JJxEu...xJJ{displaystyle mathbf {x}mathbf {A} mathbf {x} =sum _{i,j}a_{ij}x_{i}x_{j}}
Em outras palavras, resume todas as combinações possíveis de produtos de pares de elementos de x, com um coeficiente separado para cada um. Além disso, desde xEu...xJJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =xJJxEu...Não. x_{i}x_{j}=x_{j}x_{i}}, apenas a soma umEu...JJ+umJJEu...Não. a_{ij}+a_{ji}} assuntos para quaisquer elementos off-diagonal A, e não há perda de generalidade em assumir que A é simétrico. Além disso, se A é simétrico, então a forma x?ASim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Sim.?Ax.{displaystyle mathbf {x}mathbf {A} mathbf {y} =mathbf {y}mathbf {A} mathbf {x}}}}
Soma das diferenças da média
Outra fórmula útil é a seguinte:
Com variação conhecida
Para um conjunto de pontos de dados normalmente distribuídos i.i.d. X de tamanho n onde cada ponto individual x da seguinte forma: x∼ ∼ N(μ μ ,σ σ 2){displaystyle xsim {mathcal {N}}(musigma ^{2})} com variância conhecida σ2, a distribuição prévia conjugada também é normalmente distribuída.
Isso pode ser mostrado mais facilmente reescrevendo a variância como a precisão, ou seja, usando τ = 1/σ2. Então, se x∼ ∼ N(μ μ ,1/? ? ){displaystyle xsim {mathcal {N}}(mu1/tau)} e μ μ ∼ ∼ N(μ μ 0,1/? ? 0),{displaystyle mu sim {mathcal {N}}(mu _{0},1/tau _{0}),} procedemos da seguinte forma.
Primeiro, a função de verossimilhança é (usando a fórmula acima para a soma das diferenças da média):
- p(X∣ ∣ μ μ ,? ? )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n? ? 2D D exp (- Sim. - Sim. 12? ? (xEu...- Sim. - Sim. μ μ )2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(? ? 2D D )n/2exp (- Sim. - Sim. 12? ? Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n(xEu...- Sim. - Sim. μ μ )2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(? ? 2D D )n/2exp Não.- Sim. - Sim. 12? ? (Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n(xEu...- Sim. - Sim. x? ? )2+n(x? ? - Sim. - Sim. μ μ )2)].{displaystyle {begin{aligned}p(mathbf {X} mid mutau)&=prod _{i=1}^{n}{sqrt {frac {tau }{2pi }}}exp left(-{frac {1}{2}}tau (x_{i}-mu)^{2}rightright)\&=left({frac)^{n/2exp}\left(-{frac {1}{2}}
Depois, procedemos da seguinte forma:
- p(μ μ ∣ ∣ X)∝ ∝ p(X∣ ∣ μ μ )p(μ μ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(? ? 2D D )n/2exp Não.- Sim. - Sim. 12? ? (Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n(xEu...- Sim. - Sim. x? ? )2+n(x? ? - Sim. - Sim. μ μ )2)]? ? 02D D exp (- Sim. - Sim. 12? ? 0(μ μ - Sim. - Sim. μ μ 0)2)∝ ∝ exp (- Sim. - Sim. 12(? ? (Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n(xEu...- Sim. - Sim. x? ? )2+n(x? ? - Sim. - Sim. μ μ )2)+? ? 0(μ μ - Sim. - Sim. μ μ 0)2))∝ ∝ exp (- Sim. - Sim. 12(n? ? (x? ? - Sim. - Sim. μ μ )2+? ? 0(μ μ - Sim. - Sim. μ μ 0)2))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =exp (- Sim. - Sim. 12(n? ? +? ? 0)(μ μ - Sim. - Sim. n? ? x? ? +? ? 0μ μ 0n? ? +? ? 0)2+n? ? ? ? 0n? ? +? ? 0(x? ? - Sim. - Sim. μ μ 0)2)∝ ∝ exp (- Sim. - Sim. 12(n? ? +? ? 0)(μ μ - Sim. - Sim. n? ? x? ? +? ? 0μ μ 0n? ? +? ? 0)2)(em inglês) {displaystyle begin{aligned}p(mu mid mathbf {X})&propto p(mathbf {X} mid mu)p(mu)\muleft(left({frac {tau }{2pi ^{2right)^{n/2}exp left[-{frac {1}{2}}tau left(} }}}exp left(-{frac {1}{2}}tau _{0}(mu -mu _{0})^{2}right)&propto exp left(-{frac {1}{2}}left(tau left(sum) _{i=1}^{n}(x_{i}-{bar {x}}^{2}+n({bar {x}}-mu)^{2}right)+tau _{0}(mu _{0})^{2}right)right)\&propto expleft(-{frac {1}{2}}leftntau (em inglês) Não. {x}}+tau _{0}mu _{0}}{ntau +tau _{0}}}right)^{2}+{frac {ntau tau _{0}}{ntau +tau _{0}}}({bar {x}}-mu _{0})^{2}right)&propto exp left(-{frac {1}{2}}(ntau +tau _{0})left(mu -{dfrac (em inglês) Não. {x}}+tau _{0}mu _{0}}{ntau +tau _{0}}}right)^{2}right)end{aligned}}}
Na derivação acima, usamos a fórmula acima para a soma de dois quadráticos e eliminamos todos os fatores constantes que não envolvemμ. O resultado é o kernel de uma distribuição normal, com média n? ? x? ? +? ? 0μ μ 0n? ? +? ? 0(em inglês) (x}}+tau _{0}mu _{0}}{ntau +tau _{0}}}} e precisão n? ? +? ? 0{displaystyle ntau +tau _{0}}, i.e.
- p(μ μ ∣ ∣ X)∼ ∼ N(n? ? x? ? +? ? 0μ μ 0n? ? +? ? 0,1n? ? +? ? 0){displaystyle p(mu mid mathbf {X})sim {mathcal {N}}left({frac {ntau {bar {x}}+tau _{0}mu _{0}}{ntau +tau _{0}}},{frac {1}{ntau +tau _{0}}}right)}
Isso pode ser escrito como um conjunto de equações de atualização Bayesiana para os parâmetros posteriores em termos dos parâmetros anteriores:
- ? ? 0?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? 0+n? ? μ μ 0?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =n? ? x? ? +? ? 0μ μ 0n? ? +? ? 0x? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nGerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nxEu...{displaystyle {begin{aligned}tau _{0}'&=tau _{0}+ntau \[5pt]mu _{0}'&={frac {ntau Não. {x}}+tau _{0}mu _{0}}{ntau +tau _{0}}}\[5pt]{bar {x}}&={frac {1}{n}}sum _{i=1}^{n}x_{i}end{aligned}}}
Isto é, combinar n pontos de dados com precisão total Não. (ou equivalente, variação total de n/σ2) e média dos valores x? ? (x), obter uma nova precisão total simplesmente adicionando a precisão total dos dados à precisão total anterior, e formar uma nova média através de uma média de precisão, ou seja, uma média ponderada dos dados significa e a média anterior, cada uma ponderada pela precisão total associada. Isso faz sentido lógico se a precisão for pensada como indicando a certeza das observações: Na distribuição da média posterior, cada um dos componentes de entrada é ponderado pela sua certeza, e a certeza desta distribuição é a soma das certezas individuais. (Para a intuição disso, compare a expressão "o todo é (ou não é) maior do que a soma de suas partes". Além disso, considere que o conhecimento do posterior vem de uma combinação do conhecimento do anterior e da probabilidade, por isso faz sentido que estamos mais certos dele do que de qualquer um de seus componentes.)
A fórmula acima revela por que é mais conveniente fazer análises bayesianas de prioris conjugadas para a distribuição normal em termos de precisão. A precisão posterior é simplesmente a soma das precisões anteriores e de verossimilhança, e a média posterior é calculada por meio de uma média ponderada pela precisão, conforme descrito acima. As mesmas fórmulas podem ser escritas em termos de variância retribuindo todas as precisões, resultando em fórmulas mais feias
- σ σ 02?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nσ σ 2+1σ σ 02μ μ 0?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =nx? ? σ σ 2+μ μ 0σ σ 02nσ σ 2+1σ σ 02x? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nGerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nxEu...- Sim. _{0}^{2}}'&={frac {1}{{frac {n}{sigma ^{2}}}+{frac Não. _{0}^{2}}}\[5pt]mu _{0}'&={frac {{frac {n{bar {x}}}{sigma ^{2}}}+{frac _{0}} _{0}^{2}}{{frac Não. ^{2}}}+{frac Não. _{0}^{2}}}\[5pt]{bar {x}}&={frac {1}{n}}sum _{i=1}^{n}x_{i}end{aligned}}}
Com média conhecida
Para um conjunto de pontos de dados normalmente distribuídos i.i.d. X de tamanho n onde cada ponto individual x da seguinte forma: x∼ ∼ N(μ μ ,σ σ 2){displaystyle xsim {mathcal {N}}(musigma ^{2})} com μ média conhecida, o conjugado anterior da variância tem uma distribuição inversa do gamma ou uma distribuição escalada do chi-quadrado inverso. Os dois são equivalentes, exceto por ter diferentes parâmetros. Embora o gamma inverso seja mais comumente usado, usamos o qui-quadrado inverso escalado para o bem da conveniência. O anterior para σ2 é o seguinte:
- p(σ σ 2∣ ∣ Processo Processo 0,σ σ 02)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(σ σ 02Processo Processo 02)Processo Processo 0/2)) (Processo Processo 02)exp Não.- Sim. - Sim. Processo Processo 0σ σ 022σ σ 2](σ σ 2)1+Processo Processo 02∝ ∝ exp Não.- Sim. - Sim. Processo Processo 0σ σ 022σ σ 2](σ σ 2)1+Processo Processo 02{displaystyle p(sigma ^{2}mid nu _{0},sigma _{0}^{2})={frac {(sigma _{0}^{2}{frac _{0}}{2}})^{nu _{0}/2}} Gamma left({frac) _{0}}{2}}right)}}~{frac {exp left[{frac {-nu _{0}sigma _{0}^{2}}{2sigma ^{2}}}right]}{(sigma ^{2})^{1+{frac {nu _{0}}{2}}}propto frac {displaystyle left{{{{{\\\\\\\\\\\\\\\\ _{0}sigma _{0}^{2}}{2sigma ^{2}}}right]}{(sigma ^{2})^{1+{frac {nu _{0}}{2}}}}}}
A função de verossimilhança acima, escrita em termos de variância, é:
- p(X∣ ∣ μ μ ,σ σ 2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(12D D σ σ 2)n/2exp Não.- Sim. - Sim. 12σ σ 2Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n(xEu...- Sim. - Sim. μ μ )2]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(12D D σ σ 2)n/2exp Não.- Sim. - Sim. S2σ σ 2]{displaystyle {begin{aligned}p(mathbf {X} mid musigma ^{2})&=left({frac {1}{2pi sigma ^{2}}}right)^{n/2}exp left[-{frac {1}{2sigma ^{2}}}sum _{i=1}^{n}(x_{i}-mu)^{2}right]&=left({frac {1}{2pi sigma ^{2}}}right)^{n/2}exp left[-{frac {S}{2sigma ^{2}}}right]end{aligned}}}
onde
- S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n(xEu...- Sim. - Sim. μ μ )2.- Sim. _{i=1}^{n}(x_{i}-mu)^{2}.}
Então:
- p(σ σ 2∣ ∣ X)∝ ∝ p(X∣ ∣ σ σ 2)p(σ σ 2)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(12D D σ σ 2)n/2exp Não.- Sim. - Sim. S2σ σ 2](σ σ 02Processo Processo 02)Processo Processo 02)) (Processo Processo 02)exp Não.- Sim. - Sim. Processo Processo 0σ σ 022σ σ 2](σ σ 2)1+Processo Processo 02∝ ∝ (1σ σ 2)n/21(σ σ 2)1+Processo Processo 02exp Não.- Sim. - Sim. S2σ σ 2+- Sim. - Sim. Processo Processo 0σ σ 022σ σ 2]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1(σ σ 2)1+Processo Processo 0+n2exp Não.- Sim. - Sim. Processo Processo 0σ σ 02+S2σ σ 2]{displaystyle {begin{aligned}p(sigma ^{2}mid mathbf {X})&propto p(mathbf {X} mid sigma ^{2})p(sigma ^{2})&=left({frac {1}{2pi sigma ^{2}}}right)^{n/2}exp left[-{frac {S}{2sigma ^{2}}}right]{frac {(sigma _{0}^{2}{frac {nu _{0}}{2}})^{frac {nu _{0}}{2}}}{Gamma left({frac _{0}}{2}}right)}}~{frac {exp left[{frac {-nu _{0}sigma _{0}^{2}}{2sigma ^{2}}}right]}{(sigma ^{2})^{1+{frac {nu _{0}}{2}}}}}\&propto left({frac {1}{sigma ^{2}}}right)^{n/2}{frac {1}{(sigma ^{2})^{1+{frac {nu _{0}}{2}}}}}exp left[-{frac Não. ^{2}}}+{frac {-nu _{0}sigma _{0}^{2}}{2sigma ^{2}}}right]&={frac {1}{(sigma ^{2})^{1+{frac _{0}+n}{2}}}}}exp left[-{frac Não. _{0}sigma _{0}^{2}+S}{2sigma ^{2}}}right]end{aligned}}}
A descrição acima também é uma distribuição qui-quadrada inversa em escala em que
- Processo Processo 0?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Processo Processo 0+nProcesso Processo 0?σ σ 02?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Processo Processo 0σ σ 02+Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n(xEu...- Sim. - Sim. μ μ )2{displaystyle {begin{aligned}nu _{0}'&=nu _{0}+n\nu _{0} _{0}^{2}}'&=nu _{0}sigma _{0}^{2}+sum _{i=1}^{n}(x_{i}-mu)^{2}end{aligned}}}
ou equivalente
- Processo Processo 0?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Processo Processo 0+nσ σ 02?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Processo Processo 0σ σ 02+Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n(xEu...- Sim. - Sim. μ μ )2Processo Processo 0+n{displaystyle {begin{aligned}nu _{0}'&=nu _{0}+n\{sigma _{0}^{2}} &={frac _{0}sigma _{0}^{2}+sum _{i=1}^{n}(x_{i}-mu)^{2}}{nu _{0}+n}}end{aligned}}}
Reparametrizando em termos de uma distribuição gama inversa, o resultado é:
- α α ?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =α α +n2β β ?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =β β +Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n(xEu...- Sim. - Sim. μ μ )22{displaystyle {begin{aligned}alpha’&=alpha +{frac {n}{2}}\beta '&=beta +{frac _{i=1}^{n}(x_{i}-mu)^{2}}{2}}end{aligned}}}
Com média desconhecida e variância desconhecida
Para um conjunto de pontos de dados normalmente distribuídos i.i.d. X de tamanho n onde cada ponto individual x da seguinte forma: x∼ ∼ N(μ μ ,σ σ 2){displaystyle xsim {mathcal {N}}(musigma ^{2})} com média desconhecida μ e variação desconhecida σ2, um conjugado (multivariado) antes é colocado sobre a média e variância, consistindo de uma distribuição normal-inverso-gama. Logicamente, isso se origina da seguinte forma:
- Da análise do caso com variância desconhecida média, mas conhecida, vemos que as equações de atualização envolvem estatísticas suficientes computadas a partir dos dados que consistem na média dos pontos de dados e da variância total dos pontos de dados, computados por sua vez da variância conhecida dividida pelo número de pontos de dados.
- Da análise do caso com variância desconhecida, mas média conhecida, vemos que as equações de atualização envolvem estatísticas suficientes sobre os dados que consistem no número de pontos de dados e soma de desvios quadrados.
- Tenha em mente que os valores de atualização posterior servem como a distribuição prévia quando novos dados são tratados. Assim, devemos logicamente pensar em nossos antecedentes em termos de estatísticas suficientes descritas, com as mesmas semânticas mantidas em mente tanto quanto possível.
- Para lidar com o caso em que ambas as médias e variância são desconhecidas, poderíamos colocar antecedentes independentes sobre a média e variância, com estimativas fixas da média, variância total, número de pontos de dados usados para calcular a variância anterior e soma de desvios quadrados. Note, porém, que na realidade, a variância total da média depende da variância desconhecida, e a soma de desvios quadrados que entra na variância anterior (parece) depende da média desconhecida. Na prática, a última dependência é relativamente pouco importante: mudar a média real muda os pontos gerados por uma quantidade igual, e em média os desvios quadrados permanecerão os mesmos. Este não é o caso, no entanto, com a variação total da média: À medida que a variância desconhecida aumenta, a variância total da média aumentará proporcionalmente, e gostaríamos de capturar essa dependência.
- Isso sugere que criamos um condição prévia da média na variância desconhecida, com um hiperparâmetro especificando a média das pseudo-observações associadas ao anterior, e outro parâmetro especificando o número de pseudo-observações. Este número serve como parâmetro de escala na variância, tornando possível controlar a variância geral da média em relação ao parâmetro de variância real. O anterior para a variância também tem dois hiperparametros, um especificando a soma de desvios quadrados das pseudo-observações associadas ao anterior, e outro especificando mais uma vez o número de pseudo-observações. Note que cada um dos antecedentes tem um hiperparâmetro especificando o número de pseudo-observações, e em cada caso isso controla a variância relativa daquele anterior. Estes são dados como dois hiperparâmetros separados para que a variância (aka a confiança) dos dois antecedentes possa ser controlada separadamente.
- Isso leva imediatamente à distribuição normal-inverso-gamma, que é o produto das duas distribuições acabadas de definir, com priores conjugados usados (uma distribuição de gama inversa sobre a variância, e uma distribuição normal sobre a média, condicional na variância) e com os mesmos quatro parâmetros definidos.
Os priores são normalmente definidos da seguinte forma:
- p(μ μ ∣ ∣ σ σ 2;μ μ 0,n0)∼ ∼ N(μ μ 0,σ σ 2/n0)p(σ σ 2;Processo Processo 0,σ σ 02)∼ ∼ Eu...χ χ 2(Processo Processo 0,σ σ 02)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...G(Processo Processo 0/2,Processo Processo 0σ σ 02/2){displaystyle {begin{aligned}p(mu mid sigma ^{2};mu _{0},n_{0})&sim {mathcal {N}}(mu _{0},sigma ^{2}/n_{0})p(sigma ^{2};nu _{0},sigma _{0}^{2})&sim Ichi ^{2}(nu _{0},sigma _{0}^{2})=IG(nu _{0}/2,nu _{0}sigma _{0}^{2}/2)end{aligned}}}
As equações de atualização podem ser derivadas e têm a seguinte aparência:
- x? ? = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nGerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nxEu...μ μ 0?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =n0μ μ 0+nx? ? n0+nn0?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =n0+nProcesso Processo 0?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Processo Processo 0+nProcesso Processo 0?σ σ 02?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Processo Processo 0σ σ 02+Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1n(xEu...- Sim. - Sim. x? ? )2+n0nn0+n(μ μ 0- Sim. - Sim. x? ? )2- Sim. {x}}&={frac {1}{n}}sum _{i=1}^{n}x_{i}\mu _{0}'&={frac {n_{0}mu _{0}+n{bar {x}}}{n_{0}+n}}\n_{0}'&=n_{0}+n\nu _{0}'&=nu _{0}+n\nu _{0} _{0}^{2}}'&=nu _{0}sigma _{0}^{2}+sum _{i=1}^{n}(x_{i}-{bar {x}}^{2}+{frac {n_{0}n}{n_{0}+n}}(mu) _{0}-{bar {x}}^{2}end{aligned}}}
Os respectivos números de pseudo-observações adicionam-lhes o número de observações reais. O novo hiperparâmetro médio é mais uma vez uma média ponderada, desta vez ponderada pelo número relativo de observações. Finalmente, a atualização para Processo Processo 0?σ σ 02?{displaystyle nu _{0}'{sigma _{0}^{2}}}}} é semelhante ao caso com média conhecida, mas neste caso a soma de desvios quadrados é tomada com relação aos dados observados significam em vez da verdadeira média, e como resultado um novo "termo de interação" precisa ser adicionado para cuidar da fonte de erro adicional decorrente do desvio entre prévio e média de dados.
The prior distributions are
- p ( μ ∣ σ 2 ; μ 0 , n 0 ) ∼ N ( μ 0 , σ 2 / n 0 ) = 1 2 π σ 2 n 0 exp ( − n 0 2 σ 2 ( μ − μ 0 ) 2 ) ∝ ( σ 2 ) − 1 / 2 exp ( − n 0 2 σ 2 ( μ − μ 0 ) 2 ) p ( σ 2 ; ν 0 , σ 0 2 ) ∼ I χ 2 ( ν 0 , σ 0 2 ) = I G ( ν 0 / 2 , ν 0 σ 0 2 / 2 ) = ( σ 0 2 ν 0 / 2 ) ν 0 / 2 Γ ( ν 0 / 2 ) exp [ − ν 0 σ 0 2 2 σ 2 ] ( σ 2 ) 1 + ν 0 / 2 ∝ ( σ 2 ) − ( 1 + ν 0 / 2 ) exp [ − ν 0 σ 0 2 2 σ 2 ] . {displaystyle {begin{aligned}p(mu mid sigma ^{2};mu _{0},n_{0})&sim {mathcal {N}}(mu _{0},sigma ^{2}/n_{0})={frac {1}{sqrt {2pi {frac {sigma ^{2}}{n_{0}}}}}}exp left(-{frac {n_{0}}{2sigma ^{2}}}(mu -mu _{0})^{2}right)\&propto (sigma ^{2})^{-1/2}exp left(-{frac {n_{0}}{2sigma ^{2}}}(mu -mu _{0})^{2}right)\p(sigma ^{2};nu _{0},sigma _{0}^{2})&sim Ichi ^{2}(nu _{0},sigma _{0}^{2})=IG(nu _{0}/2,nu _{0}sigma _{0}^{2}/2)\&={frac {(sigma _{0}^{2}nu _{0}/2)^{nu _{0}/2}}{Gamma (nu _{0}/2)}}~{frac {exp left[{frac {-nu _{0}sigma _{0}^{2}}{2sigma ^{2}}}right]}{(sigma ^{2})^{1+nu _{0}/2}}}\&propto {(sigma ^{2})^{-(1+nu _{0}/2)}}exp left[{frac {-nu _{0}sigma _{0}^{2}}{2sigma ^{2}}}right].end{aligned}}}
Therefore, the joint prior is
- p ( μ , σ 2 ; μ 0 , n 0 , ν 0 , σ 0 2 ) = p ( μ ∣ σ 2 ; μ 0 , n 0 ) p ( σ 2 ; ν 0 , σ 0 2 ) ∝ ( σ 2 ) − ( ν 0 + 3 ) / 2 exp [ − 1 2 σ 2 ( ν 0 σ 0 2 + n 0 ( μ − μ 0 ) 2 ) ] . {displaystyle {begin{aligned}p(musigma ^{2};mu _{0},n_{0},nu _{0},sigma _{0}^{2})&=p(mu mid sigma ^{2};mu _{0},n_{0}),p(sigma ^{2};nu _{0},sigma _{0}^{2})\&propto (sigma ^{2})^{-(nu _{0}+3)/2}exp left[-{frac {1}{2sigma ^{2}}}left(nu _{0}sigma _{0}^{2}+n_{0}(mu -mu _{0})^{2}right)right].end{aligned}}}
The likelihood function from the section above with known variance is:
- p ( X ∣ μ , σ 2 ) = ( 1 2 π σ 2 ) n / 2 exp [ − 1 2 σ 2 ( ∑ i = 1 n ( x i − μ ) 2 ) ] {displaystyle {begin{aligned}p(mathbf {X} mid musigma ^{2})&=left({frac {1}{2pi sigma ^{2}}}right)^{n/2}exp left[-{frac {1}{2sigma ^{2}}}left(sum _{i=1}^{n}(x_{i}-mu)^{2}right)right]end{aligned}}}
Writing it in terms of variance rather than precision, we get:
- p ( X ∣ μ , σ 2 ) = ( 1 2 π σ 2 ) n / 2 exp [ − 1 2 σ 2 ( ∑ i = 1 n ( x i − x ¯ ) 2 + n ( x ¯ − μ ) 2 ) ] ∝ σ 2 − n / 2 exp [ − 1 2 σ 2 ( S + n ( x ¯ − μ ) 2 ) ] {displaystyle {begin{aligned}p(mathbf {X} mid musigma ^{2})&=left({frac {1}{2pi sigma ^{2}}}right)^{n/2}exp left[-{frac {1}{2sigma ^{2}}}left(sum _{i=1}^{n}(x_{i}-{bar {x}})^{2}+n({bar {x}}-mu)^{2}right)right]\&propto {sigma ^{2}}^{-n/2}exp left[-{frac {1}{2sigma ^{2}}}left(S+n({bar {x}}-mu)^{2}right)right]end{aligned}}}
where S = ∑ i = 1 n ( x i − x ¯ ) 2 . {textstyle S=sum _{i=1}^{n}(x_{i}-{bar {x}})^{2}.}
Therefore, the posterior is (dropping the hyperparameters as conditioning factors):
- p ( μ , σ 2 ∣ X ) ∝ p ( μ , σ 2 ) p ( X ∣ μ , σ 2 ) ∝ ( σ 2 ) − ( ν 0 + 3 ) / 2 exp [ − 1 2 σ 2 ( ν 0 σ 0 2 + n 0 ( μ − μ 0 ) 2 ) ] σ 2 − n / 2 exp [ − 1 2 σ 2 ( S + n ( x ¯ − μ ) 2 ) ] = ( σ 2 ) − ( ν 0 + n + 3 ) / 2 exp [ − 1 2 σ 2 ( ν 0 σ 0 2 + S + n 0 ( μ − μ 0 ) 2 + n ( x ¯ − μ ) 2 ) ] = ( σ 2 ) − ( ν 0 + n + 3 ) / 2 exp [ − 1 2 σ 2 ( ν 0 σ 0 2 + S + n 0 n n 0 + n ( μ 0 − x ¯ ) 2 + ( n 0 + n ) ( μ − n 0 μ 0 + n x ¯ n 0 + n ) 2 ) ] ∝ ( σ 2 ) − 1 / 2 exp [ − n 0 + n 2 σ 2 ( μ − n 0 μ 0 + n x ¯ n 0 + n ) 2 ] × ( σ 2 ) − ( ν 0 / 2 + n / 2 + 1 ) exp [ − 1 2 σ 2 ( ν 0 σ 0 2 + S + n 0 n n 0 + n ( μ 0 − x ¯ ) 2 ) ] = N μ ∣ σ 2 ( n 0 μ 0 + n x ¯ n 0 + n , σ 2 n 0 + n ) ⋅ I G σ 2 ( 1 2 ( ν 0 + n ) , 1 2 ( ν 0 σ 0 2 + S + n 0 n n 0 + n ( μ 0 − x ¯ ) 2 ) ) . {displaystyle {begin{aligned}p(musigma ^{2}mid mathbf {X})&propto p(musigma ^{2}),p(mathbf {X} mid musigma ^{2})\&propto (sigma ^{2})^{-(nu _{0}+3)/2}exp left[-{frac {1}{2sigma ^{2}}}left(nu _{0}sigma _{0}^{2}+n_{0}(mu -mu _{0})^{2}right)right]{sigma ^{2}}^{-n/2}exp left[-{frac {1}{2sigma ^{2}}}left(S+n({bar {x}}-mu)^{2}right)right]\&=(sigma ^{2})^{-(nu _{0}+n+3)/2}exp left[-{frac {1}{2sigma ^{2}}}left(nu _{0}sigma _{0}^{2}+S+n_{0}(mu -mu _{0})^{2}+n({bar {x}}-mu)^{2}right)right]\&=(sigma ^{2})^{-(nu _{0}+n+3)/2}exp left[-{frac {1}{2sigma ^{2}}}left(nu _{0}sigma _{0}^{2}+S+{frac {n_{0}n}{n_{0}+n}}(mu _{0}-{bar {x}})^{2}+(n_{0}+n)left(mu -{frac {n_{0}mu _{0}+n{bar {x}}}{n_{0}+n}}right)^{2}right)right]\&propto (sigma ^{2})^{-1/2}exp left[-{frac {n_{0}+n}{2sigma ^{2}}}left(mu -{frac {n_{0}mu _{0}+n{bar {x}}}{n_{0}+n}}right)^{2}right]\&quad times (sigma ^{2})^{-(nu _{0}/2+n/2+1)}exp left[-{frac {1}{2sigma ^{2}}}left(nu _{0}sigma _{0}^{2}+S+{frac {n_{0}n}{n_{0}+n}}(mu _{0}-{bar {x}})^{2}right)right]\&={mathcal {N}}_{mu mid sigma ^{2}}left({frac {n_{0}mu _{0}+n{bar {x}}}{n_{0}+n}},{frac {sigma ^{2}}{n_{0}+n}}right)cdot {rm {IG}}_{sigma ^{2}}left({frac {1}{2}}(nu _{0}+n),{frac {1}{2}}left(nu _{0}sigma _{0}^{2}+S+{frac {n_{0}n}{n_{0}+n}}(mu _{0}-{bar {x}})^{2}right)right).end{aligned}}}
In other words, the posterior distribution has the form of a product of a normal distribution over p(μ | σ2) times an inverse gamma distribution over p(σ2), with parameters that are the same as the update equations above.
Ocorrência e aplicações
A ocorrência de distribuição normal em problemas práticos pode ser vagamente classificada em quatro categorias:
- distribuições exatamente normais;
- Aproximadamente leis normais, por exemplo, quando tal aproximação é justificada pelo teorema do limite central; e
- Distribuições modeladas como normais - a distribuição normal é a distribuição com entropia máxima para uma determinada média e variância.
- Problemas de regressão – a distribuição normal que está sendo encontrada após efeitos sistemáticos foi modelada suficientemente bem.
Exata normalidade
Certas quantidades em física são distribuídas normalmente, como foi demonstrado pela primeira vez por James Clerk Maxwell. Exemplos de tais quantidades são:
- Função de densidade de probabilidade de um estado de terra em um oscilador harmônico quântico.
- A posição de uma partícula que experimenta difusão. Se inicialmente a partícula está localizada em um ponto específico (que é sua distribuição de probabilidade é a função delta de Dirac), então após o tempo ) sua localização é descrita por uma distribuição normal com variância ), que satisfaz a equação de difusão∂ ∂ ∂ ∂ )f(x,))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12∂ ∂ 2∂ ∂ x2f(x,)){displaystyle {frac {partial }{partial t}}f(x,t)={frac {1}{2}}{frac {partial ^{2}}{partial x^{2}}}f(x,t)}. Se a localização inicial for dada por uma determinada função de densidade g(x)(x)}, então a densidade no tempo ) é a convolução de g e o PDF normal.
Normalidade aproximada
DistribuiçõesAproximadamente normais ocorrem em muitas situações, conforme explicado pelo teorema do limite central. Quando o resultado é produzido por muitos pequenos efeitos agindo aditivamente e independentemente, sua distribuição será próxima do normal. A aproximação normal não será válida se os efeitos atuarem de forma multiplicativa (em vez de aditiva), ou se houver uma única influência externa que tenha uma magnitude consideravelmente maior que o restante dos efeitos.
- Na contagem de problemas, onde o teorema do limite central inclui uma aproximação discreta ao contínuo e onde estão envolvidas distribuições infinitamente divisíveis e decomponíveis, tais como
- Variáveis aleatórias binomiais, associadas a variáveis de resposta binária;
- Variáveis aleatórias de Poisson, associadas a eventos raros;
- A radiação térmica tem uma distribuição Bose-Einstein em escalas de tempo muito curtas, e uma distribuição normal em escalas de tempo mais longas devido ao teorema do limite central.
Normalidade assumida
Eu só posso reconhecer a ocorrência da curva normal – a curva Laplaciana de erros – como um fenômeno muito anormal. É aproximadamente aproximado em certas distribuições; por isso, e por causa de sua bela simplicidade, podemos, talvez, usá-lo como uma primeira aproximação, particularmente em investigações teóricas.
—Pearson (1901)
Existem métodos estatísticos para testar empiricamente essa suposição; consulte a seção de testes de normalidade acima.
- Em biologia, o - Não. de várias variáveis tendem a ter uma distribuição normal, ou seja, eles tendem a ter uma distribuição log-normal (após a separação em subpopulações masculinas/femininas), com exemplos incluindo:
- Medidas de tamanho do tecido vivo (comprimento, altura, área da pele, peso);
- O comprimento de inerte apêndices (hair, garras, unhas, dentes) de espécimes biológicos, na direção do crescimento; presumivelmente a espessura da casca da árvore também cai sob esta categoria;
- Determinadas medidas fisiológicas, como a pressão arterial de humanos adultos.
- Em finanças, em particular o modelo Black-Scholes, mudanças no - Não. de taxas de câmbio, índices de preços e índices de mercado de ações são assumidos normais (estas variáveis comportam-se como interesse composto, não como interesse simples, e assim são multiplicativas). Alguns matemáticos como Benoit Mandelbrot argumentaram que as distribuições de log-Levy, que possuem caudas pesadas, seriam um modelo mais apropriado, em particular para a análise de falhas no mercado de ações. O uso da suposição de distribuição normal que ocorre em modelos financeiros também foi criticado por Nassim Nicholas Taleb em suas obras.
- Erros de medição em experimentos físicos são frequentemente modelados por uma distribuição normal. Este uso de uma distribuição normal não implica que se está assumindo que os erros de medição são normalmente distribuídos, em vez de usar a distribuição normal produz as previsões mais conservadoras possíveis dado apenas conhecimento sobre a média e variância dos erros.
- Em testes padronizados, os resultados podem ser feitos para ter uma distribuição normal, selecionando o número e a dificuldade de perguntas (como no teste de QI) ou transformando os resultados dos testes crus em escores de "saída", ajustando-os à distribuição normal. Por exemplo, a gama tradicional do SAT de 200 a 800 é baseada em uma distribuição normal com uma média de 500 e um desvio padrão de 100.
- Muitos escores são derivados da distribuição normal, incluindo fileiras percentis ("percentiles" ou "quantiles"), equivalentes de curva normal, stanines, z-scores e T-scores. Além disso, alguns procedimentos estatísticos comportamentais assumem que os escores são normalmente distribuídos; por exemplo, testes t e ANOVAs. A classificação da curva de Bell atribui notas relativas com base em uma distribuição normal de escores.
- Em hidrologia, a distribuição de descarga ou chuva de rio de longa duração, por exemplo, totais mensais e anuais, é frequentemente considerada praticamente normal de acordo com o teorema do limite central. A imagem azul, feita com a CumFreq, ilustra um exemplo de adequar a distribuição normal às chuvas de outubro classificadas mostrando o cinto de confiança de 90% com base na distribuição binomial. Os dados de precipitação são representados por posições de plotagem como parte da análise de frequência cumulativa.
Problemas metodológicos e revisão por pares
John Ioannidis argumenta que usar desvios padrão normalmente distribuídos como padrões para validar descobertas de pesquisas deixa previsões falsificáveis sobre fenômenos que não são normalmente distribuídos sem serem testadas. Isso inclui, por exemplo, fenômenos que só aparecem quando todas as condições necessárias estão presentes e um não pode ser substituído por outro de maneira semelhante à adição e fenômenos que não são distribuídos aleatoriamente. Ioannidis argumenta que a validação centrada no desvio padrão dá uma falsa aparência de validade a hipóteses e teorias em que algumas, mas não todas as previsões falsificáveis são normalmente distribuídas, uma vez que a porção de previsões falsificáveis contra as quais há evidências pode e, em alguns casos, estão no anormalmente partes distribuídas do intervalo de previsões falsificáveis, bem como descartar hipóteses sem base para as quais nenhuma das previsões falsificáveis são normalmente distribuídas como se fossem infalsificáveis, quando na verdade fazem previsões falsificáveis. É argumentado por Ioannidis que muitos casos de teorias mutuamente exclusivas sendo aceitas como "validadas" por periódicos de pesquisa são causados pelo fracasso dos periódicos em aceitar falsificações empíricas de previsões não normalmente distribuídas, e não porque teorias mutuamente exclusivas são verdadeiras, o que não pode ser, embora duas teorias mutuamente exclusivas possam estar erradas e uma terceira correta.
Métodos computacionais
Gerando valores de distribuição normal

Em simulações de computador, especialmente em aplicações do método de Monte-Carlo, muitas vezes é desejável gerar valores que são normalmente distribuídos. Todos os algoritmos listados abaixo geram os desvios normais padrão, pois a N(μ, σ 2) pode ser gerado como X = μ + σZ, onde Z é normal padrão. Todos esses algoritmos contam com a disponibilidade de um gerador de números aleatórios U capaz de produzir variáveis aleatórias uniformes.
- O método mais simples é baseado na propriedade de transformação integral de probabilidade: se U é distribuído uniformemente em (0,1), então Φ- Sim.(U) terá a distribuição normal padrão. A desvantagem deste método é que ele depende do cálculo da função de probit Φ- Sim., que não pode ser feito de forma analítica. Alguns métodos aproximados são descritos em Hart (1968) e no artigo erf. Wichura dá um algoritmo rápido para computar esta função a 16 lugares decimais, que é usado por R para computar variações aleatórias da distribuição normal.
- Uma abordagem aproximada fácil de programa que depende do teorema do limite central é a seguinte: gerar 12 uniformes U(0,1) desvios, adicioná-los todos, e subtrair 6 – a variável aleatória resultante terá aproximadamente distribuição normal padrão. Na verdade, a distribuição será Irwin-Hall, que é uma aproximação polinomial de 11a ordem de 12 seções à distribuição normal. Este desvio aleatório terá um intervalo limitado de (−6, 6). Note que em uma distribuição normal verdadeira, apenas 0,00034% de todas as amostras cairão fora ±6σ.
- O método Box-Muller usa dois números aleatórios independentes U e V distribuído uniformemente em (0,1). Em seguida, as duas variáveis aleatórias X e Y ambos terão a distribuição normal padrão, e será independente. Esta formulação surge porque para um vetor aleatório normal bivariado (X, Y) a norma quadrada X2 + Y2 terá a distribuição qui-quadrado com dois graus de liberdade, que é uma variável aleatória exponencial facilmente gerada correspondente à quantidade −2ln(U) nestas equações; e o ângulo é distribuído uniformemente ao redor do círculo, escolhido pela variável aleatória V.X= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 2I Ue (2D D V),Y= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 2I Upecado (2D D V).{displaystyle X={sqrt {-2ln U}},cos(2pi V),qquad Y={sqrt {-2ln U}},sin(2pi V).}
- O método polar Marsaglia é uma modificação do método Box-Muller que não requer computação das funções sine e cosine. Neste método, U e V são extraídos da distribuição uniforme (−1,1) e, em seguida, S = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = U2 + V2 é computado. Se S é maior ou igual a 1, então o método começa mais, caso contrário as duas quantidades são devolvidos. Outra vez, X e Y são variáveis aleatórias normais independentes.X= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =U- Sim. - Sim. 2I SS,Y= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =V- Sim. - Sim. 2I SS- Sim. (-2 S}{S}}},qquad Y=V{sqrt (em inglês) - Sim.
- O método Ratio é um método de rejeição. O algoritmo segue:
- Gerar dois desvios uniformes independentes U e V;
- Compute X = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = √8/e (V - 0,5)/U;
- Opcional: se X2 ≤ 5 − 4e1/4U então aceitar X e terminar algoritmo;
- Opcional: se X2 ≥ 4e-1.35/U + 1.4 então rejeitar X e recomeçar da etapa 1;
- Se X2 ≤ −4 lnU então aceitar X, de outra forma começar sobre o algoritmo.
- As duas etapas opcionais permitem a avaliação do logaritmo na última etapa a ser evitada na maioria dos casos. Estas etapas podem ser muito melhoradas para que o logaritmo seja raramente avaliado.
- O algoritmo de ziggurat é mais rápido do que a transformada Box-Muller e ainda exato. Em cerca de 97% de todos os casos usa apenas dois números aleatórios, um inteiro aleatório e um uniforme aleatório, uma multiplicação e um teste se. Apenas em 3% dos casos, onde a combinação desses dois cai fora do "núcleo do ziggurat" (uma espécie de amostragem de rejeição usando logaritmos), fazer exponenciais e números aleatórios mais uniformes têm de ser empregados.
- A aritmética do inteiro pode ser usada para amostrar da distribuição normal padrão. Este método é exato no sentido de que satisfaz as condições de aproximação ideal; ou seja, é equivalente a amostragem de um número real da distribuição normal padrão e arredondando isso para o número de ponto flutuante representável mais próximo.
- Há também alguma investigação sobre a conexão entre a rápida transformação de Hadamard e a distribuição normal, uma vez que a transformação emprega apenas adição e subtração e pelo teorema do limite central números aleatórios de quase qualquer distribuição serão transformados na distribuição normal. A este respeito, uma série de transformações Hadamard pode ser combinada com permutações aleatórias para transformar conjuntos de dados arbitrários em dados normalmente distribuídos.
Aproximações numéricas para o CDF normal e a função quantílica normal
O CDF normal padrão é amplamente utilizado em computação científica e estatística.
Os valores Φ(x) podem ser aproximados com muita precisão por uma variedade de métodos, como integração numérica, série de Taylor, série assintótica e frações contínuas. Diferentes aproximações são usadas dependendo do nível de precisão desejado.
- Zelen & Severo (1964) dão a aproximação a Φ(x) para x > 0 com o erro absoluto |ε(x)< 7.5.10-8 (Algorithm 26.2.17): Onde? φ(x) é o PDF normal padrão, e b)0 = 0,2316419, b)1 = 0.319381530, b)2 = −0.356563782, b)3 = 1.781477937, b)4 = −1.821255978, b)5 = 1.330274429.Φ Φ (x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1- Sim. - Sim. φ φ (x)(b)1)+b)2)2+b)3)3+b)4)4+b)5)5)+ε ε (x),)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =11+b)0x,Não. Phi (x)=1-varphi (x)left (b_{1}t+b_{2}t^{2}+b_{3}t^{3}+b_{4}t^{4}+b_{5}t^{5}right)+varepsilon (x),qquad t={frac {1}{1+b_{0}x}},}
- Hart (1968) lista algumas dezenas de aproximações – por meio de funções racionais, com ou sem exponenciais – para os erfc() função. Seus algoritmos variam no grau de complexidade e na precisão resultante, com máxima precisão absoluta de 24 dígitos. Um algoritmo de West (2009) combina o algoritmo de Hart 5666 com uma aproximação contínua da fração na cauda para fornecer um algoritmo de computação rápida com uma precisão de 16 dígitos.
- Cody (1969) depois de evocar a solução Hart68 não é adequada para erf, dá uma solução para ambos erf e erfc, com erro relativo maximal ligado, através da aproximação Rational Chebyshev.
- Marsaglia (2004) sugeriu um algoritmo simples baseado na expansão da série Taylor para cálculo Φ(x) com precisão arbitrária. A desvantagem deste algoritmo é comparativamente tempo de cálculo lento (por exemplo, leva mais de 300 iterações para calcular a função com 16 dígitos de precisão quando x = 10).Φ Φ (x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12+φ φ (x)(x+x33+x53)) 5+x73)) 5)) 7+x93)) 5)) 7)) 9+⋯ ⋯ )Não. Phi (x)={frac {1}{2}}+varphi (x)left(x+{frac {x^{3}}{3}}+{frac {x^{5}}{3cdot 5}}+{frac {x^{7}}{3cdot 5cdot 7}}+{frac {x^{9}}{3cdot 5cdot 7cdot 9}}+cdots right)}
- A Biblioteca Científica GNU calcula valores do CDF normal padrão usando algoritmos e aproximações de Hart com polinômios de Chebyshev.
Shore (1982) introduziu aproximações simples que podem ser incorporadas em modelos de otimização estocástica de engenharia e pesquisa operacional, como engenharia de confiabilidade e análise de estoque. Denotando p = Φ(z), a aproximação mais simples para a função quantil é:
Esta aproximação fornece para z um erro absoluto máximo de 0,026 (para 0,5 ≤ p ≤ 0,9999, correspondente a 0 ≤ z ≤ 3,719). Para p < 1/2 substitua p por 1 − p e mude o sinal. Outra aproximação, um pouco menos precisa, é a aproximação de parâmetro único:
Esta última serviu para derivar uma aproximação simples para a integral de perda da distribuição normal, definida por
Esta aproximação é particularmente precisa para a cauda distante direita (erro máximo de 10−3 para z≥1.4). Aproximações altamente precisas para o CDF, com base na Metodologia de Modelagem de Resposta (RMM, Shore, 2011, 2012), são mostradas em Shore (2005).
Mais aproximações podem ser encontradas em: Função de erro#Aproximação com funções elementares. Em particular, pequeno relativo erro em todo o domínio para o CDF Φ Φ Não. Não. e a função quantil Φ Φ - Sim. - Sim. 1Não. Phi ^{-1}} também, é alcançado através de uma fórmula explicitamente invertível por Sergei Winitzki em 2008.
História
Desenvolvimento
Alguns autores atribuem o crédito pela descoberta da distribuição normal a de Moivre, que em 1738 publicou na segunda edição de seu "A Doutrina das Chances" o estudo dos coeficientes na expansão binomial de (um + b))n. De Moivre provou que o termo médio nesta expansão tem a magnitude aproximada de 2n/2D D n{textstyle 2^{n}/{sqrt {2pi n}}}e aquele "Se m ou 1/2n ser uma Quantidade infinitamente grande, então o Logarithm da Relação, que um Termo distante do meio pela Interval Eu..., tem a médio prazo, é - Sim. - Sim. 2Eu... Eu... Eu... Eu... n- Sim." Embora este teorema possa ser interpretado como a primeira expressão obscura para a lei de probabilidade normal, Stigler aponta que o próprio de Moivre não interpretou seus resultados como nada mais do que a regra aproximada para os coeficientes binomiais, e em particular de Moivre não tinha o conceito da função densidade de probabilidade.
Em 1823, Gauss publicou sua monografia "Theoria combinaçãois observationum erroribus minimis obnoxiae" onde, entre outras coisas, ele introduz vários conceitos estatísticos importantes, como o método dos mínimos quadrados, o método da máxima verossimilhança e a distribuição normal. Gauss usou M, M′, M′ ′,... para denotar as medidas de alguma quantidade desconhecida V, e buscou o "mais provável" estimador dessa quantidade: aquele que maximiza a probabilidade φ(M − V) · φ(M′ − V) · φ(M′′ − V ) ·... de obtenção dos resultados experimentais observados. Em sua notação φΔ é a função de densidade de probabilidade dos erros de medição de magnitude Δ. Sem saber o que é a função φ, Gauss exige que seu método se reduza à conhecida resposta: a média aritmética dos valores medidos. Partindo desses princípios, Gauss demonstra que a única lei que racionaliza a escolha da média aritmética como estimador do parâmetro de localização é a lei normal dos erros:
Embora Gauss tenha sido o primeiro a sugerir a lei de distribuição normal, Laplace fez contribuições significativas. Foi Laplace quem primeiro colocou o problema de agregar várias observações em 1774, embora sua própria solução tenha levado à distribuição Laplaciana. Foi Laplace quem primeiro calculou o valor da integral ∫ e−t2 dt = √π em 1782, fornecendo a constante de normalização para a distribuição normal. Finalmente, foi Laplace quem em 1810 provou e apresentou à Academia o teorema fundamental do limite central, que enfatizou a importância teórica da distribuição normal.
É interessante notar que em 1809 um matemático irlandês-americano Robert Adrain publicou duas derivações perspicazes, mas falhas, da lei de probabilidade normal, simultaneamente e independentemente de Gauss. Suas obras permaneceram praticamente despercebidas pela comunidade científica, até que em 1871 foram exumadas por Abbe.
Em meados do século 19, Maxwell demonstrou que a distribuição normal não é apenas uma ferramenta matemática conveniente, mas também pode ocorrer em fenômenos naturais: "O número de partículas cuja velocidade, resolvida em uma certa direção, reside entre x e x + dx é
Nomeando
Hoje, o conceito é geralmente conhecido em inglês como distribuição normal ou distribuição gaussiana. Outros nomes menos comuns incluem distribuição de Gauss, distribuição de Laplace-Gauss, lei do erro, lei da facilidade de erros, segunda lei de Laplace, lei gaussiana.
O próprio Gauss aparentemente cunhou o termo com referência às "equações normais" envolvido em suas aplicações, com normal tendo seu significado técnico de ortogonal em vez de "usual". No entanto, no final do século XIX alguns autores começaram a usar o nome distribuição normal, onde a palavra "normal" foi usado como adjetivo – o termo agora é visto como um reflexo do fato de que essa distribuição era vista como típica, comum – e, portanto, "normal". Peirce (um desses autores) certa vez definiu o termo "normal" assim: "...o 'normal' não é a média (ou qualquer outro tipo de média) do que realmente ocorre, mas do que iria, no longo prazo, ocorrer sob certas circunstâncias." Por volta da virada do século 20, Pearson popularizou o termo normal como uma designação para essa distribuição.
Muitos anos atrás eu chamei a curva Laplace-Gaussian a normal curva, que nome, embora evite uma questão internacional de prioridade, tem a desvantagem de levar as pessoas a acreditar que todas as outras distribuições de frequência estão em um sentido ou outro 'abnormal'.
—Pearson (1920)
Além disso, foi Pearson quem primeiro escreveu a distribuição em termos do desvio padrão σ como na notação moderna. Logo depois, no ano de 1915, Fisher adicionou o parâmetro de localização à fórmula da distribuição normal, expressando-a da forma como é escrita atualmente:
O termo "normal padrão", que denota a distribuição normal com média zero e variância unitária, tornou-se de uso geral por volta da década de 1950, aparecendo nos livros populares de P. G. Hoel (1947) &# 34;Introdução à estatística matemática" e A. M. Mood (1950) "Introdução à teoria da estatística".
Contenido relacionado
Icosaedro regular
Função de distribuição cumulativa
Álgebra alternativa





































![[-x,x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e23c41ff0bd6f01a0e27054c2b85819fcd08b762)

![{displaystyle Phi (x)={frac {1}{2}}left[1+operatorname {erf} left({frac {x}{sqrt {2}}}right)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7831a9a5f630df7170fa805c186f4c53219ca36)

![{displaystyle F(x)=Phi left({frac {x-mu }{sigma }}right)={frac {1}{2}}left[1+operatorname {erf} left({frac {x-mu }{sigma {sqrt {2}}}}right)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75deccfbc473d782dacb783f1524abb09b8135c0)





![{displaystyle Phi (x)={frac {1}{2}}+{frac {1}{sqrt {2pi }}}cdot e^{-x^{2}/2}left[x+{frac {x^{3}}{3}}+{frac {x^{5}}{3cdot 5}}+cdots +{frac {x^{2n+1}}{(2n+1)!!}}+cdots right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54d12af9a3b12a7f859e4e7be105d172b53bcfb8)



















































![{displaystyle operatorname {E} left[(X-mu)^{p}right]={begin{cases}0&{text{if }}p{text{ is odd,}}\sigma ^{p}(p-1)!!&{text{if }}p{text{ is even.}}end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1d2c92b62ac2bbe07a8e475faac29c8cc5f7755)



![{displaystyle {begin{aligned}operatorname {E} left[|X-mu |^{p}right]&=sigma ^{p}(p-1)!!cdot {begin{cases}{sqrt {frac {2}{pi }}}&{text{if }}p{text{ is odd}}\1&{text{if }}p{text{ is even}}end{cases}}\&=sigma ^{p}cdot {frac {2^{p/2}Gamma left({frac {p+1}{2}}right)}{sqrt {pi }}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b196371c491676efa7ea7770ef56773db7652cd)



![{displaystyle {begin{aligned}operatorname {E} left[X^{p}right]&=sigma ^{p}cdot (-i{sqrt {2}})^{p}Uleft(-{frac {p}{2}},{frac {1}{2}},-{frac {1}{2}}left({frac {mu }{sigma }}right)^{2}right),\operatorname {E} left[|X|^{p}right]&=sigma ^{p}cdot 2^{p/2}{frac {Gamma left({frac {1+p}{2}}right)}{sqrt {pi }}}{}_{1}F_{1}left(-{frac {p}{2}},{frac {1}{2}},-{frac {1}{2}}left({frac {mu }{sigma }}right)^{2}right).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c17bf881593b86e728bf5dfbdb41a4b86da3875)











![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)









![{displaystyle M(t)=operatorname {E} [e^{tX}]={hat {f}}(it)=e^{mu t}e^{{tfrac {1}{2}}sigma ^{2}t^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04bbd225c0fee5e58e9a8cd73b0f1b2bf535dc56)











































































































![{displaystyle t={frac {{overline {X}}-mu }{S/{sqrt {n}}}}={frac {{frac {1}{n}}(X_{1}+cdots +X_{n})-mu }{sqrt {{frac {1}{n(n-1)}}left[(X_{1}-{overline {X}})^{2}+cdots +(X_{n}-{overline {X}})^{2}right]}}}sim t_{n-1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36ff0d3c79a0504e8f259ef99192b825357914d7)















![{displaystyle operatorname {T} (X)={sqrt {frac {2}{pi }}}(sigma _{2}-sigma _{1})left[left({frac {4}{pi }}-1right)(sigma _{2}-sigma _{1})^{2}+sigma _{1}sigma _{2}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9959f2c5186e2ed76884054edaf837a602ac6fac)


















![{displaystyle mu in left[{hat {mu }}-t_{n-1,1-alpha /2}{frac {1}{sqrt {n}}}s,{hat {mu }}+t_{n-1,1-alpha /2}{frac {1}{sqrt {n}}}sright],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6e3068587bfbaf61a549a39b518757119bfb846)
![{displaystyle sigma ^{2}in left[{frac {(n-1)s^{2}}{chi _{n-1,1-alpha /2}^{2}}},{frac {(n-1)s^{2}}{chi _{n-1,alpha /2}^{2}}}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3549a31cb861d9e479c232271cb88b019cfa9fd5)
![{displaystyle mu in left[{hat {mu }}-|z_{alpha /2}|{frac {1}{sqrt {n}}}s,{hat {mu }}+|z_{alpha /2}|{frac {1}{sqrt {n}}}sright],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e13883f93c0a1405e71bd105685ecac6b4c84089)
![{displaystyle sigma ^{2}in left[s^{2}-|z_{alpha /2}|{frac {sqrt {2}}{sqrt {n}}}s^{2},s^{2}+|z_{alpha /2}|{frac {sqrt {2}}{sqrt {n}}}s^{2}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3e7c940eb3f6f50af62200ae75e10435ef8dfe6)

















![{displaystyle {begin{aligned}p(mathbf {X} mid mutau)&=prod _{i=1}^{n}{sqrt {frac {tau }{2pi }}}exp left(-{frac {1}{2}}tau (x_{i}-mu)^{2}right)\&=left({frac {tau }{2pi }}right)^{n/2}exp left(-{frac {1}{2}}tau sum _{i=1}^{n}(x_{i}-mu)^{2}right)\&=left({frac {tau }{2pi }}right)^{n/2}exp left[-{frac {1}{2}}tau left(sum _{i=1}^{n}(x_{i}-{bar {x}})^{2}+n({bar {x}}-mu)^{2}right)right].end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2bcd1c34520a24e29b758a0f7427e79e9d8a414)
![{displaystyle {begin{aligned}p(mu mid mathbf {X})&propto p(mathbf {X} mid mu)p(mu)\&=left({frac {tau }{2pi }}right)^{n/2}exp left[-{frac {1}{2}}tau left(sum _{i=1}^{n}(x_{i}-{bar {x}})^{2}+n({bar {x}}-mu)^{2}right)right]{sqrt {frac {tau _{0}}{2pi }}}exp left(-{frac {1}{2}}tau _{0}(mu -mu _{0})^{2}right)\&propto exp left(-{frac {1}{2}}left(tau left(sum _{i=1}^{n}(x_{i}-{bar {x}})^{2}+n({bar {x}}-mu)^{2}right)+tau _{0}(mu -mu _{0})^{2}right)right)\&propto exp left(-{frac {1}{2}}left(ntau ({bar {x}}-mu)^{2}+tau _{0}(mu -mu _{0})^{2}right)right)\&=exp left(-{frac {1}{2}}(ntau +tau _{0})left(mu -{dfrac {ntau {bar {x}}+tau _{0}mu _{0}}{ntau +tau _{0}}}right)^{2}+{frac {ntau tau _{0}}{ntau +tau _{0}}}({bar {x}}-mu _{0})^{2}right)\&propto exp left(-{frac {1}{2}}(ntau +tau _{0})left(mu -{dfrac {ntau {bar {x}}+tau _{0}mu _{0}}{ntau +tau _{0}}}right)^{2}right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96e309ead00fbc8603eced5342aa5df534522d6a)



![{displaystyle {begin{aligned}tau _{0}'&=tau _{0}+ntau \[5pt]mu _{0}'&={frac {ntau {bar {x}}+tau _{0}mu _{0}}{ntau +tau _{0}}}\[5pt]{bar {x}}&={frac {1}{n}}sum _{i=1}^{n}x_{i}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6cfbdf504b1a9ce4cbe79561b4ae983fdf7271d)

![{displaystyle {begin{aligned}{sigma _{0}^{2}}'&={frac {1}{{frac {n}{sigma ^{2}}}+{frac {1}{sigma _{0}^{2}}}}}\[5pt]mu _{0}'&={frac {{frac {n{bar {x}}}{sigma ^{2}}}+{frac {mu _{0}}{sigma _{0}^{2}}}}{{frac {n}{sigma ^{2}}}+{frac {1}{sigma _{0}^{2}}}}}\[5pt]{bar {x}}&={frac {1}{n}}sum _{i=1}^{n}x_{i}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea454c8840683777ce8192d9ae63068c63962858)
![{displaystyle p(sigma ^{2}mid nu _{0},sigma _{0}^{2})={frac {(sigma _{0}^{2}{frac {nu _{0}}{2}})^{nu _{0}/2}}{Gamma left({frac {nu _{0}}{2}}right)}}~{frac {exp left[{frac {-nu _{0}sigma _{0}^{2}}{2sigma ^{2}}}right]}{(sigma ^{2})^{1+{frac {nu _{0}}{2}}}}}propto {frac {exp left[{frac {-nu _{0}sigma _{0}^{2}}{2sigma ^{2}}}right]}{(sigma ^{2})^{1+{frac {nu _{0}}{2}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef2528fe4774a93087d4adae570ef9ab84707f52)
![{displaystyle {begin{aligned}p(mathbf {X} mid musigma ^{2})&=left({frac {1}{2pi sigma ^{2}}}right)^{n/2}exp left[-{frac {1}{2sigma ^{2}}}sum _{i=1}^{n}(x_{i}-mu)^{2}right]\&=left({frac {1}{2pi sigma ^{2}}}right)^{n/2}exp left[-{frac {S}{2sigma ^{2}}}right]end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc06aa31588bba03e4748f8f345f0638a75dc156)

![{displaystyle {begin{aligned}p(sigma ^{2}mid mathbf {X})&propto p(mathbf {X} mid sigma ^{2})p(sigma ^{2})\&=left({frac {1}{2pi sigma ^{2}}}right)^{n/2}exp left[-{frac {S}{2sigma ^{2}}}right]{frac {(sigma _{0}^{2}{frac {nu _{0}}{2}})^{frac {nu _{0}}{2}}}{Gamma left({frac {nu _{0}}{2}}right)}}~{frac {exp left[{frac {-nu _{0}sigma _{0}^{2}}{2sigma ^{2}}}right]}{(sigma ^{2})^{1+{frac {nu _{0}}{2}}}}}\&propto left({frac {1}{sigma ^{2}}}right)^{n/2}{frac {1}{(sigma ^{2})^{1+{frac {nu _{0}}{2}}}}}exp left[-{frac {S}{2sigma ^{2}}}+{frac {-nu _{0}sigma _{0}^{2}}{2sigma ^{2}}}right]\&={frac {1}{(sigma ^{2})^{1+{frac {nu _{0}+n}{2}}}}}exp left[-{frac {nu _{0}sigma _{0}^{2}+S}{2sigma ^{2}}}right]end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/381c1b93f6dc76e2cdca9f3f1f77132dd51dc55f)






![{displaystyle {begin{aligned}p(mu mid sigma ^{2};mu _{0},n_{0})&sim {mathcal {N}}(mu _{0},sigma ^{2}/n_{0})={frac {1}{sqrt {2pi {frac {sigma ^{2}}{n_{0}}}}}}exp left(-{frac {n_{0}}{2sigma ^{2}}}(mu -mu _{0})^{2}right)\&propto (sigma ^{2})^{-1/2}exp left(-{frac {n_{0}}{2sigma ^{2}}}(mu -mu _{0})^{2}right)\p(sigma ^{2};nu _{0},sigma _{0}^{2})&sim Ichi ^{2}(nu _{0},sigma _{0}^{2})=IG(nu _{0}/2,nu _{0}sigma _{0}^{2}/2)\&={frac {(sigma _{0}^{2}nu _{0}/2)^{nu _{0}/2}}{Gamma (nu _{0}/2)}}~{frac {exp left[{frac {-nu _{0}sigma _{0}^{2}}{2sigma ^{2}}}right]}{(sigma ^{2})^{1+nu _{0}/2}}}\&propto {(sigma ^{2})^{-(1+nu _{0}/2)}}exp left[{frac {-nu _{0}sigma _{0}^{2}}{2sigma ^{2}}}right].end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf7afb8e3b63fb1526171840344b32458e55cf8b)
![{displaystyle {begin{aligned}p(musigma ^{2};mu _{0},n_{0},nu _{0},sigma _{0}^{2})&=p(mu mid sigma ^{2};mu _{0},n_{0}),p(sigma ^{2};nu _{0},sigma _{0}^{2})\&propto (sigma ^{2})^{-(nu _{0}+3)/2}exp left[-{frac {1}{2sigma ^{2}}}left(nu _{0}sigma _{0}^{2}+n_{0}(mu -mu _{0})^{2}right)right].end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6f808161077baef3854dbfd90b870698d721090)
![{begin{aligned}p(mathbf {X} mid musigma ^{2})&=left({frac {1}{2pi sigma ^{2}}}right)^{n/2}exp left[-{frac {1}{2sigma ^{2}}}left(sum _{i=1}^{n}(x_{i}-mu)^{2}right)right]end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3d77342aadcb34c5d84418cecaefdb52842b6b7)
![{begin{aligned}p(mathbf {X} mid musigma ^{2})&=left({frac {1}{2pi sigma ^{2}}}right)^{n/2}exp left[-{frac {1}{2sigma ^{2}}}left(sum _{i=1}^{n}(x_{i}-{bar {x}})^{2}+n({bar {x}}-mu)^{2}right)right]\&propto {sigma ^{2}}^{-n/2}exp left[-{frac {1}{2sigma ^{2}}}left(S+n({bar {x}}-mu)^{2}right)right]end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29b915f070b522a1e9f419be05624c86c854ca14)

![{begin{aligned}p(musigma ^{2}mid mathbf {X})&propto p(musigma ^{2}),p(mathbf {X} mid musigma ^{2})\&propto (sigma ^{2})^{-(nu _{0}+3)/2}exp left[-{frac {1}{2sigma ^{2}}}left(nu _{0}sigma _{0}^{2}+n_{0}(mu -mu _{0})^{2}right)right]{sigma ^{2}}^{-n/2}exp left[-{frac {1}{2sigma ^{2}}}left(S+n({bar {x}}-mu)^{2}right)right]\&=(sigma ^{2})^{-(nu _{0}+n+3)/2}exp left[-{frac {1}{2sigma ^{2}}}left(nu _{0}sigma _{0}^{2}+S+n_{0}(mu -mu _{0})^{2}+n({bar {x}}-mu)^{2}right)right]\&=(sigma ^{2})^{-(nu _{0}+n+3)/2}exp left[-{frac {1}{2sigma ^{2}}}left(nu _{0}sigma _{0}^{2}+S+{frac {n_{0}n}{n_{0}+n}}(mu _{0}-{bar {x}})^{2}+(n_{0}+n)left(mu -{frac {n_{0}mu _{0}+n{bar {x}}}{n_{0}+n}}right)^{2}right)right]\&propto (sigma ^{2})^{-1/2}exp left[-{frac {n_{0}+n}{2sigma ^{2}}}left(mu -{frac {n_{0}mu _{0}+n{bar {x}}}{n_{0}+n}}right)^{2}right]\&quad times (sigma ^{2})^{-(nu _{0}/2+n/2+1)}exp left[-{frac {1}{2sigma ^{2}}}left(nu _{0}sigma _{0}^{2}+S+{frac {n_{0}n}{n_{0}+n}}(mu _{0}-{bar {x}})^{2}right)right]\&={mathcal {N}}_{mu mid sigma ^{2}}left({frac {n_{0}mu _{0}+n{bar {x}}}{n_{0}+n}},{frac {sigma ^{2}}{n_{0}+n}}right)cdot {rm {IG}}_{sigma ^{2}}left({frac {1}{2}}(nu _{0}+n),{frac {1}{2}}left(nu _{0}sigma _{0}^{2}+S+{frac {n_{0}n}{n_{0}+n}}(mu _{0}-{bar {x}})^{2}right)right).end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cad9489034d77d53c12c7ee6044f712cfdb77831)



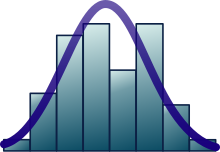





![{displaystyle z=Phi ^{-1}(p)=5.5556left[1-left({frac {1-p}{p}}right)^{0.1186}right],qquad pgeq 1/2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f2df7f1427d0c90d075faef38f4f5ab7acce5c9)
![{displaystyle z=-0.4115left{{frac {1-p}{p}}+log left[{frac {1-p}{p}}right]-1right},qquad pgeq 1/2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1edea9f990058f741db6735799c8b40999b833b)







