Cubo

Hexahedron regular
(Clique aqui para girar modelo)
Tipo	sólido platônico
Elementos	F - 6, E = 12 V = 8 (χ = 2)
Faces por lados	6
Notação de saída	C
Símbolos de Schläfli	{4,3}
	T{2,4} ou {4} × Não. Não.3
Configuração da face	V3.3.3.3
Símbolo de Wythoff	3 | 2 4
Diagrama de Coxeador
Simetria	Oh, B3[4,3], (*432)
Grupo de rotação	[4,3]+, (432)
Referências	U06:06C18.,3
Propriedades	regular, convexzonohedron, Hanner politope
Ângulo dihedral	90°
4.4.4 (Vertex figure)	Octaedron (poliédron dual)
Rede

Rede de um cubo

Modelo 3D de um cubo

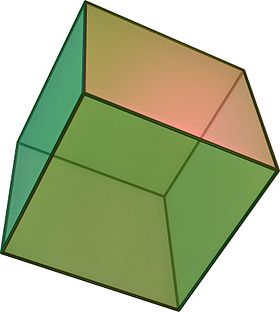
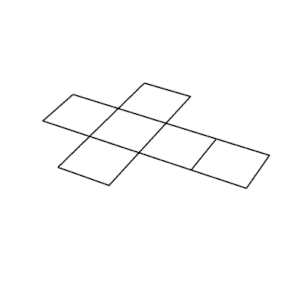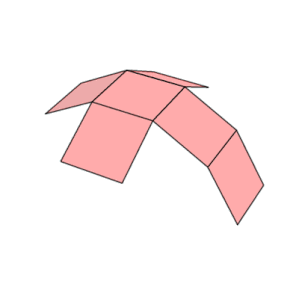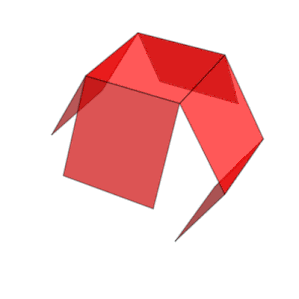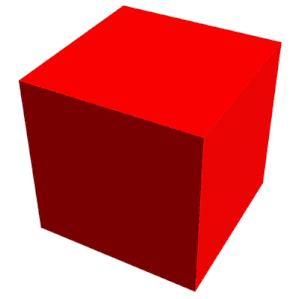
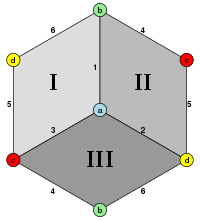
Na geometria, um cubo é um objeto sólido tridimensional delimitado por seis faces quadradas, facetas ou lados, com três encontros em cada vértice. Visto de um canto, é um hexágono e sua rede geralmente é representada como uma cruz.

O cubo é o único hexaedro regular e é um dos cinco sólidos platônicos. Tem 6 faces, 12 arestas e 8 vértices.

O cubo é também um paralelepípedo quadrado, um paralelepípedo equilátero e um romboedro reto um 3-zonoedro. É um prisma quadrado regular em três orientações e um trapezoedro trigonal em quatro orientações.

O cubo é dual ao octaedro. Tem simetria cúbica ou octaédrica.

O cubo é o único poliedro convexo cujas faces são todas quadradas.

Projeções ortogonais

O cubo tem quatro projeções ortogonais especiais, centradas, em um vértice, arestas, face e normal à sua figura de vértice. O primeiro e o terceiro correspondem aos planos A₂ e B₂ de Coxeter.

Projeções ortogonais

Centro por	Cara	Verbos
Aviões de Coxeter	B2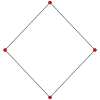	A2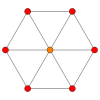
Projeto simetria	[4]	[6]
Vistas inclinadas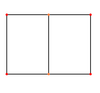

Telha esférica

O cubo também pode ser representado como um ladrilho esférico e projetado no plano por meio de uma projeção estereográfica. Essa projeção é conforme, preservando ângulos, mas não áreas ou comprimentos. Linhas retas na esfera são projetadas como arcos circulares no plano.

Projeção ortográfico	Projeção estereográfica

Coordenadas cartesianas

Para um cubo centrado na origem, com arestas paralelas aos eixos e comprimento de aresta igual a 2, as coordenadas cartesianas dos vértices são

(±1, ±1, ±1)

enquanto o interior consiste em todos os pontos (x₀, x₁, x₂) com −1 < x_i < 1 para todos os i.

Equação no espaço tridimensional

Na geometria analítica, a superfície de um cubo com centro (x₀, y₀, z₀) e o comprimento da aresta de 2a é o lugar geométrico de todos os pontos (x, y , z) tal que

máx.(|x- Sim. - Sim. x0|,|Sim.- Sim. - Sim. Sim.0|,|zangão.- Sim. - Sim. zangão.0|?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um.{displaystyle max{|x-x_{0}|,|y-y_{0}|,|z-z_{0}|}=a.}

Um cubo também pode ser considerado o caso limite de um superelipsóide 3D, pois todos os três expoentes se aproximam do infinito.

Fórmulas

Para um cubo de comprimento da borda umNão.:

área de superfície	6um2{displaystyle 6a^{2},}	volume	um3{displaystyle a^{3},}
face diagonal	2um(2}}a)	espaço diagonal	3um- Sim. Não.
raio de esfera circunscrita	32umNão. {3}}{2}}a)	raio de esfera tangente a bordas	um2Não. {2}}
raio de esfera inscrita	um2- Sim.	ângulos entre rostos (em radianos)	D D 2Não. ?

Como o volume de um cubo é o terceiro poder de seus lados um× × um× × um{displaystyle atimes atimes a}, terceiro poderes são chamados cubos, por analogia com quadrados e segundo poderes.

Um cubo tem o maior volume entre os cubóides (caixas retangulares) com uma determinada área de superfície. Além disso, um cubo tem o maior volume entre os cuboides com o mesmo tamanho linear total (comprimento+largura+altura).

Ponto no espaço

Para um cubo cuja esfera circunscrita tem raio R, e para um dado ponto em seu espaço tridimensional com distâncias d_i de os oito vértices do cubo, temos:

Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =18DEu...48+16.R49= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(Gerenciamento Gerenciamento Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =18DEu...28+2R23)2.- Sim. _{i=1}^{8}d_{i}^{4}}{8}}+{frac {16R^{4}}{9}}=left({frac {sum _{i=1}^{8}d_{i}^{2}}{8}}+{frac {2R^{2}}{3}}right)^{2}.}

Duplicando o cubo

Duplicar o cubo, ou o problema de Delian, foi o problema colocado pelos antigos matemáticos gregos de usar apenas compasso e régua para começar com o comprimento da aresta de um dado cubo e construir o comprimento da aresta de um cubo com o dobro do volume do cubo original. Eles não conseguiram resolver esse problema, que em 1837 Pierre Wantzel provou ser impossível porque a raiz cúbica de 2 não é um número construível.

Cores uniformes e simetria

Árvore de simetria Octaedral

O cubo tem três cores uniformes, nomeadas pelas cores únicas das faces quadradas em torno de cada vértice: 111, 112, 123.

O cubo tem quatro classes de simetria, que podem ser representadas pela coloração transitiva dos vértices das faces. A maior simetria octaédrica O_h tem todas as faces da mesma cor. A simetria diedral D_4h vem do cubo sendo um sólido, com todos os seis lados sendo de cores diferentes. O subconjunto prismático D_2d tem a mesma coloração do anterior e D_2h tem cores alternadas para seus lados para um total de três cores, emparelhadas por lados opostos. Cada forma de simetria tem um símbolo Wythoff diferente.

Nome	Regular Hexahedron	Praça prisma	Retangular Articulação	Retangularcuboid	Rhombic O que é?	Trigonal Armadilha
Medidores de água
Produtos de plástico	{4,3}	Não. rr{4,2}	S2(2,4)	Não.3 Não.	- Não.
- Sim.	3 | 4 2	4 2 | 2		2 2 2 |
Simetria	Oh [4,3] (*432)	D4h [4,2] (*422)	D2d [4]+] (2*2)	D2h [2,2] (*222)		D3D [6,2]+] (2*3)
Simetria ordem	24.	16.	8	8		12
Imagem (uniformidade coloração)	(111)	(112)	(112)	(123)	(112)	(111), (112)

Relações geométricas

As 11 redes do cubo

Estes dados familiares de seis lados são em forma de cubo.

Um cubo tem onze redes (uma mostrada acima): ou seja, existem onze maneiras de achatar um cubo oco cortando sete arestas. Para colorir o cubo de modo que não haja duas faces adjacentes com a mesma cor, seriam necessárias pelo menos três cores.

O cubo é a célula do único ladrilho regular do espaço euclidiano tridimensional. Também é único entre os sólidos platônicos por ter faces com número par de lados e, conseqüentemente, é o único membro desse grupo que é um zonoedro (toda face tem simetria pontual).

O cubo pode ser cortado em seis pirâmides quadradas idênticas. Se essas pirâmides quadradas forem então ligadas às faces de um segundo cubo, obtém-se um dodecaedro rômbico (com pares de triângulos coplanares combinados em faces rômbicas).

Em Teologia

Os cubos aparecem nas religiões abraâmicas. A Kaaba em Meca é um exemplo que é árabe para "o cubo". Eles também aparecem no judaísmo como Teffilin e a Nova Jerusalém no Novo Testamento também é descrita como sendo um cubo.

Outras dimensões

O análogo de um cubo no espaço euclidiano quadridimensional tem um nome especial - um tesserato ou hipercubo. Mais propriamente, um hipercubo (ou cubo n-dimensional ou simplesmente n-cubo) é o análogo do cubo no espaço euclidiano n-dimensional e um tesserato é o hipercubo de ordem 4. Um hipercubo também é chamado de politopo de medida.

Também existem análogos do cubo em dimensões inferiores: um ponto na dimensão 0, um segmento de linha em uma dimensão e um quadrado em duas dimensões.

Polyedros relacionados

O duplo de um cubo é um octahedron, visto aqui com vértices no centro das faces quadradas do cubo.

O hemicube é o quociente de 2 a 1 do cubo.

O quociente do cubo pelo mapa antípoda produz um poliedro projetivo, o hemicubo.

Se o cubo original tem comprimento de borda 1, seu poliedro duplo (um octahedron) tem comprimento de borda 2/2{displaystyle scriptstyle {sqrt {2}/2}.

O cubo é um caso especial em várias classes de poliedros gerais:

Os vértices de um cubo podem ser agrupados em dois grupos de quatro, cada um formando um tetraedro regular; mais geralmente, isso é chamado de demicubo. Esses dois juntos formam um composto regular, a stella octangula. A interseção dos dois forma um octaedro regular. As simetrias de um tetraedro regular correspondem àquelas de um cubo que mapeia cada tetraedro para si mesmo; as outras simetrias do cubo mapeiam as duas entre si.

Um desses tetraedros regulares tem um volume de 1/3 do cubo. O espaço restante consiste em quatro tetraedros irregulares iguais com um volume de 1 /6 do cubo, cada.

O cubo retificado é o cuboctaedro. Se os cantos menores forem cortados, obtemos um poliedro com seis faces octogonais e oito triangulares. Em particular, podemos obter octógonos regulares (cubo truncado). O rombicuboctaedro é obtido cortando ambos os cantos e bordas na quantidade correta.

Um cubo pode ser inscrito em um dodecaedro de modo que cada vértice do cubo seja um vértice do dodecaedro e cada aresta seja uma diagonal de uma das faces do dodecaedro; pegar todos esses cubos dá origem ao composto regular de cinco cubos.

Se dois cantos opostos de um cubo são truncados na profundidade dos três vértices diretamente conectados a eles, um octaedro irregular é obtido. Oito desses octaedros irregulares podem ser anexados às faces triangulares de um octaedro regular para obter o cuboctaedro.

O cubo está topologicamente relacionado a uma série de poliédricos esféricos e ladrilhos com figuras de vértices de ordem 3.

*n32 mutação simetria de camadas regulares: (n,3 v ) e
Esférica				Euclidiano	Hiperb compacto.		Paraco.	Hiperbólico não-compacto
(2,3)	(3,3)	{4,3}	{5,3}	Não.	{7,3}	(8,3)	{∞,3}	(12i,3)	(9i,3)	(6i,3)	(3i,3)

O cuboctaedro faz parte de uma família de poliedros uniformes relacionados ao cubo e ao octaedro regular.

Poliedros octahedral uniforme
Simetria: [4,3], (*432)							[4,3]+ (432)	[2]+[3,3] (*332)		[3]+,4] (3*2)
{4,3}	Não.	R{4,3} RECURSOS1.1?	T3,4 )1.1?	{3,4} (1.1?	rr,3 S2{3,4}	Não.	Sr.	H{4,3} (3,3)	H2{4,3} T3,3	- Sim. )1.1?
		= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =	= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =	= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =				= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = ou	= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = ou	= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =
Duals para polihedra uniforme
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V3	V3.62	V35

O cubo é topologicamente relacionado como parte de uma sequência de ladrilhos regulares, estendendo-se ao plano hiperbólico: {4,p}, p=3,4,5...

*n42 mutação simetria de tilins regulares: (n? v ) e
Esférica	Euclidiano	Hiperbólica compacta				Paracompactar
{4,3}	(4,4)	(4,5)	(4,6)	{4,7}	(4,8}...	(4,∞)

Com simetria diédrica, Dih₄, o cubo é topologicamente relacionado em uma série de poliédricos uniformes e ladrilhos 4.2n.2n, estendendo-se no plano hiperbólico:

*n42 mutação simetria de tilins truncados: - Sim.n.2n v ) e
Simetria *n42 [n]	Esférica		Euclidiano	Hiperbólica compacta				Paracomp.
	*242 [2,4]	*342 [3,4]	*442 [4]	* 542 [5]	* 642 [6]	*742 [7]	* 842 [8,4]...	* ∞42 [∞,4]
Truncado números
Config.	4.4.4	4.6.	4.8.8	4.10.10	4.12.19	4.14.14	4.16.16	4.∞.∞
n-kis números
Config.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.	V4.14.14	V4.16.16	V4.∞.∞

Todas essas figuras têm simetria octaédrica.

O cubo faz parte de uma sequência de poliedros rômbicos e ladrilhos com [n,3] simetria do grupo de Coxeter. O cubo pode ser visto como um hexaedro rômbico onde os losangos são quadrados.

Mutações de simetria de camadas quasiregulares duplas: V(3.n)2
*n32	Esférica			Euclidiano	Hyperbolic
	*332	*432	* 532	*632	*732	*832...	* ∞32
Inclinação
Conf.	V(3.3)2	V(3.4)2	V(3.5)2	V(3.6)2	V(3.7)2	V(3.8)2	V(3.∞)2

O cubo é um prisma quadrado:

Família de uniforme n- prismas gerais v ) e
Nome do prisma	Princípios gerais	(Trigonal) Prisma triangular	(Tetragonal) Praça prisma	Prisma Pentágono	Prisma hexagonal	Prisma heptagonal	Prisma octogonal	Enneagonal prisma	Prisma Decagonal	Prisma hendecagonal	Dodecagonal prisma	...	Prisma Apeirogonal
Imagem de poliedro												...
Imagem de tilagem esférica												Imagem de tilingue plana
Configuração do vértice.	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	...	∞.4.4
Diagrama de Coxeador												...

Como um trapezoedro trigonal, o cubo está relacionado com a família de simetria diédrica hexagonal.

Polihedra esférico hexagonal dihedral uniforme
Simetria: [6,2], (*622)							[6,2]+(622)	[6,2]+(2)
Não.	Não.	R{6,2}	T2,6	(2,6)	rr{6,2}	Não.	Sr.	S{2,6}
Duals a uniformes
V62	V122	V62	V4.4.6	V.	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Compostos regulares e uniformes de cubos

Composto de três cubos

Composto de cinco cubos

Em favos de mel uniformes e polychora

É um elemento de 9 de 28 favos de mel uniformes convexos:

Bebê de mel cúbico	favo de mel prismático quadrado truncado	Comboio de mel prismático quadrado Snub	Combola de mel prismática triangular alongada	Madressilva prismática triangular alongada
favo de mel cúbico velada	Cantitruncado favo de mel cúbico	Comboio de mel cúbico Runcitrunca	favo de mel cúbico alternativo Runcinated

É também um elemento de cinco polychora uniformes quadridimensionais:

Tesseract	Cantela de 16 células	Tesseract	Cantitruncated 16-cell	Runcitruncated 16-cell

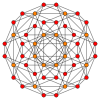Gráfico cúbico

O esqueleto do cubo (os vértices e as arestas) forma um grafo com 8 vértices e 12 arestas, denominado grafo do cubo. É um caso especial do grafo hipercubo. É um dos 5 grafos platônicos, cada um um esqueleto de seu sólido platônico.

Uma extensão é o grafo de Hamming k-ARY tridimensional, que para k = 2 é o grafo do cubo. Gráficos desse tipo ocorrem na teoria do processamento paralelo em computadores.