Conjunto de cantores

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Conjunto de pontos em um segmento de linha

Na matemática, o conjunto de Cantor é um conjunto de pontos situados em um único segmento de linha que possui várias propriedades não intuitivas. Foi descoberto em 1874 por Henry John Stephen Smith e introduzido pelo matemático alemão Georg Cantor em 1883.

Através da consideração desse conjunto, Cantor e outros ajudaram a estabelecer as bases da topologia moderna de conjuntos de pontos. A construção mais comum é o conjunto ternário de Cantor, construído removendo o terço médio de um segmento de linha e repetindo o processo com os segmentos menores restantes. Cantor mencionou a construção ternária apenas de passagem, como exemplo de uma ideia mais geral, a de um conjunto perfeito que não é denso em parte alguma.

De forma mais geral, em topologia, um espaço de Cantor é um espaço topológico homeomorfo ao conjunto ternário de Cantor (equipado com sua topologia de subespaço). Por um teorema de Brouwer, isso equivale a ser perfeito não vazio, compacto metrizável e zero dimensional.

Zoom em conjunto Cantor. Cada ponto no conjunto é representado aqui por uma linha vertical.

Construção e fórmula do conjunto ternário

O conjunto de ternary Cantor ${mathcal {C}}$ é criado pela eliminação iterativa do terço médio aberto de um conjunto de segmentos de linha. Um começa apagando o terceiro meio aberto ${textstyle left({frac {1}{3}},{frac {2}{3}}right)}$ do intervalo ${displaystyle textstyle left[0,1right]}$ , deixando dois segmentos de linha: ${textstyle left[0,{frac {1}{3}}right]cup left[{frac {2}{3}},1right]}$ . Em seguida, o terço médio aberto de cada um desses segmentos restantes é excluído, deixando quatro segmentos de linha: ${textstyle left[0,{frac {1}{9}}right]cup left[{frac {2}{9}},{frac {1}{3}}right]cup left[{frac {2}{3}},{frac {7}{9}}right]cup left[{frac {8}{9}},1right]}$ . O conjunto de ternário Cantor contém todos os pontos no intervalo $[0,1]$ que não são excluídos a qualquer passo neste processo infinito. Os mesmos fatos podem ser descritos recursivamente pela definição

{displaystyle C_{0}:=[0,1]}

{displaystyle C_{n}:={frac {C_{n-1}}{3}}cup left({frac {2}{3}}+{frac {C_{n-1}}{3}}right)={frac {1}{3}}{bigl (}C_{n-1}cup left(2+C_{n-1}right){bigr)}}

para $ngeq 1$ , para que

{displaystyle {mathcal {C}}:=}

{displaystyle {color {Blue}lim _{nto infty }C_{n}}}

{displaystyle =bigcap _{n=0}^{infty }C_{n}=bigcap _{n=m}^{infty }C_{n}}

para qualquer

mgeq 0

As seis primeiras etapas desse processo são ilustradas abaixo.

Usando a ideia de transformações auto-similar, ${displaystyle T_{L}(x)=x/3,}$ ${displaystyle T_{R}(x)=(2+x)/3}$ e ${displaystyle C_{n}=T_{L}(C_{n-1})cup T_{R}(C_{n-1}),}$ as fórmulas fechadas explícitas para o conjunto Cantor são

{displaystyle {mathcal {C}}=[0,1],setminus ,bigcup _{n=0}^{infty }bigcup _{k=0}^{3^{n}-1}left({frac {3k+1}{3^{n+1}}},{frac {3k+2}{3^{n+1}}}right)!,}

onde cada terço médio é removido como o intervalo aberto ${textstyle left({frac {3k+1}{3^{n+1}}},{frac {3k+2}{3^{n+1}}}right)}$ do intervalo fechado ${textstyle left[{frac {3k+0}{3^{n+1}}},{frac {3k+3}{3^{n+1}}}right]=left[{frac {k+0}{3^{n}}},{frac {k+1}{3^{n}}}right]}$ em torno dele, ou

{displaystyle {mathcal {C}}=bigcap _{n=1}^{infty }bigcup _{k=0}^{3^{n-1}-1}left(left[{frac {3k+0}{3^{n}}},{frac {3k+1}{3^{n}}}right]cup left[{frac {3k+2}{3^{n}}},{frac {3k+3}{3^{n}}}right]right)!,}

onde o terceiro meio ${textstyle left({frac {3k+1}{3^{n}}},{frac {3k+2}{3^{n}}}right)}$ do intervalo fechado precedente ${textstyle left[{frac {k+0}{3^{n-1}}},{frac {k+1}{3^{n-1}}}right]=left[{frac {3k+0}{3^{n}}},{frac {3k+3}{3^{n}}}right]}$ é removido por intersecção com ${textstyle left[{frac {3k+0}{3^{n}}},{frac {3k+1}{3^{n}}}right]cup left[{frac {3k+2}{3^{n}}},{frac {3k+3}{3^{n}}}right]!.}$

Este processo de remoção de terços do meio é um exemplo simples de uma regra de subdivisão finita. O complemento do conjunto ternário de Cantor é um exemplo de string fractal.

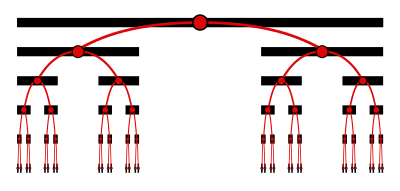
Em termos aritméticos, o conjunto Cantor consiste em todos os números reais do intervalo unitário $[0,1]$ que não exigem o dígito 1 para ser expresso como um ternário (base 3) fração. Como o diagrama acima ilustra, cada ponto no conjunto Cantor é exclusivamente localizado por um caminho através de uma árvore binária infinitamente profunda, onde o caminho vira para a esquerda ou para a direita em cada nível de acordo com qual lado de um segmento excluído o ponto está em. Representando cada curva esquerda com 0 e cada curva direita com 2 produz a fração ternary por um ponto.

Construção de Mandelbrot por "Curdling"

Em The Fractal Geometry of Nature, o matemático Benoit Mandelbrot fornece uma experiência de pensamento caprichoso para ajudar leitores não matemáticos a imaginar a construção de ${mathcal {C}}$ . Sua narrativa começa com a imaginação de um bar, talvez de metal leve, em que a matéria do bar "curdles" por iterativamente mudando para suas extremidades. À medida que os segmentos da barra tornam-se menores, tornam-se lesmas finas e densas que, eventualmente, crescem muito pequenas e fracas para ver.

CURDLING: A construção da barra de Cantor resulta do processo que eu chamo curdling. Começa com uma barra redonda. É melhor pensar nisso como tendo uma densidade muito baixa. Em seguida, importa “curdles” fora do terço médio desta barra para os terços finais, de modo que as posições do último permanecem inalteradas. A próxima matéria curdles fora do terço médio de cada terceiro final em seus terços finais, e assim em ad infinitum até que um é deixado com um número infinitamente grande de lesmas infinitamente finas de densidade infinitamente alta. Estas lesmas são espaçadas ao longo da linha da forma muito específica induzida pelo processo de geração. Nesta ilustração, a curvatura (que eventualmente requer martelar!) pára quando tanto a imprensa da impressora quanto o nosso olho deixam de seguir; a última linha é indistinguível do último, mas um: cada uma de suas partes finais é vista como uma lesma cinza ao invés de duas lesmas pretas paralelas. ”

Composição

Como o conjunto de Cantor é definido como o conjunto de pontos não excluídos, a proporção (ou seja, medida) do intervalo unitário restante pode ser encontrada pelo comprimento total removido. Esse total é a progressão geométrica

sum_{n=0}^infty frac{2^n}{3^{n+1}} = frac{1}{3} + frac{2}{9} + frac{4}{27} + frac{8}{81} + cdots = frac{1}{3}left(frac{1}{1-frac{2}{3}}right) = 1.

Para que a proporção restante seja 1 − 1 = 0.

Este cálculo sugere que o conjunto de Cantor não pode conter nenhum intervalo de comprimento diferente de zero. Pode parecer surpreendente que haja algo sobrando - afinal, a soma dos comprimentos dos intervalos removidos é igual ao comprimento do intervalo original. No entanto, um olhar mais atento ao processo revela que deve haver algo sobrando, já que remover o "terço do meio" de cada intervalo envolveu a remoção de conjuntos abertos (conjuntos que não incluem seus pontos finais). Portanto, removendo o segmento de linha (1/3, 2/3) do intervalo original [0, 1] deixa para trás os pontos 1/3 e 2/3 . As etapas subseqüentes não removem esses (ou outros) pontos finais, pois os intervalos removidos são sempre internos aos intervalos restantes. Portanto, o conjunto de Cantor não está vazio e, na verdade, contém um número incontável e infinito de pontos (como segue da descrição acima em termos de caminhos em uma árvore binária infinita).

Pode parecer que só restam os pontos finais dos segmentos de construção, mas também não é o caso. O número 1/4, por exemplo, tem a forma ternária única 0.020202... = 0.02. Está no terço inferior, no terço superior desse terço, no terço inferior do terço superior e assim por diante. Como nunca está em um dos segmentos intermediários, nunca é removido. No entanto, também não é um ponto final de nenhum segmento intermediário, porque não é um múltiplo de nenhuma potência de 1/3. Todas as extremidades dos segmentos são frações ternárias terminantes e estão contidas no conjunto

{displaystyle left{xin [0,1]mid exists iin mathbb {N} _{0}:x,3^{i}in mathbb {Z} right}qquad {Bigl (}subset mathbb {N} _{0},3^{-mathbb {N} _{0}}{Bigr)}}

, que é um conjunto de contagens infinitas. Quanto à cardinalidade, quase todos os elementos do conjunto de Cantor não são pontos finais de intervalos, nem pontos racionais como 1/4. Todo o conjunto de Cantor não é contável.

Propriedades

cardinalidade

Pode-se mostrar que há tantos pontos deixados para trás neste processo como havia para começar, e que, portanto, o conjunto Cantor é incontável. Para ver isso, mostramos que há uma função f do conjunto Cantor ${mathcal {C}}$ ao intervalo fechado [0,1] que é subjetivo (i.e. f mapas de ${mathcal {C}}$ para [0,1]) para que a cardinalidade de ${mathcal {C}}$ não é menos do que o de [0,1]. Desde então ${mathcal {C}}$ é um subconjunto de [0,1], sua cardinalidade também não é maior, então as duas cardinalidades devem, de fato, ser iguais, pelo teorema de Cantor-Bernstein-Schröder.

Para construir esta função, considere os pontos no intervalo [0, 1] em termos de notação base 3 (ou ternário). Lembre-se de que as frações ternárias adequadas, mais precisamente: os elementos de ${displaystyle {bigl (}mathbb {Z} setminus {0}{bigr)}cdot 3^{-mathbb {N} _{0}}}$ , admitir mais de uma representação nesta notação, como por exemplo 1/3, que pode ser escrito como 0.1₃ = 0,10₃, mas também como 0,0222...₃ = 0,02₃e 2/3, que pode ser escrito como 0.2₃ = 0,20₃ mas também como 0.1222...₃ = 0,12₃. Quando removemos o terço médio, isso contém os números com números ternary do formulário 0.1xxxx...₃ onde xxxxx...₃ é estritamente entre 000...₃ e 22222...₃. Assim, os números restantes após o primeiro passo consistem em

Números do formulário 0.0xxxxx...₃ (incluindo 0,022222...₃ = 1/3)
Números do formulário 0.2xxxxx...₃ (incluindo 0,222222...₃ = 1)

Isso pode ser resumido dizendo que esses números com uma representação ternária, de modo que o primeiro dígito após o ponto da Radix não seja 1 sejam os que restam após a primeira etapa.

A segunda etapa remove os números do formulário 0,01xxxx... 3 e 0,21XXXX... _{3 </SUN Conclua -se que os números restantes são aqueles com um número ternário onde nenhum dos primeiros dois dígitos é 1.}

Continuando dessa maneira, para que um número não seja excluído na etapa n , ele deve ter uma representação ternária cujo n th não é 1. para um número Para estar no conjunto de Cantor, ele não deve ser excluído em nenhuma etapa, deve admitir uma representação numeral que consiste inteiramente de 0s e 2s.

Vale ressaltar que números como 1, 1/3 = 0,1₃ e 7/9 = 0,21₃ estão no conjunto Cantor, como eles têm números ternários que consistem inteiramente de 0s e 2s: 1 = 0,222...₃ = 0.2₃, 1/3 = 0,0222...₃ = 0,02₃ e 7/9 - 0,20222...₃ = 0,202₃. Todos os últimos números são “pontos finais”, e estes exemplos são pontos de limite certos de ${mathcal {C}}$ . O mesmo é verdadeiro para os pontos de limite esquerdo de ${mathcal {C}}$ Por exemplo. 2/3 = 0,1222...₃ = 0,12₃ = 0,20₃ e 8/9 = 0,21222...₃ = 0,212₃ = 0,220₃. Todos estes pontos finais são ternary apropriado frações (elementos de ${displaystyle mathbb {Z} cdot 3^{-mathbb {N} _{0}}}$ ) da forma p/q, onde denominador q é um poder de 3 quando a fração está em sua forma irredutível. A representação ternary dessas frações termina (isto é, é finita) ou — lembre-se de acima que as frações ternárias adequadas cada um tem 2 representações — é infinita e “fim” em ambos infinitamente muitos 0s recorrentes ou infinitamente muitos 2s recorrentes. Tal fração é um ponto limite esquerdo de ${mathcal {C}}$ se sua representação ternary não contém 1 e “fim” em infinitamente muitos 0s recorrentes. Da mesma forma, uma fração ternary adequada é um ponto limite direito de ${mathcal {C}}$ se ele novamente sua expansão ternary não contém 1 e “fim” em infinitamente muitos 2s recorrentes.

Este conjunto de endpoints é denso em ${mathcal {C}}$ (mas não denso em [0, 1]) e constitui um conjunto contável infinito. Os números em ${mathcal {C}}$ que são não endpoints também têm apenas 0s e 2s em sua representação ternary, mas eles não podem terminar em uma repetição infinita do dígito 0, nem do dígito 2, porque então seria um endpoint.

A função de ${mathcal {C}}$ para [0,1] é definido tomando os numerais ternários que consistem inteiramente de 0s e 2s, substituindo todos os 2s por 1s, e interpretando a sequência como uma representação binária de um número real. Em uma fórmula,

{displaystyle f{bigg (}sum _{kin mathbb {N} }a_{k}3^{-k}{bigg)}=sum _{kin mathbb {N} }{frac {a_{k}}{2}}2^{-k}}

Onde?

{displaystyle forall kin mathbb {N}:a_{k}in {0,2}.}

Para qualquer número Sim. em [0,1], sua representação binária pode ser traduzida em uma representação ternary de um número x em ${mathcal {C}}$ substituindo todos os 1s por 2s. Com isto, f(x) = Sim. assim Sim. está na gama de f. Por exemplo, se Sim. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 3/5 = 0,100110011001...₂ = 0.1001, escrevemos x = 0.2002 = 0.2002200220022002...₃ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 7/10.. Consequentemente, f é subjetivo. No entanto, f o não injecção — valores para os quais f(x) coincidem aqueles em fins opostos de um dos terços médios removido. Por exemplo, tome

13 = 0,02₃ (que é um ponto limite direito de

{mathcal {C}}

e um ponto limite esquerdo do terceiro meio [13, 23) e

23 = 0,20₃ (que é um ponto limite esquerdo de

{mathcal {C}}

e um ponto limite direito do terceiro meio [13, 23]

Então

{displaystyle {begin{array}{lcl}f{bigl (}{}^{1}!!/!_{3}{bigr)}=f(0.0{overline {2}}_{3})=0.0{overline {1}}_{2}=!!&!!0.1_{2}!!&!!=0.1{overline {0}}_{2}=f(0.2{overline {0}}_{3})=f{bigl (}{}^{2}!!/!_{3}{bigr)}.\&parallel \&{}^{1}!!/!_{2}end{array}}}

Assim, há tantos pontos no conjunto Cantor como há no intervalo [0, 1] (que tem a cardinalidade incontável ${displaystyle {mathfrak {c}}=2^{aleph _{0}}}$ ). No entanto, o conjunto de endpoints dos intervalos removidos é contável, então deve haver incontavelmente muitos números no conjunto Cantor que não são pontos finais de intervalo. Como observado acima, um exemplo de tal número é 1/4, que pode ser escrito como 0,020202...₃ = 0.02 em notação ternary. Na verdade, dado qualquer ${displaystyle ain [-1,1]}$ , existe ${displaystyle x,yin {mathcal {C}}}$ tal que ${displaystyle a=y-x}$ . Isto foi demonstrado pela primeira vez por Steinhaus em 1917, que provou, através de um argumento geométrico, a afirmação equivalente de que ${displaystyle {(x,y)in mathbb {R} ^{2}mid y=x+a};cap ;({mathcal {C}}times {mathcal {C}})neq emptyset }$ para todos ${displaystyle ain [-1,1]}$ . Uma vez que esta construção fornece uma injeção de $[-1,1]$ para ${displaystyle {mathcal {C}}times {mathcal {C}}}$ nós temos ${displaystyle |{mathcal {C}}times {mathcal {C}}|geq |[-1,1]|={mathfrak {c}}}$ como uma coroação imediata. Assumindo que ${displaystyle |Atimes A|=|A|}$ para qualquer conjunto infinito $A$ (uma declaração que mostra ser equivalente ao axioma da escolha por Tarski), isso fornece outra demonstração de que ${displaystyle |{mathcal {C}}|={mathfrak {c}}}$ .

O conjunto de Cantor contém tantos pontos quanto o intervalo do qual é obtido, mas ele próprio não contém nenhum intervalo de comprimento diferente de zero. Os números irracionais têm a mesma propriedade, mas o conjunto de Cantor tem a propriedade adicional de ser fechado, por isso não é nem denso em nenhum intervalo, ao contrário dos números irracionais que são densos em todos os intervalos.

Conjecturou-se que todos os números irracionais algébricos são normais. Como os membros do conjunto de Cantor não são normais, isso implicaria que todos os membros do conjunto de Cantor são racionais ou transcendentais.

Auto-semelhança

O conjunto Cantor é o protótipo de um fractal. É auto-similar, porque é igual a duas cópias de si mesmo, se cada cópia é encolhida por um fator de 3 e traduzida. Mais precisamente, o conjunto Cantor é igual à união de duas funções, as transformações de auto-similaridade esquerda e direita de si mesmo, ${displaystyle T_{L}(x)=x/3}$ e ${displaystyle T_{R}(x)=(2+x)/3}$ , que deixam o Cantor invariante até ao homeomorfismo: ${displaystyle T_{L}({mathcal {C}})cong T_{R}({mathcal {C}})cong {mathcal {C}}=T_{L}({mathcal {C}})cup T_{R}({mathcal {C}}).}$

Iteração repetida de $T_{L}$ e $T_{R}$ pode ser visualizado como uma árvore binária infinita. Ou seja, em cada nó da árvore, pode-se considerar o subárvore à esquerda ou à direita. Tomando o conjunto ${displaystyle {T_{L},T_{R}}}$ juntamente com a composição da função forma um monoide, o monóide dídico.

Os automorfismos da árvore binária são suas rotações hiperbólicas, e são dadas pelo grupo modular. Assim, o conjunto Cantor é um espaço homogêneo no sentido de que para qualquer dois pontos $x$ e $y$ no conjunto Cantor ${mathcal {C}}$ existe um homeomorfismo ${displaystyle h:{mathcal {C}}to {mathcal {C}}}$ com $h(x)=y$ . Uma construção explícita $h$ pode ser descrito mais facilmente se vermos o conjunto Cantor como um espaço de produto de muitas cópias contáveis do espaço discreto ${0,1}$ . Então o mapa ${displaystyle h:{0,1}^{mathbb {N} }to {0,1}^{mathbb {N} }}$ definido por ${displaystyle h_{n}(u):=u_{n}+x_{n}+y_{n}mod 2}$ é um homeomorfismo involutivo que troca $x$ e $y$ .

Lei de conservação

Descobriu-se que alguma forma de lei de conservação é sempre responsável por escalonamento e auto-similaridade. No caso do conjunto Cantor pode ser visto que o $d_{f}$ o momento (onde ${displaystyle d_{f}=ln(2)/ln(3)}$ é a dimensão fractal) de todos os intervalos sobreviventes em qualquer fase do processo de construção é igual a constante que é igual a um no caso do conjunto Cantor. Sabemos que há $N=2^n$ intervalos de tamanho ${displaystyle 1/3^{n}}$ presente no sistema no $n$ o passo de sua construção. Então, se rotularmos os intervalos sobreviventes como ${displaystyle x_{1},x_{2},ldotsx_{2^{n}}}$ então o $d_{f}$ o momento é ${displaystyle x_{1}^{d_{f}}+x_{2}^{d_{f}}+cdots +x_{2^{n}}^{d_{f}}=1}$ desde então ${displaystyle x_{1}=x_{2}=cdots =x_{2^{n}}=1/3^{n}}$ .

A dimensão de Hausdorff do conjunto de Cantor é igual a ln(2)/ln(3) ≈ 0,631.

Propriedades topológicas e analíticas

Embora "o" O conjunto de Cantor normalmente se refere ao conjunto de Cantor de terços médios original descrito acima, os topologistas costumam falar sobre "a" Conjunto de Cantor, que significa qualquer espaço topológico que seja homeomorfo (topologicamente equivalente) a ele.

Como mostra o argumento de soma acima, o conjunto de Cantor é incontável, mas tem medida de Lebesgue 0. Como o conjunto de Cantor é o complemento de uma união de conjuntos abertos, ele próprio é um subconjunto fechado dos reais e, portanto, uma métrica completa espaço. Como também é totalmente limitado, o teorema de Heine-Borel diz que deve ser compacto.

Para qualquer ponto no conjunto de Cantor e qualquer vizinhança arbitrariamente pequena do ponto, existe algum outro número com um numeral ternário de apenas 0s e 2s, bem como números cujos numerais ternários contêm 1s. Portanto, todo ponto no conjunto de Cantor é um ponto de acumulação (também chamado de ponto de agrupamento ou ponto limite) do conjunto de Cantor, mas nenhum é um ponto interior. Um conjunto fechado no qual todo ponto é um ponto de acumulação também é chamado de conjunto perfeito em topologia, enquanto um subconjunto fechado do intervalo sem pontos interiores não é denso em nenhum lugar do intervalo.

Cada ponto do conjunto de Cantor também é um ponto de acumulação do complemento do conjunto de Cantor.

Para quaisquer dois pontos no conjunto de Cantor, haverá algum dígito ternário onde eles diferem — um terá 0 e o outro 2. Ao dividir o conjunto de Cantor em "metades" dependendo do valor deste dígito, obtém-se uma partição do conjunto de Cantor em dois conjuntos fechados que separam os dois pontos originais. Na topologia relativa do conjunto de Cantor, os pontos foram separados por um conjunto clopen. Consequentemente, o conjunto de Cantor é totalmente desconectado. Como um espaço Hausdorff compacto totalmente desconectado, o conjunto Cantor é um exemplo de espaço Stone.

Como um espaço topológico, o conjunto Cantor é naturalmente homeomorphic ao produto de muitas cópias contáveis do espaço ${0,1}$ , onde cada cópia carrega a topologia discreta. Este é o espaço de todas as sequências em dois dígitos

{displaystyle 2^{mathbb {N} }={(x_{n})mid x_{n}in {0,1}{text{ for }}nin mathbb {N} },}

que também pode ser identificado com o conjunto de números inteiros 2-adic. A base para os conjuntos abertos da topologia do produto são conjuntos de cilindros; O homeomorfismo os mapeia para a topologia do subespaço que o Cantor estabelece herda da topologia natural na linha real. Essa caracterização do espaço Cantor como produto de espaços compactos fornece uma segunda prova de que o espaço de Cantor é compacto, através do teorema de Tychonoff.

A partir da caracterização acima, o conjunto de Cantor é homeomórfico para os números inteiros p-adic e, se um ponto for removido dele, para os números p-adic.

O conjunto Cantor é um subconjunto dos reais, que são um espaço métrico em relação à métrica de distância comum; portanto, o conjunto Cantor é um espaço métrico, usando essa mesma métrica. Alternativamente, pode-se usar a métrica p-ádica em $2^mathbb{N}$ : dado duas sequências $(x_n),(y_n)in 2^mathbb{N}$ , a distância entre eles é ${displaystyle d((x_{n}),(y_{n}))=2^{-k}}$ , onde $k$ é o menor índice tal que $x_k ne y_k$ ; se não houver tal índice, então as duas sequências são as mesmas, e uma define a distância a ser zero. Estas duas métricas geram a mesma topologia no conjunto Cantor.

Vimos acima que o conjunto de Cantor é um espaço métrico compacto perfeito totalmente desconectado. De fato, em certo sentido, é o único: todo espaço métrico compacto perfeito não vazio totalmente desconectado é homeomorfo ao conjunto de Cantor. Consulte Espaço de Cantor para saber mais sobre espaços homeomórficos ao conjunto de Cantor.

O conjunto de Cantor às vezes é considerado "universal" na categoria de espaços métricos compactos, pois todo espaço métrico compacto é uma imagem contínua do conjunto de Cantor; no entanto, esta construção não é única e, portanto, o conjunto de Cantor não é universal no sentido categórico preciso. O "universal" A propriedade tem aplicações importantes na análise funcional, onde às vezes é conhecida como o teorema de representação para espaços métricos compactos.

Para qualquer inteiro q ≥ 2, a topologia no grupo G = Z_q^ω (a soma direta contável) é discreta. Embora o Pontrjagin dual Γ também seja Z_q^ω, a topologia de Γ é compacta. Pode-se ver que Γ é totalmente desconectado e perfeito - portanto, é homeomorfo ao conjunto de Cantor. É mais fácil escrever o homeomorfismo explicitamente no caso q = 2. (Veja Rudin 1962 p 40.)

A média geométrica do conjunto de Cantor é aproximadamente 0,274974.

Medida e probabilidade

O conjunto de Cantor pode ser visto como o grupo compacto de sequências binárias e, como tal, é dotado de uma medida natural de Haar. Quando normalizado para que a medida do conjunto seja 1, é um modelo de uma sequência infinita de lançamentos de moedas. Além disso, pode-se mostrar que a medida de Lebesgue usual no intervalo é uma imagem da medida de Haar no conjunto de Cantor, enquanto a injeção natural no conjunto ternário é um exemplo canônico de uma medida singular. Também pode ser mostrado que a medida de Haar é uma imagem de qualquer probabilidade, fazendo com que o Cantor defina um espaço de probabilidade universal em alguns aspectos.

Na teoria da medida de Lebesgue, o conjunto de Cantor é um exemplo de um conjunto que é incontável e tem medida zero. Em contraste, o conjunto tem uma medida Hausdorff de 1 em sua dimensão de log 2 / log 3.

Números do cantor

Se definirmos um número de Cantor como um membro do conjunto de Cantor, então

Cada número real em [0, 2] é a soma de dois números Cantor.
Entre os dois números Cantor há um número que não é um número Cantor.

Teoria do conjunto descritivo

O conjunto Cantor é um conjunto meagre (ou um conjunto de primeira categoria) como um subconjunto de [0,1] (embora não como um subconjunto de si mesmo, uma vez que é um espaço Baire). O conjunto Cantor demonstra assim que as noções de "tamanho" em termos de cardinalidade, medida e (Baire) categoria não precisam coincidir. Como o conjunto ${displaystyle mathbb {Q} cap [0,1]}$ , o conjunto Cantor ${mathcal {C}}$ é "pequeno" no sentido de que é um conjunto nulo (um conjunto de medida zero) e é um subconjunto meagre de [0,1]. No entanto, ao contrário ${displaystyle mathbb {Q} cap [0,1]}$ , que é contável e tem uma cardinalidade "pequena", $aleph _{0}$ , a cardinalidade de ${mathcal {C}}$ é o mesmo que o de [0,1], o continuum ${mathfrak {c}}$ , e é "grande" no sentido da cardinalidade. De fato, também é possível construir um subconjunto de [0,1] que é minucioso, mas de medida positiva e um subconjunto que não é definido, mas de medida zero: Tomando a união contável de conjuntos de Cantor "fat" ${displaystyle {mathcal {C}}^{(n)}}$ de medida ${displaystyle lambda =(n-1)/n}$ (veja Smith–Volterra–Cantor definido abaixo para a construção), obtemos um conjunto ${textstyle {mathcal {A}}:=bigcup _{n=1}^{infty }{mathcal {C}}^{(n)}}$ que tem uma medida positiva (igual a 1), mas é meagre em [0,1], desde cada ${displaystyle {mathcal {C}}^{(n)}}$ não é nada denso. Então considere o conjunto ${textstyle {mathcal {A}}^{mathrm {c} }=[0,1]setminus bigcup _{n=1}^{infty }{mathcal {C}}^{(n)}}$ . Desde então ${displaystyle {mathcal {A}}cup {mathcal {A}}^{mathrm {c} }=[0,1]}$ , ${displaystyle {mathcal {A}}^{mathrm {c} }}$ não pode ser meagre, mas desde ${displaystyle mu ({mathcal {A}})=1}$ , ${displaystyle {mathcal {A}}^{mathrm {c} }}$ deve ter medida zero.

Variantes

Smith - Volterra - conjunto

Em vez de remover repetidamente o terço médio de cada peça como no conjunto Cantor, também podemos continuar removendo qualquer outra porcentagem fixa (excepto 0% e 100%) do meio. No caso em que o meio 8/10. do intervalo é removido, obtemos um caso notavelmente acessível — o conjunto consiste em todos os números em [0,1] que podem ser escritos como um decimal composto inteiramente de 0s e 9s. Se uma porcentagem fixa for removida em cada etapa, então o conjunto limitante terá medida zero, uma vez que o comprimento do restante ${displaystyle (1-f)^{n}to 0}$ como $nto infty$ para qualquer $f$ tal que $<math alttext="{displaystyle 00<f\leq \leq 1{displaystyle 0<fleq 1 <img alt="{displaystyle 0$ .

Por outro lado, "fat Cantor sets" de medida positiva pode ser gerado pela remoção de frações menores do meio do segmento em cada iteração. Assim, pode-se construir conjuntos homeomorphic ao conjunto Cantor que têm medida Lebesgue positiva enquanto ainda não está em nenhum lugar denso. Se um intervalo de comprimento $r^{n}$ ( ${displaystyle rleq 1/3}$ ) é removido do meio de cada segmento no na iteração, então o comprimento total removido é ${textstyle sum _{n=1}^{infty }2^{n-1}r^{n}=r/(1-2r)}$ , e o conjunto limitante terá uma medida de Lebesgue ${displaystyle lambda =(1-3r)/(1-2r)}$ . Assim, em certo sentido, o conjunto Cantor de terços médios é um caso limitante com ${displaystyle r=1/3}$ . Se $<math alttext="{displaystyle 0<r0<R<1/3{displaystyle 0<r<1/3} <img alt="{displaystyle 0<r$ , então o restante terá uma medida positiva com $<math alttext="{displaystyle 0<lambda 0<λ λ <1{displaystyle 0<lambda] <1 <img alt="0<lambda$ . Processo ${displaystyle r=1/4}$ é conhecido como o conjunto Smith-Volterra-Cantor, que tem uma medida de Lebesgue de $1/2$ .

Conjunto de Cantores estocásticos

Pode-se modificar a construção do conjunto de Cantor dividindo aleatoriamente em vez de igualmente. Além disso, para incorporar o tempo, podemos dividir apenas um dos intervalos disponíveis em cada etapa, em vez de dividir todos os intervalos disponíveis. No caso do conjunto de Cantor triádico estocástico, o processo resultante pode ser descrito pela seguinte equação de taxa

{displaystyle {frac {partial c(x,t)}{partial t}}=-{frac {x^{2}}{2}}c(x,t)+2int _{x}^{infty }(y-x)c(y,t),dy,}

e para o conjunto diádico estocástico de Cantor

{displaystyle {{partial c(x,t)} over {partial t}}=-xc(x,t)+(1+p)int _{x}^{infty }c(y,t),dy,}

Onde? ${displaystyle c(x,t)dx}$ é o número de intervalos de tamanho entre $x$ e ${displaystyle x+dx}$ . No caso de Cantor Triádico definir a dimensão fractal é ${displaystyle 0.5616}$ que menos do que sua contraparte determinística ${displaystyle 0.6309}$ . No caso do conjunto de cantor estocástico dídica a dimensão fractal é $p$ que é mais uma vez menos do que a sua contraparte determinística ${displaystyle ln(1+p)/ln 2}$ . No caso de Stochastic dyadic Cantor definir a solução para ${displaystyle c(x,t)}$ exibe escala dinâmica como sua solução no limite de longo prazo é ${displaystyle t^{-(1+d_{f})}e^{-xt}}$ onde a dimensão fractal do conjunto de Cantor dádico estocástico ${displaystyle d_{f}=p}$ . Em qualquer caso, como conjunto de Cantor Triádico, o $d_{f}$ o momento ( ${textstyle int x^{d_{f}}c(x,t),dx={text{constant}}}$ ) do conjunto triádico estocástico e dyadic Cantor também são quantidades conservadas.

Pó de Cantor

Poeira de Cantor é uma versão multidimensional do conjunto de Cantor. Ele pode ser formado tomando um produto cartesiano finito do conjunto de Cantor consigo mesmo, tornando-o um espaço de Cantor. Como o conjunto de Cantor, o pó de Cantor tem medida zero.

Cantor cubos progressão de recursão em direção Pó de cantor

Pó de cantor (2D)

Pó de cantor (3D)

Um análogo 2D diferente do conjunto de Cantor é o tapete de Sierpinski, onde um quadrado é dividido em nove quadrados menores e o do meio é removido. Os quadrados restantes são então divididos em nove cada e o meio removido, e assim por diante ad infinitum. Um análogo 3D disso é a esponja Menger.

Comentários históricos

uma imagem da 2a iteração da poeira de Cantor em duas dimensões

uma imagem da 4a iteração da poeira de Cantor em duas dimensões

Cantor introduziu o que chamamos hoje o conjunto de ternário Cantor ${mathcal {C}}$ como um exemplo "de um ponto-set perfeito, que não está em qualquer lugar-dense em qualquer intervalo, mas pequeno". Cantor descrito ${mathcal {C}}$ em termos de expansões ternárias, como "o conjunto de todos os números reais da fórmula: ${displaystyle z=c_{1}/3+c_{2}/3^{2}+cdots +c_{nu }/3^{nu }+cdots }$ onde os coeficientes ${displaystyle c_{nu }}$ arbitrariamente tomar os dois valores 0 e 2, e a série pode consistir de um número finito ou um número infinito de elementos."

Um espaço topológico $P$ é perfeito se todos os seus pontos são pontos limite ou, equivalentemente, se coincide com o seu conjunto derivado $P'$ . Subconjuntos da linha real, como ${mathcal {C}}$ , pode ser visto como espaços topológicos sob a topologia subespacial induzida.

Cantor foi levado ao estudo de conjuntos derivados por seus resultados sobre unicidade de séries trigonométricas. Este último fez muito para colocá-lo no caminho para o desenvolvimento de uma teoria geral abstrata de conjuntos infinitos.

Benoit Mandelbrot escreveu muito sobre pó de Cantor e sua relação com fractais naturais e física estatística. Ele refletiu ainda mais sobre a natureza intrigante ou até mesmo perturbadora de tais estruturas para aqueles na comunidade de matemática e física. Na geometria Fractal da Natureza, ele descreveu como "Quando eu comecei neste tópico em 1962, todos estavam concordando que as poeiras de Cantor são pelo menos tão monstruosas quanto as curvas de Koch e Peano", e acrescentou que "todo o físico de auto-respeito foi automaticamente desligado por uma menção de Cantor, pronto para correr a um quilômetro de qualquer pessoa que afirmasse ${mathcal {C}}$ ser interessante na ciência."

Contenido relacionado

Más resultados...