Conjunto contável

Em matemática, um conjunto é contável se for finito ou se puder ser feito em correspondência um a um com o conjunto dos números naturais. Equivalentemente, um conjunto é contável se existe uma função injetiva dele nos números naturais; isto significa que cada elemento do conjunto pode ser associado a um único número natural, ou que os elementos do conjunto podem ser contados um a um, embora a contagem nunca termine devido ao número infinito de elementos.

Em termos mais técnicos, assumindo o axioma da escolha contável, um conjunto é contável se a sua cardinalidade (o número de elementos do conjunto) não for maior que a dos números naturais. Um conjunto contável que não é finito é dito contável infinito.

O conceito é atribuído a Georg Cantor, que provou a existência de conjuntos incontáveis, ou seja, conjuntos que não são enumeráveis; por exemplo, o conjunto dos números reais.

Uma nota sobre terminologia

Embora os termos "contáveis" e "contavelmente infinito" conforme definido aqui são bastante comuns, a terminologia não é universal. Um estilo alternativo usa contável para significar o que aqui é chamado de infinito contável, e no máximo contável para significar o que aqui é chamado de contável. Para evitar ambigüidade, pode-se limitar aos termos "no máximo contáveis" e "contavelmente infinito", embora com respeito à concisão este seja o pior dos dois mundos. O leitor é aconselhado a verificar a definição em uso ao encontrar o termo "contável" na literatura.

Os termos enumeráveis e enumeráveis também podem ser usados, por exemplo referindo-se a contável e contável infinito, respectivamente, mas como as definições variam, o leitor é novamente aconselhado a verificar a definição em uso.

Definição

A definição mais concisa é em termos de cardinalidade. Um conjunto SNão. S. o Contável se a sua cardinalidade |S||S|} é inferior ou igual a ? ? 0{displaystyle aleph _{0}} (aleph-null), a cardinalidade do conjunto de números naturais N= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(0,1,2,3,...... ?{displaystyle mathbb {N} ={0,1,2,3,ldots }}. Um conjunto SNão. S. o contável infinito se |S|= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? 0{displaystyle |S|=aleph _{0}}. Um conjunto é incontável se não for contável, ou seja, sua cardinalidade é maior do que ? ? 0{displaystyle aleph _{0}}; o leitor é encaminhado para Uncountable set for further discussion.

Para cada conjunto SNão. S., as seguintes proposições são equivalentes:

• SNão. S. é contável.
• Existe uma função injetiva de S para N{displaystyle mathbb {N} } }.
• SNão. S. é vazio ou existe uma função surjetiva de N{displaystyle mathbb {N} } } para SNão. S..
• Existe um mapeamento bijetivo entre SNão. S. e um subconjunto de N{displaystyle mathbb {N} } }.
• SNão. S. é finito ou contável infinito.

Da mesma forma, as seguintes proposições são equivalentes:

• SNão. S. é contável infinito.
• Há um mapeamento injetivo e subjetivo (e, portanto, bijetivo) entre SNão. S. e N{displaystyle mathbb {N} } }.
• SNão. S. tem uma correspondência única com N{displaystyle mathbb {N} } }.
• Os elementos de SNão. S. pode ser arranjado em uma sequência infinita um0,um1,um2,...... {displaystyle a_{0},a_{1},a_{2},ldots }, onde umEu...Não. a_{i}} é diferente de umJJ{displaystyle a_{j}} para Eu...≠ ≠ JJ- Sim. e cada elemento de SNão. S. está listado.

História

Em 1874, em seu primeiro artigo de teoria dos conjuntos, Cantor provou que o conjunto dos números reais é incontável, mostrando assim que nem todos os conjuntos infinitos são contáveis. Em 1878, ele usou correspondências um-para-um para definir e comparar cardinalidades. Em 1883, ele estendeu os números naturais com seus ordinais infinitos e usou conjuntos de ordinais para produzir uma infinidade de conjuntos com diferentes cardinais infinitos.

Introdução

A conjunto é uma coleção de elementos, e pode ser descrito de muitas maneiras. Uma maneira é simplesmente listar todos os seus elementos; por exemplo, o conjunto que consiste nos inteiros 3, 4 e 5 pode ser denotado {3, 4, 5}, chamado forma de lista. Isso só é eficaz para pequenos conjuntos, no entanto; para conjuntos maiores, isso seria demorado e propenso a erros. Em vez de listar cada elemento, às vezes um ellipsis ("...") é usado para representar muitos elementos entre o elemento inicial e o elemento final em um conjunto, se o escritor acredita que o leitor pode facilmente adivinhar o que... representa; por exemplo, {1, 2, 3,..., 100} presumivelmente denota o conjunto de inteiros de 1 a 100. Mesmo neste caso, no entanto, ainda é possível para listar todos os elementos, porque o número de elementos no conjunto é finito. Se nós numeramos os elementos do conjunto 1,2, e assim por diante, até nNão., isso nos dá a definição usual de "conjuntos de tamanho nNão.".

Mapeamento bijetivo de inteiro para números pares

Alguns conjuntos são infinito infinito; estes conjuntos têm mais do que nNão. elementos onde nNão. é qualquer inteiro que pode ser especificado. (Não importa quão grande o inteiro especificado nNão. é, como n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =10.1000{displaystyle n=10^{1000}}, conjuntos infinitos têm mais do que nNão. elementos.) Por exemplo, o conjunto de números naturais, denotáveis por {0, 1, 2, 3, 4, 5,...}, tem infinitamente muitos elementos, e não podemos usar nenhum número natural para dar seu tamanho. Pode parecer natural dividir os conjuntos em diferentes classes: colocar todos os conjuntos contendo um elemento juntos; todos os conjuntos contendo dois elementos juntos;...; finalmente, montar todos os conjuntos infinitos e considerá-los como tendo o mesmo tamanho. Esta visão funciona bem para conjuntos contáveis infinitos e foi a suposição predominante antes do trabalho de Georg Cantor. Por exemplo, existem infinitamente muitos inteiros ímpares, infinitamente muitos até inteiros, e também infinitamente muitos inteiros em geral. Podemos considerar todos esses conjuntos para ter o mesmo "tamanho" porque podemos arranjar coisas tais que, para cada inteiro, há um inteiro distinto mesmo:

...... - Sim. - Sim. 2→ → - Sim. - Sim. 4,- Sim. - Sim. 1→ → - Sim. - Sim. 2,0→ → 0,1→ → 2,2→ → 4⋯ ⋯ {displaystyle ldots ,-!2!rightarrow !-!4,,-!1!rightarrow !-!2,,0!rightarrow !0,,1! !2,,2!rightarrow !4,cdots }

n→ → 2n- Sim.

? ? 0{displaystyle aleph _{0}}

Georg Cantor mostrou que nem todos os conjuntos infinitos são infinitos contáveis. Por exemplo, os números reais não podem ser colocados em correspondência de um para um com os números naturais (inteiros não negativos). O conjunto dos números reais tem uma cardinalidade maior do que o conjunto dos números naturais e é chamado de incontável.

Visão geral formal

Por definição, um conjunto SNão. S. o Contável se existe uma bijeção entre SNão. S. e um subconjunto dos números naturais N= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(0,1,2,...... ?{displaystyle mathbb {N} ={0,1,2,dots }}. Por exemplo, defina a correspondência

Desde cada elemento S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(um,b),c?Não. S={a,b,c}} é emparelhado com precisamente um elemento de (1,2,3?{displaystyle {1,2,3}}, e vice-versa, isso define uma bijeção, e mostra que SNão. S. é contável. Da mesma forma, podemos mostrar que todos os conjuntos finitos são contáveis.

Quanto ao caso de conjuntos infinitos, um conjunto SNão. S. é contável infinito se houver uma bijeção entre SNão. S. e todos N{displaystyle mathbb {N} } }. Como exemplos, considere os conjuntos A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(1,2,3,...... ?Não. A={1,2,3,dots }}, o conjunto de inteiros positivos, e B= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(0,2,4,6,...... ?Não. B={0,2,4,6,dots }}, o conjunto de inteiros pares. Podemos mostrar que esses conjuntos são contáveis infinitos exibindo uma bijeção aos números naturais. Isso pode ser alcançado usando as atribuições n ↔ Não. e n Legislação 2n, para que

Todo conjunto infinito contável é contável, e todo conjunto infinito contável é infinito contável. Além disso, qualquer subconjunto dos números naturais é contável e, de forma mais geral:

O conjunto de todos os pares ordenados de números naturais (o produto cartesiano de dois conjuntos de números naturais, N× × N{displaystyle mathbb {N} times mathbb Não. é contável infinito, como pode ser visto seguindo um caminho como o um na imagem:

A função de emparelhamento Cantor atribui um número natural a cada par de números naturais

O mapeamento resultante procede da seguinte forma:

Este mapeamento abrange todos esses pares ordenados.

Esta forma de mapeamento triangular recursivamente generaliza-se para nNão.- tuplas de números naturais, ou seja, (um1,um2,um3,...... ,umn)(a_{1},a_{2},a_{3},dotsa_{n})} Onde? umEu...Não. a_{i}} e nNão. são números naturais, mapeando repetidamente os dois primeiros elementos de um nNão.-tuple a um número natural. Por exemplo, (0, 2, 3) pode ser escrito como ((0, 2), 3). Então (0, 2) mapas a 5 assim ((0, 2), 3) mapas a (5, 3), então (5, 3) mapas a 39. Desde um diferente 2-tuple, que é um par como (um, b)), mapas para um número natural diferente, uma diferença entre dois n-tuples por um único elemento é suficiente para garantir que os n-tuples sejam mapeados para diferentes números naturais. Então, uma injeção do conjunto de nNão.-tuples para o conjunto de números naturais N{displaystyle mathbb {N} } } é provado. Para o conjunto de nNão.- tuplas feitas pelo produto cartesiano de finito muitos conjuntos diferentes, cada elemento em cada tupla tem a correspondência de um número natural, então cada tupla pode ser escrita em números naturais, então a mesma lógica é aplicada para provar o teorema.

O conjunto de todos os inteiros Z.{displaystyle mathbb {Z} } } e o conjunto de todos os números racionais Q{displaystyle mathbb {Q} } } pode intuitivamente parecer muito maior do que N{displaystyle mathbb {N} } }. Mas a aparência pode ser enganosa. Se um par é tratado como o numerador e denominador de uma fração vulgar (uma fração na forma de um/b)- Sim. Onde? umNão. e b)≠ ≠ 0{displaystyle bneq 0 são inteiros), então para cada fração positiva, podemos chegar com um número natural distinto correspondente a ele. Esta representação também inclui os números naturais, desde cada número natural nNão. é também uma fração n/1Não.. Assim, podemos concluir que existem exatamente tantos números racionais positivos como há inteiros positivos. Isso também é verdade para todos os números racionais, como pode ser visto abaixo.

De maneira semelhante, o conjunto dos números algébricos é contável.

Às vezes mais do que um mapeamento é útil: um conjunto ANão. A. ser mostrado como contável é um a um mapeado (injeção) para outro conjunto BNão., então ANão. A. é provado como confiável se BNão. é um a um mapeado para o conjunto de números naturais. Por exemplo, o conjunto de números racionais positivos pode facilmente ser mapeado para o conjunto de pares de números naturais (2-tuples) porque p/q- Sim. mapas para (p,q)(p,q)}. Uma vez que o conjunto de pares de números naturais é um a um mapeado (na verdade uma a uma correspondência ou bijeção) para o conjunto de números naturais como mostrado acima, o conjunto de números racionais positivos é provado como contável.

Com a previsão de saber que existem conjuntos incontáveis, podemos nos perguntar se esse último resultado pode ou não ser levado adiante. A resposta é "sim" e "não", podemos estendê-lo, mas precisamos assumir um novo axioma para fazê-lo.

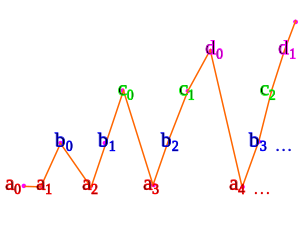
Por exemplo, dados conjuntos contáveis um,b),c,...... {displaystyle {textbf {a}},{textbf {b}},{textbf {c}},dots }

Enumeração para número contável de conjuntos contáveis

Usando uma variante da enumeração triangular que vimos acima:

• um₀ mapas para 0
• um₁ mapas para 1
• b)₀ mapas para 2
• um₂ mapas para 3
• b)₁ mapas para 4
• c₀ mapas para 5
• um₃ mapas para 6
• b)₂ mapas para 7
• c₁ mapas para 8
• D₀ mapas para 9
• um₄ mapas a 10
• ...

Isso só funciona se os conjuntos um,b),c,...... {displaystyle {textbf {a}},{textbf {b}},{textbf {c}},dots } são disjuntos. Se não, então a união é ainda menor e, portanto, também é contável por um teorema anterior.

Precisamos do axioma da escolha contável para indexar Todos os conjuntos um,b),c,...... {displaystyle {textbf {a}},{textbf {b}},{textbf {c}},dots } simultaneamente.

Este conjunto é a união das sequências de comprimento 1, as sequências de comprimento 2 e as sequências de comprimento 3, cada uma das quais é um conjunto contável (produto cartesiano finito). Portanto, estamos falando de uma união contável de conjuntos contáveis, que é contável pelo teorema anterior.

Os elementos de qualquer subconjunto finito podem ser ordenados em uma sequência finita. Existem apenas muitas sequências finitas contáveis, portanto também existem apenas muitos subconjuntos finitos contáveis.

Isso segue das definições de conjunto contável como funções injetivas/sobrejetivas.

Teorema de Cantor afirma que se ANão. A. é um conjunto e P(A){displaystyle {mathcal {P}}(A)} é seu conjunto de energia, ou seja, o conjunto de todos os subconjuntos de ANão. A., então não há função surjetiva de ANão. A. para P(A){displaystyle {mathcal {P}}(A)}. Uma prova é dada no teorema do artigo Cantor. Como consequência imediata deste e do teorema Básico acima temos:

Para uma elaboração desse resultado, consulte o argumento diagonal de Cantor.

O conjunto de números reais é incontável, assim como o conjunto de todas as seqüências infinitas de números naturais.

O modelo mínimo da teoria dos conjuntos é contável

Se houver um conjunto que seja um modelo padrão (consulte o modelo interno) da teoria do conjunto de ZFC, existe um modelo padrão mínimo (consulte o universo construtível). O teorema de Löwenheim -Skolem pode ser usado para mostrar que esse modelo mínimo é contável. O fato de que a noção de incontabilidade " Faz sentido mesmo neste modelo e, em particular, que esse modelo M contém elementos que são:

• subconjuntos de M, portanto contável,
• mas incontável do ponto de vista de M,

foi visto como paradoxal nos primeiros dias da teoria dos conjuntos, consulte o paradoxo de Skolem para mais.

O modelo padrão mínimo inclui todos os números algébricos e todos os números transcendentais efetivamente computáveis, além de muitos outros tipos de números.

Ordens totais

Conjuntos contáveis podem ser totalmente ordenados de várias maneiras, por exemplo:

• Bem-ordens (veja também o número ordinal):
  • A ordem habitual de números naturais (0, 1, 2, 3, 4, 5,...)
  • Os inteiros na ordem (0, 1, 2, 3,...; −1, −2, −3,...)
• Outros (não boas ordens:
  • A ordem usual de inteiros (..., −3, −2, −1, 0, 1, 2, 3,...)
  • A ordem usual de números racionais (Não pode ser explicitamente escrito como uma lista ordenada!)

Em ambos os exemplos de ordens de poço aqui, qualquer subconjunto tem um menos elemento; e em ambos os exemplos de ordens não-poços, alguns subconjuntos não têm um menor elemento. Esta é a definição chave que determina se um pedido total também é um pedido de poço.