Cifra de bloco
Na criptografia, uma cifra de bloco é um algoritmo determinístico que opera em grupos de bits de tamanho fixo, chamados blocos. As cifras de bloco são componentes elementares especificados no projeto de muitos protocolos criptográficos e são amplamente utilizadas para criptografar grandes quantidades de dados, inclusive em protocolos de troca de dados. Uma cifra de bloco usa blocos como uma transformação invariável.
Mesmo uma cifra de bloco segura é adequada para a criptografia de apenas um único bloco de dados por vez, usando uma chave fixa. Uma infinidade de modos de operação foi projetada para permitir seu uso repetido de maneira segura para atingir os objetivos de segurança de confidencialidade e autenticidade. No entanto, cifras de bloco também podem aparecer como blocos de construção em outros protocolos criptográficos, como funções hash universais e geradores de números pseudo-aleatórios.
Definição
Uma cifra de bloco consiste em dois algoritmos emparelhados, um para criptografia, E, e outro para descriptografia, D. Ambos os algoritmos aceitam duas entradas: um bloco de entrada de tamanho n bits e uma chave de tamanho k bits; e ambos produzem um bloco de saída n-bit. O algoritmo de descriptografia D é definido como a função inversa da criptografia, ou seja, D = E-1. Mais formalmente, uma cifra de bloco é especificada por uma função de criptografia
- EKK(P)?E(KK,P):(0,1?k× × (0,1?n→ → (0,1?n,(P):=E(K,P):{0,1}^{k}times {0,1}^{n}rightarrow {0,1}^{n},}
que recebe como entrada uma chave K, de tamanho de bit k (chamada de chave size) e uma cadeia de bits P, de comprimento n (chamada de tamanho do bloco) e retorna uma string C de n bits. P é chamado de texto simples e C é chamado de texto cifrado. Para cada K, a função EK(P) é necessário para ser um mapeamento invertível em {0,1}n. O inverso para E é definido como uma função
- EKK- Sim. - Sim. 1(C)?DKK(C)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =D(KK,C):(0,1?k× × (0,1?n→ → (0,1?n,Não. E_{K}^{-1}(C):=D_{K}(C)=D(K,C):{0,1}^{k}times {0,1}^{n}rightarrow {0,1}^{n},}
pegando uma chave K e um texto cifrado C para retornar um valor de texto simples P, tal que
- Gerenciamento de contas Gerenciamento de contas P:DKK(EKK(P))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =P.{displaystyle forall P:D_{K}(E_{K}(P))= P.
Por exemplo, um algoritmo de criptografia de cifra de bloco pode receber um bloco de texto simples de 128 bits como entrada e gerar um bloco de texto cifrado de 128 bits correspondente. A transformação exata é controlada usando uma segunda entrada - a chave secreta. A descriptografia é semelhante: o algoritmo de descriptografia pega, neste exemplo, um bloco de 128 bits de texto cifrado junto com a chave secreta e produz o bloco original de 128 bits de texto simples.
Para cada chave KK, EKK é uma permutação (um mapeamento bijetivo) sobre o conjunto de blocos de entrada. Cada chave seleciona uma permutação do conjunto de (2n)!- Sim. possíveis permutações.
História
O design moderno das cifras de bloco é baseado no conceito de uma cifra de produto iterada. Em sua publicação seminal de 1949, Communication Theory of Secrecy Systems, Claude Shannon analisou as cifras de produto e as sugeriu como um meio de melhorar efetivamente a segurança, combinando operações simples, como substituições e permutações. As cifras de produto iteradas realizam a criptografia em várias rodadas, cada uma das quais usa uma subchave diferente derivada da chave original. Uma implementação generalizada de tais cifras denominada rede Feistel em homenagem a Horst Feistel é notavelmente implementada na cifra DES. Muitas outras realizações de cifras de bloco, como o AES, são classificadas como redes de substituição-permutação.
A raiz de todos os formatos de blocos criptográficos usados no padrão de segurança de dados da indústria de cartões de pagamento (PCI DSS) e nos padrões do American National Standards Institute (ANSI) está no Atalla Key Block (AKB), que foi uma inovação importante do Atalla Box, o primeiro módulo de segurança de hardware (HSM). Foi desenvolvido em 1972 por Mohamed M. Atalla, fundador da Atalla Corporation (agora Utimaco Atalla), e lançado em 1973. O AKB era um bloco de chaves, necessário para trocar com segurança chaves simétricas ou PINs com outros agentes do setor bancário.. Essa troca segura é realizada usando o formato AKB. A Atalla Box protegeu mais de 90% de todas as redes ATM em operação desde 1998, e os produtos Atalla ainda protegem a maioria das transações ATM do mundo desde 2014.
A publicação da cifra DES pelo United States National Bureau of Standards (posteriormente o U.S. National Institute of Standards and Technology, NIST) em 1977 foi fundamental para a compreensão pública do design moderno de cifras de bloco. Também influenciou o desenvolvimento acadêmico dos ataques criptoanalíticos. Tanto a criptoanálise diferencial quanto a linear surgiram de estudos sobre o design do DES. A partir de 2016, existe uma paleta de técnicas de ataque contra as quais uma cifra de bloco deve ser segura, além de ser robusta contra ataques de força bruta.
Design
Cifras de bloco iteradas
A maioria dos algoritmos de cifra de bloco são classificados como cifras de bloco iteradas, o que significa que eles transformam blocos de tamanho fixo de texto simples em blocos de tamanho idêntico de texto cifrado, por meio da aplicação repetida de uma transformação invertível conhecida como função round, com cada iteração referida como um round.
Normalmente, a função de rodada R usa diferentes teclas de rodada Ki como uma segunda entrada, que é derivado da chave original:
- MEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =RKKEu...(MEu...- Sim. - Sim. 1)Não. M_{i}=R_{K_{i}}(M_{i-1})}
Onde? M0Não. M_{0}} é o texto simples e MRNão. M_{r}} o cifratexto, com R ser o número de rodadas.
Frequentemente, o branqueamento de teclas é usado além disso. No início e no final, os dados são modificados com material de chave (muitas vezes com XOR, mas operações aritméticas simples como adição e subtração também são usadas):
- M0= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =M⊕ ⊕ KK0Não. M_{0}=Moplus K_{0}}
- MEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =RKKEu...(MEu...- Sim. - Sim. 1);Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1...... RNão. M_{i}=R_{K_{i}}(M_{i-1});;i=1dots r}
- C= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =MR⊕ ⊕ KKR+1Não. C=M_{r}oplus K_{r+1}}
Dado um dos esquemas de design de cifra de bloco iterados padrão, é bastante fácil construir uma cifra de bloco criptograficamente segura, simplesmente usando um grande número de rodadas. No entanto, isso tornará a cifra ineficiente. Assim, a eficiência é o critério de projeto adicional mais importante para cifras profissionais. Além disso, uma boa cifra de bloco é projetada para evitar ataques de canal lateral, como previsão de ramificação e acessos à memória dependentes de entrada que podem vazar dados secretos por meio do estado do cache ou do tempo de execução. Além disso, a cifra deve ser concisa, para pequenas implementações de hardware e software. Finalmente, a cifra deve ser facilmente criptográfica analisável, de modo que possa ser mostrado a quantos ciclos a cifra precisa ser reduzida para que os ataques criptográficos existentes funcionem – e, inversamente, que possa ser mostrado que o número de rodadas reais é grande o suficiente para proteger contra eles.
Redes de substituição-permutação
Um tipo importante de cifra de bloco iterado conhecido como rede de substituição-permutação (SPN) usa um bloco de texto simples e a chave como entradas e aplica várias rodadas alternadas que consistem em um estágio de substituição seguido por um estágio de permutação - para produzir cada bloco de saída de texto cifrado. O estágio de substituição não linear mistura os bits-chave com os do texto simples, criando a confusão de Shannon. O estágio de permutação linear então dissipa as redundâncias, criando difusão.
Uma caixa de substituição (S-box) substitui um pequeno bloco de bits de entrada por outro bloco de bits de saída. Essa substituição deve ser um-para-um, para garantir a invertibilidade (portanto, a descriptografia). Um S-box seguro terá a propriedade de que a alteração de um bit de entrada alterará cerca de metade dos bits de saída em média, exibindo o que é conhecido como efeito avalanche - ou seja, ele tem a propriedade de que cada bit de saída dependerá de cada bit de entrada.
Uma caixa de permutação (P-box) é uma permutação de todos os bits: ela pega as saídas de todas as caixas S de uma rodada, permuta os bits e os alimenta no S -caixas da próxima rodada. Um bom P-box tem a propriedade de que os bits de saída de qualquer S-box são distribuídos para tantas entradas S-box quanto possível.
A cada rodada, a chave de rodada (obtida da chave com algumas operações simples, por exemplo, usando S-boxes e P-boxes) é combinada usando alguma operação de grupo, normalmente XOR.
A descriptografia é feita simplesmente invertendo o processo (usando os inversos das caixas S e P e aplicando as chaves redondas na ordem inversa).
Cifras de Feistel
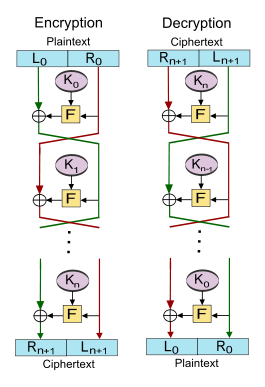
Em uma cifra de Feistel, o bloco de texto simples a ser criptografado é dividido em duas metades de tamanhos iguais. A função round é aplicada a uma metade, usando uma subchave e, em seguida, a saída é XORed com a outra metade. As duas metades são então trocadas.
Vamos. F{displaystyle rm {F}}} ser a função redonda e deixar KK0,KK1,...... ,KKnNão. K_{0},K_{1},ldots K_{n}} ser as sub-chaves para as rodadas 0,1,...... ,n{displaystyle 0,1,ldotsn} respectivamente.
Então a operação básica é a seguinte:
Dividir o bloco de texto liso em duas partes iguais, (L0{displaystyle L_{0}}, R0Não. R_{0}})
Para cada rodada Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,1,...... ,nNão., computa
- LEu...+1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =REu...Não. L_{i+1}=R_{i},}
- REu...+1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =LEu...⊕ ⊕ F(REu...,KKEu...)Não. R_{i+1}=L_{i}oplus {rm {F}}(R_{i},K_{i})}.
Então o cifratexto é (Rn+1,Ln+1)(R_{n+1},L_{n+1})}.
A descriptografia de um cifratexto (Rn+1,Ln+1)(R_{n+1},L_{n+1})} é realizado pela computação para Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =n,n- Sim. - Sim. 1,...... ,0Não. I=n,n-1,ldots0
- REu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =LEu...+1Não. R_{i}=L_{i+1},}
- LEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =REu...+1⊕ ⊕ F(LEu...+1,KKEu...)Não. L_{i}=R_{i+1}oplus {rm {F}}(L_{i+1},K_{i})}.
Então... (L0,R0)(L_{0},R_{0})} é o texto simples novamente.
Uma vantagem do modelo Feistel em comparação com uma rede de substituição-permutação é que a função redonda F{displaystyle rm {F}}} não tem que ser invertível.
Cifras Lai-Massey
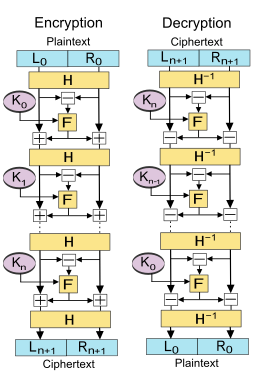
O esquema Lai-Massey oferece propriedades de segurança semelhantes às da estrutura Feistel. Ele também compartilha a vantagem de que a função redonda F{displaystyle mathrm {F} } } não tem que ser invertível. Outra semelhança é que ele também divide o bloco de entrada em duas partes iguais. No entanto, a função redonda é aplicada à diferença entre os dois, e o resultado é então adicionado a ambos os meio blocos.
Vamos. F{displaystyle mathrm {F} } } ser a função redonda e H. H. H.{displaystyle mathrm {H} } } uma função meia-redonda e deixe KK0,KK1,...... ,KKnNão. K_{0},K_{1},ldots K_{n}} ser as sub-chaves para as rodadas 0,1,...... ,n{displaystyle 0,1,ldotsn} respectivamente.
Então a operação básica é a seguinte:
Dividir o bloco de texto liso em duas partes iguais, (L0{displaystyle L_{0}}, R0Não. R_{0}})
Para cada rodada Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,1,...... ,nNão., computa
- (LEu...+1?,REu...+1?)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =H. H. H.(LEu...?+TEu...,REu...?+TEu...),(L_{i+1}',R_{i+1}')=mathrm {H} (L_{i}'+T_{i},R_{i}'+T_{i}),}
Onde? TEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =F(LEu...?- Sim. - Sim. REu...?,KKEu...)Não. T_{i}=mathrm {F} (L_{i}'-R_{i}',K_{i})} e (L0?,R0?)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =H. H. H.(L0,R0)(L_{0}',R_{0}')=mathrm {H} (L_{0},R_{0})}
Então o cifratexto é (Ln+1,Rn+1)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(Ln+1?,Rn+1?)(L_{n+1},R_{n+1})=(L_{n+1}',R_{n+1}')}.
A descriptografia de um cifratexto (Ln+1,Rn+1)(L_{n+1},R_{n+1})} é realizado pela computação para Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =n,n- Sim. - Sim. 1,...... ,0Não. I=n,n-1,ldots0
- (LEu...?,REu...?)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =H. H. H.- Sim. - Sim. 1(LEu...+1?- Sim. - Sim. TEu...,REu...+1?- Sim. - Sim. TEu...)(L_{i}',R_{i}')=mathrm {H} ^{-1}(L_{i+1}'-T_{i},R_{i+1}'-T_{i})}
Onde? TEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =F(LEu...+1?- Sim. - Sim. REu...+1?,KKEu...)Não. T_{i}=mathrm {F} (L_{i+1}'-R_{i+1}',K_{i}) ? e (Ln+1?,Rn+1?)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =H. H. H.- Sim. - Sim. 1(Ln+1,Rn+1)(L_{n+1}',R_{n+1}')=mathrm {H} ^{-1}(L_{n+1},R_{n+1})}
Então... (L0,R0)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(L0?,R0?)Não. (L_{0},R_{0})=(L_{0}',R_{0}')} é o texto simples novamente.
Operações
ARX (adicionar–girar–XOR)
Muitas cifras e hashes de bloco modernos são algoritmos ARX - sua função de rodada envolve apenas três operações: (A) adição modular, (R) rotação com quantidades fixas de rotação e (X) XOR. Exemplos incluem ChaCha20, Speck, XXTEA e BLAKE. Muitos autores desenham uma rede ARX, uma espécie de diagrama de fluxo de dados, para ilustrar essa função redonda.
Essas operações ARX são populares porque são relativamente rápidas e baratas em hardware e software, sua implementação pode ser extremamente simples e também porque são executadas em tempo constante e, portanto, são imunes a ataques de temporização. A técnica de criptoanálise rotacional tenta atacar tais funções de rodada.
Outras operações
Outras operações frequentemente usadas em cifras de bloco incluem rotações dependentes de dados como em RC5 e RC6, uma caixa de substituição implementada como uma tabela de pesquisa como no Data Encryption Standard e Advanced Encryption Standard, uma caixa de permutação e multiplicação como no IDEA.
Modos de operação
Uma cifra de bloco por si só permite a criptografia de apenas um único bloco de dados do comprimento do bloco da cifra. Para uma mensagem de comprimento variável, os dados devem primeiro ser particionados em blocos de cifra separados. No caso mais simples, conhecido como modo de livro de código eletrônico (ECB), uma mensagem é primeiro dividida em blocos separados do tamanho do bloco da cifra (possivelmente estendendo o último bloco com bits de preenchimento) e, em seguida, cada bloco é criptografado e descriptografado independentemente. No entanto, esse método ingênuo geralmente é inseguro porque blocos iguais de texto simples sempre gerarão blocos iguais de texto cifrado (para a mesma chave), de modo que os padrões na mensagem de texto simples se tornam evidentes na saída do texto cifrado.
Para superar essa limitação, vários modos de operação chamados de cifra de bloco foram projetados e especificados em recomendações nacionais como NIST 800-38A e BSI TR-02102 e padrões internacionais como ISO/IEC 10116. O conceito geral é usar a randomização dos dados de texto simples com base em um valor de entrada adicional, freqüentemente chamado de vetor de inicialização, para criar o que é chamado de criptografia probabilística. No popular modo cipher block chaining (CBC), para que a criptografia seja segura, o vetor de inicialização passado junto com a mensagem de texto simples deve ser um valor aleatório ou pseudo-aleatório, que é adicionado de maneira exclusiva ou ao primeiro bloco de texto simples antes ele é criptografado. O bloco de texto cifrado resultante é então usado como o novo vetor de inicialização para o próximo bloco de texto simples. No modo de feedback de cifra (CFB), que emula uma cifra de fluxo de auto-sincronização, o vetor de inicialização é primeiro criptografado e depois adicionado ao bloco de texto simples. O modo de feedback de saída (OFB) criptografa repetidamente o vetor de inicialização para criar um fluxo de chave para a emulação de uma cifra de fluxo síncrono. O modo contador (CTR) mais recente também cria um fluxo de chaves, mas tem a vantagem de precisar apenas de valores exclusivos e não (pseudo-)aleatórios como vetores de inicialização; a aleatoriedade necessária é derivada internamente usando o vetor de inicialização como um contador de bloco e criptografando esse contador para cada bloco.
Do ponto de vista teórico da segurança, os modos de operação devem fornecer o que é conhecido como segurança semântica. Informalmente, isso significa que, dado algum texto cifrado sob uma chave desconhecida, não se pode praticamente derivar nenhuma informação do texto cifrado (além do tamanho da mensagem) sobre o que alguém saberia sem ver o texto cifrado. Foi demonstrado que todos os modos discutidos acima, com exceção do modo ECB, fornecem essa propriedade sob os chamados ataques de texto simples escolhidos.
Preenchimento
Alguns modos, como o modo CBC, operam apenas em blocos de texto simples completos. Simplesmente estender o último bloco de uma mensagem com zero bits é insuficiente, pois não permite que um receptor distinga facilmente as mensagens que diferem apenas no número de bits de preenchimento. Mais importante, uma solução tão simples dá origem a ataques de oráculos de preenchimento muito eficientes. Um esquema de preenchimento adequado é, portanto, necessário para estender o último bloco de texto simples para o tamanho do bloco da cifra. Embora muitos esquemas populares descritos em padrões e na literatura tenham se mostrado vulneráveis a ataques de padding oracle, uma solução que adiciona um bit e depois estende o último bloco com zero bits, padronizada como "método de preenchimento 2& #34; na ISO/IEC 9797-1, provou ser seguro contra esses ataques.
Criptoanálise
Ataques de força bruta
Essa propriedade resulta na degradação da segurança da cifra de forma quadrática e precisa ser levada em consideração ao selecionar um tamanho de bloco. Há uma compensação, pois tamanhos de bloco grandes podem fazer com que o algoritmo se torne ineficiente para operar. As cifras de bloco anteriores, como o DES, normalmente selecionavam um tamanho de bloco de 64 bits, enquanto os designs mais recentes, como o AES, suportam tamanhos de bloco de 128 bits ou mais, com algumas cifras suportando uma variedade de tamanhos de bloco diferentes.
Criptoanálise diferencial
Criptoanálise linear
Uma criptoanálise linear é uma forma de criptoanálise baseada em encontrar aproximações afins para a ação de uma cifra. A análise criptográfica linear é um dos dois ataques mais amplamente usados em cifras de bloco; o outro sendo a criptoanálise diferencial.
A descoberta é atribuída a Mitsuru Matsui, que primeiro aplicou a técnica à cifra FEAL (Matsui e Yamagishi, 1992).
Criptoanálise integral
Criptoanálise integral é um ataque criptoanalítico particularmente aplicável a cifras de bloco baseadas em redes de substituição-permutação. Ao contrário da criptoanálise diferencial, que usa pares de textos claros escolhidos com uma diferença XOR fixa, a criptoanálise integral usa conjuntos ou mesmo multiconjuntos de textos claros escolhidos, dos quais parte é mantida constante e outra parte varia em todas as possibilidades. Por exemplo, um ataque pode usar 256 textos claros escolhidos que têm todos menos 8 de seus bits iguais, mas todos diferem nesses 8 bits. Tal conjunto tem necessariamente uma soma XOR igual a 0, e as somas XOR dos conjuntos correspondentes de textos cifrados fornecem informações sobre a operação da cifra. Esse contraste entre as diferenças entre pares de textos e as somas de conjuntos maiores de textos inspirou o nome "criptoanálise integral", emprestando a terminologia do cálculo.
Outras técnicas
Além da criptoanálise linear e diferencial, há um catálogo crescente de ataques: criptoanálise diferencial truncada, criptoanálise diferencial parcial, criptoanálise integral, que engloba ataques quadrados e integrais, ataques deslizantes, ataques de bumerangue, o ataque XSL, criptoanálise diferencial impossível e ataques algébricos. Para que um novo projeto de cifra de bloco tenha credibilidade, ele deve demonstrar evidências de segurança contra ataques conhecidos.
Segurança comprovável
Quando uma cifra de bloco é usada em um determinado modo de operação, o algoritmo resultante deve ser tão seguro quanto a própria cifra de bloco. ECB (discutido acima) carece enfaticamente dessa propriedade: independentemente de quão segura seja a cifra de bloco subjacente, o modo ECB pode ser facilmente atacado. Por outro lado, o modo CBC pode ser comprovado como seguro sob a suposição de que a cifra de bloco subjacente também é segura. Observe, no entanto, que fazer declarações como essa requer definições matemáticas formais para o que significa para um algoritmo de criptografia ou uma cifra de bloco "ser seguro". Esta seção descreve duas noções comuns para quais propriedades uma cifra de bloco deve ter. Cada um corresponde a um modelo matemático que pode ser usado para provar propriedades de algoritmos de nível superior, como o CBC.
Esta abordagem geral para criptografia – provando que algoritmos de nível superior (como CBC) são seguros sob suposições explicitamente declaradas em relação a seus componentes (como uma cifra de bloco) – é conhecida como segurança comprovável.
Modelo padrão
Informalmente, uma cifra de bloco é segura no modelo padrão se um invasor não conseguir distinguir entre a cifra de bloco (equipada com uma chave aleatória) e uma permutação aleatória.
Para ser um pouco mais preciso, seja E uma cifra de bloco de n bits. Imaginamos o seguinte jogo:
- A pessoa que executa o jogo vira uma moeda.
- Se a moeda cair na cabeça, ele escolhe uma chave aleatória KK e define a função f = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = EKK.
- Se a moeda cair em caudas, ele escolhe uma permutação aleatória D no conjunto de n-bit strings e define a função f = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = D.
- O atacante escolhe um n-bit string X, e a pessoa que executa o jogo diz-lhe o valor de f(X).
- Passo 2 é repetido um total de q tempos. (cada um destes q interações é um Pergunta.)
- O atacante adivinha como a moeda aterrou. Ele ganha se o seu palpite estiver correto.
O atacante, que podemos modelar como um algoritmo, é chamado de adversário. A função f (que o adversário foi capaz de consultar) é chamada de oráculo.
Observe que um adversário pode garantir trivialmente uma chance de 50% de vitória simplesmente adivinhando aleatoriamente (ou mesmo, por exemplo, sempre adivinhando "cara"). Portanto, seja PE(A) a probabilidade de o adversário A vencer este jogo contra E, e defina a vantagem de A como 2(PE (A) − 1/2). Segue-se que se A adivinhar aleatoriamente, sua vantagem será 0; por outro lado, se A sempre vence, então sua vantagem é 1. A cifra de bloco E é uma permutação pseudoaleatória (PRP) se nenhum adversário tiver uma vantagem significativamente maior que 0, dadas as restrições especificadas em q e o tempo de execução do adversário. Se no Passo 2 acima os adversários tiverem a opção de aprender f−1(X) em vez de f(X) (mas ainda tem apenas pequenas vantagens), então E é um PRP forte (SPRP). Um adversário é não adaptável se escolher todos os valores de q para X antes do início do jogo (ou seja, não usar nenhuma informação obtida das consultas anteriores para escolher cada X à medida que avança).
Estas definições provaram ser úteis para analisar vários modos de operação. Por exemplo, pode-se definir um jogo semelhante para medir a segurança de um algoritmo de criptografia baseado em cifra de bloco e, em seguida, tentar mostrar (por meio de um argumento de redução) que a probabilidade de um adversário vencer esse novo jogo não é muito maior que PE(A) para algum A. (A redução normalmente fornece limites em q e o tempo de execução de A.) De forma equivalente, se PE(A) é pequeno para todos os A relevantes, então nenhum atacante tem uma probabilidade significativa de ganhar o novo jogo. Isso formaliza a ideia de que o algoritmo de nível superior herda a segurança da cifra de bloco.
Modelo de cifra ideal
Avaliação prática
As cifras de bloco podem ser avaliadas de acordo com vários critérios na prática. Fatores comuns incluem:
- Parâmetros-chave, como o tamanho da chave e o tamanho do bloco, ambos que fornecem um limite superior na segurança da cifra.
- O nível de segurança estimado, que é baseado na confiança adquirida no projeto de cifra de bloco depois que tem resistido em grande parte grandes esforços na criptoanálise ao longo do tempo, a solidez matemática do projeto, e a existência de ataques práticos ou certificacionais.
- A cifra complexidade e sua adequação para implementação em hardware ou software. Implementações de hardware podem medir a complexidade em termos de contagem de portões ou consumo de energia, que são parâmetros importantes para dispositivos com restrições de recursos.
- A cifra desempenho em termos de processamento de produtividade em várias plataformas, incluindo seus requisitos de memória.
- O custo da cifra refere-se aos requisitos de licenciamento que podem ser aplicados devido aos direitos de propriedade intelectual.
- O flexibilidade da cifra inclui sua capacidade de suportar vários tamanhos de chaves e comprimentos de bloco.
Cifras de bloco notáveis
Lúcifer / DES
O Lúcifer é geralmente considerado a primeira cifra de bloco civil, desenvolvida na IBM na década de 1970 com base no trabalho feito por Horst Feistel. Uma versão revisada do algoritmo foi adotada como um padrão de processamento de informações federais do governo dos EUA: FIPS PUB 46 Data Encryption Standard (DES). Foi escolhido pelo National Bureau of Standards (NBS) dos EUA após um convite público para submissões e algumas mudanças internas pelo NBS (e, potencialmente, pela NSA). DES foi lançado publicamente em 1976 e tem sido amplamente utilizado.
O DES foi projetado para, entre outras coisas, resistir a um certo ataque criptanalítico conhecido pela NSA e redescoberto pela IBM, embora desconhecido publicamente até ser redescoberto novamente e publicado por Eli Biham e Adi Shamir no final dos anos 1980. A técnica é chamada de criptoanálise diferencial e continua sendo um dos poucos ataques gerais contra cifras de bloco; a criptoanálise linear é outra, mas pode ter sido desconhecida até mesmo pela NSA, antes de sua publicação por Mitsuru Matsui. O DES gerou uma grande quantidade de outros trabalhos e publicações em criptografia e criptoanálise na comunidade aberta e inspirou muitos novos designs de cifras.
DES tem um tamanho de bloco de 64 bits e um tamanho de chave de 56 bits. Blocos de 64 bits tornaram-se comuns em projetos de cifras de bloco após o DES. O comprimento da chave dependia de vários fatores, incluindo regulamentação governamental. Muitos observadores na década de 1970 comentaram que o tamanho da chave de 56 bits usado para o DES era muito curto. Com o passar do tempo, sua inadequação tornou-se aparente, especialmente depois que uma máquina especial projetada para quebrar o DES foi demonstrada em 1998 pela Electronic Frontier Foundation. Uma extensão do DES, Triple DES, criptografa cada bloco com duas chaves independentes (chave de 112 bits e segurança de 80 bits) ou três chaves independentes (chave de 168 bits e segurança de 112 bits). Foi amplamente adotado como um substituto. A partir de 2011, a versão de três chaves ainda é considerada segura, embora os padrões do Instituto Nacional de Padrões e Tecnologia (NIST) não permitam mais o uso da versão de duas chaves em novos aplicativos, devido ao seu nível de segurança de 80 bits.
IDEIA
O Algoritmo Internacional de Criptografia de Dados (IDEA) é uma cifra de bloco projetada por James Massey da ETH Zurich e Xuejia Lai; foi descrito pela primeira vez em 1991, como um substituto pretendido para o DES.
IDEA opera em blocos de 64 bits usando uma chave de 128 bits e consiste em uma série de oito transformações idênticas (uma volta) e uma transformação de saída (a meia volta eu>). Os processos de criptografia e descriptografia são semelhantes. O IDEA deriva muito de sua segurança intercalando operações de diferentes grupos – adição e multiplicação modulares e bit a bit exclusivo ou (XOR) – que são algebricamente "incompatíveis" em algum sentido.
Os projetistas analisaram o IDEA para medir sua força contra a criptoanálise diferencial e concluíram que ele é imune sob certas suposições. Nenhuma fraqueza linear ou algébrica bem-sucedida foi relatada. A partir de 2012, o melhor ataque que se aplica a todas as chaves pode quebrar uma IDEA completa de 8,5 rodadas usando um ataque de bicliques estreitos cerca de quatro vezes mais rápido que a força bruta.
RC5
RC5 é uma cifra de bloco projetada por Ronald Rivest em 1994 que, ao contrário de muitas outras cifras, tem um tamanho de bloco variável (32, 64 ou 128 bits), tamanho de chave (0 a 2040 bits) e um número de rodadas (0 a 255). A escolha original sugerida dos parâmetros era um tamanho de bloco de 64 bits, uma chave de 128 bits e 12 rodadas.
Uma característica fundamental do RC5 é o uso de rotações dependentes de dados; um dos objetivos do RC5 era estimular o estudo e avaliação dessas operações como uma primitiva criptográfica. O RC5 também consiste em várias adições modulares e XORs. A estrutura geral do algoritmo é uma rede do tipo Feistel. As rotinas de criptografia e descriptografia podem ser especificadas em algumas linhas de código. A tabela de chaves, no entanto, é mais complexa, expandindo a chave usando uma função essencialmente unidirecional com as expansões binárias de e e da proporção áurea como fontes de "nada na manga". A simplicidade tentadora do algoritmo, juntamente com a novidade das rotações dependentes de dados, tornou o RC5 um objeto de estudo atraente para criptoanalistas.
RC5 de 12 rodadas (com blocos de 64 bits) é suscetível a um ataque diferencial usando 244 textos simples escolhidos. 18–20 rodadas são sugeridas como proteção suficiente.
Rijndael / AES
A cifra Rijndael desenvolvida pelos criptógrafos belgas, Joan Daemen e Vincent Rijmen, foi um dos designs concorrentes para substituir o DES. Ele venceu o concurso público de 5 anos para se tornar o AES (Advanced Encryption Standard).
Adotado pelo NIST em 2001, o AES tem um tamanho de bloco fixo de 128 bits e um tamanho de chave de 128, 192 ou 256 bits, enquanto o Rijndael pode ser especificado com tamanhos de bloco e chave em qualquer múltiplo de 32 bits, com um mínimo de 128 bits. O tamanho do bloco tem no máximo 256 bits, mas o tamanho da chave não tem máximo teórico. O AES opera em uma matriz de bytes de ordem principal de 4 × 4 colunas, denominada estado (versões do Rijndael com um tamanho de bloco maior têm colunas adicionais no estado).
Blowfish
Blowfish é uma cifra de bloco, projetada em 1993 por Bruce Schneier e incluída em um grande número de conjuntos de cifras e produtos de criptografia. Blowfish tem um tamanho de bloco de 64 bits e um comprimento de chave variável de 1 bit até 448 bits. É uma cifra Feistel de 16 rodadas e usa grandes S-boxes dependentes de chave. As características notáveis do projeto incluem as S-boxes dependentes de chave e uma programação chave altamente complexa.
Ele foi projetado como um algoritmo de uso geral, concebido como uma alternativa ao antigo DES e livre dos problemas e restrições associados a outros algoritmos. Na época em que o Blowfish foi lançado, muitos outros designs eram proprietários, obstruídos por patentes ou eram segredos comerciais/governamentais. Schneier afirmou que "Blowfish não é patenteado e permanecerá assim em todos os países. O algoritmo é colocado em domínio público e pode ser usado livremente por qualquer pessoa." O mesmo se aplica ao Twofish, um algoritmo sucessor de Schneier.
Generalizações
Cifras de bloco ajustáveis
M. Liskov, R. Rivest e D. Wagner descreveram uma versão generalizada de cifras de bloco chamadas "tweakable" cifras de bloco. Uma cifra de bloco ajustável aceita uma segunda entrada chamada ajuste junto com sua entrada usual de texto simples ou texto cifrado. O tweak, junto com a chave, seleciona a permutação computada pela cifra. Se a alteração de ajustes for suficientemente leve (em comparação com uma operação de configuração de tecla geralmente bastante cara), alguns novos modos de operação interessantes se tornam possíveis. O artigo sobre a teoria da criptografia de disco descreve alguns desses modos.
Criptografia com preservação de formato
As cifras de bloco tradicionalmente funcionam sobre um alfabeto binário. Ou seja, tanto a entrada quanto a saída são strings binárias, consistindo de n zeros e uns. Em algumas situações, no entanto, pode-se desejar ter uma cifra de bloco que funcione sobre algum outro alfabeto; por exemplo, criptografar números de cartão de crédito de 16 dígitos de forma que o texto cifrado também seja um número de 16 dígitos pode facilitar a adição de uma camada de criptografia ao software legado. Este é um exemplo de criptografia de preservação de formato. Mais geralmente, a criptografia de preservação de formato requer uma permutação de chave em alguma linguagem finita. Isso torna os esquemas de criptografia de preservação de formato uma generalização natural de cifras de bloco (ajustáveis). Em contraste, os esquemas de criptografia tradicionais, como o CBC, não são permutações porque o mesmo texto simples pode criptografar vários textos cifrados diferentes, mesmo quando se usa uma chave fixa.
Relação com outras primitivas criptográficas
As cifras de bloco podem ser usadas para construir outras primitivas criptográficas, como as abaixo. Para que esses outros primitivos sejam criptograficamente seguros, deve-se tomar cuidado para construí-los da maneira certa.
- As cifras de fluxo podem ser construídas usando cifras de bloco. Modo OFB e modo CTR são modos de bloco que transformam uma cifra de bloco em uma cifra de fluxo.
- Funções hash criptográficas podem ser construídas usando cifras de bloco. Veja a função de compressão unidirecional para descrições de vários tais métodos. Os métodos se assemelham aos modos de cifra de bloco de operação geralmente usados para criptografia.
- Geradores de números pseudoaleatórios criptograficamente seguros (CSPRNGs) podem ser construídos usando cifras de bloco.
- Permutações pseudoaleatórias seguras de conjuntos finitos arbitrariamente dimensionados podem ser construídas com cifras de bloco; consulte Criptografia de preservação de formato.
- Uma permutação imprevisível conhecida publicamente combinada com o clareamento de chaves é suficiente para construir uma cifra de bloco -- como a cifra de single-key Even-Mansour, talvez a cifra de bloco mais simples possível comprovavelmente segura.
- Os códigos de autenticação de mensagens (MACs) são frequentemente construídos a partir de cifras de bloco. CBC-MAC, OMAC e PMAC são tais MACs.
- A criptografia autenticada também é construída a partir de cifras de bloco. Significa tanto para criptografar e MAC ao mesmo tempo. Isso é para fornecer confidencialidade e autenticação. CCM, EAX, GCM e OCB são modos de criptografia autenticados.
Assim como cifras de bloco podem ser usadas para construir funções de hash, como SHA-1 e SHA-2 são baseadas em cifras de bloco que também são usadas independentemente como SHACAL, funções de hash podem ser usadas para construir cifras de bloco. Exemplos de tais cifras de bloco são BEAR e LION.
Contenido relacionado
Apple II
União Europeia de Radiodifusão
Adrian Lamo