Brotos (jogo)
Sprouts é um jogo imparcial de papel e lápis que pode ser analisado por suas propriedades matemáticas. Foi inventado pelos matemáticos John Horton Conway e Michael S. Paterson na Universidade de Cambridge no início dos anos 1960. A configuração é ainda mais simples do que a do popular jogo Dots and Boxes, mas a jogabilidade se desenvolve de forma muito mais artística e orgânica.
Regras
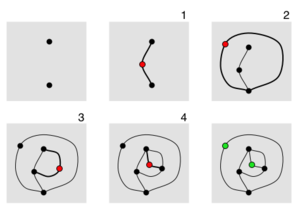
O jogo é jogado por dois jogadores, começando com alguns pontos desenhados em uma folha de papel. Os jogadores se revezam, onde cada turno consiste em traçar uma linha entre dois pontos (ou de um ponto até ele mesmo) e adicionar um novo ponto em algum lugar ao longo da linha. Os jogadores são limitados pelas seguintes regras:
- A linha pode ser reta ou curvada, mas não deve tocar ou cruzar-se ou qualquer outra linha.
- O novo ponto não pode ser colocado em cima de um dos pontos finais da nova linha. Assim, o novo ponto divide a linha em duas linhas mais curtas.
- Nenhum ponto pode ter mais de três linhas anexadas a ele. Para os propósitos desta regra, uma linha do ponto para si conta como duas linhas anexadas e novos pontos são contados como tendo duas linhas já anexadas a eles.
- Você não pode tocar um ponto duas vezes com uma linha, em seguida, conectá-lo a outra.
No chamado jogo normal, o jogador que fizer a última jogada vence. No jogo misère, o jogador que fizer o último lance perde. Misère Sprouts é talvez o único jogo combinatório misère jogado competitivamente em um fórum organizado.
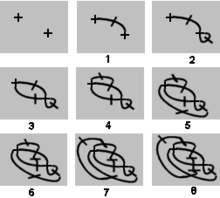
O diagrama à direita mostra um jogo de 2 pontos de Sprouts normal. Após o quarto movimento, a maioria dos pontos estão mortos – eles têm três linhas anexadas a eles, portanto não podem ser usados como pontos finais para uma nova linha. Existem dois pontos (mostrados em verde) que ainda estão vivos, com menos de três linhas anexadas. No entanto, é impossível fazer outro movimento, porque uma linha de um ponto vivo para si mesma formaria quatro ligações, e uma linha de um ponto vivo para o outro cruzaria as linhas. Portanto, nenhum quinto movimento é possível e o primeiro jogador perde. Os pontos ativos no final do jogo são chamados de sobreviventes e desempenham um papel fundamental na análise do Sprouts.
Número de movimentos
O jogo dos Sprouts sempre termina, embora esse fato não seja evidente nas regras do jogo, pois o número de vagas aumenta a cada jogada. A abordagem para entender por que o jogo sempre termina é considerar o número de vidas (oportunidades de conectar uma linha) em vez do número de pontos. Então, pode-se mostrar que se o jogo começar com n pontos, ele terminará em não mais que 3n − 1 movimentos e não menos que 2n se move.
Nas provas a seguir, presume-se que um jogo começa com n pontos e dura exatamente m movimentos.
Número máximo de movimentos
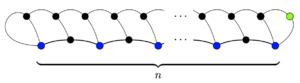
Cada local começa com três vidas e cada movimento reduz o número total de vidas no jogo em uma (duas vidas são perdidas no final da linha, mas o novo local tem uma vida). Portanto, no final do jogo, há 3n − m vidas restantes. Cada local sobrevivente tem apenas uma vida (caso contrário haveria outro movimento unindo aquele local a si mesmo), então existem exatamente 3n − m sobreviventes. Deve haver pelo menos um sobrevivente, nomeadamente a vaga adicionada no lance final. Então 3n − m ≥ 1; portanto, um jogo não pode durar mais do que 3n − 1 movimentos.
Este limite superior é na verdade o máximo e pode ser alcançado de várias maneiras, garantindo que haja apenas um sobrevivente no final do jogo. Por exemplo, o jogo à direita tem um sobrevivente e 3n − 1 movimentos.
Número mínimo de movimentos
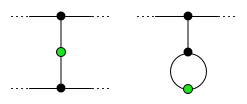
No final do jogo, um ponto morto é chamado de vizinho de um sobrevivente se for adjacente a esse sobrevivente ou, se o sobrevivente tiver um loop, for adjacente a um ponto adjacente ao sobrevivente. Isso é ilustrado no diagrama à direita. Cada sobrevivente tem exatamente dois vizinhos mortos. Nenhum ponto morto pode ser vizinho de dois sobreviventes diferentes, caso contrário haveria um movimento unindo os sobreviventes. Todos os outros pontos mortos (não vizinhos de um sobrevivente) são chamados de fariseus (do hebraico para “separados”). Suponha que existam p fariseus. Então
desde pontos iniciais + movimentos = total de pontos no final do jogo = sobreviventes + vizinhos + fariseus. Reorganizando dá:
Consequentemente, um jogo dura pelo menos 2n movimentos, e o número de fariseus é divisível por 4.
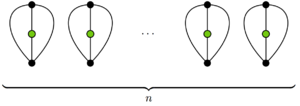
Este limite inferior para a duração de um jogo é, na verdade, o mínimo. O diagrama à direita mostra um jogo completo de 2n movimentos. Tem n sobreviventes, 2n vizinhos e 0 fariseus.
Importância em jogos reais
Os jogos reais parecem se transformar em uma batalha sobre se o número de movimentos será k ou k + 1, sendo outras possibilidades bastante improváveis. Um jogador tenta criar regiões fechadas contendo sobreviventes (reduzindo assim o número total de movimentos que serão jogados) e o outro tenta criar fariseus (aumentando assim o número de movimentos que serão jogados).
Estratégias vencedoras
Como Sprouts é um jogo finito onde nenhum empate é possível, existe uma estratégia perfeita para o primeiro ou para o segundo jogador, dependendo do número de vagas iniciais. A principal questão sobre uma determinada posição inicial é então determinar qual jogador pode forçar uma vitória se jogar perfeitamente.
Quando a estratégia vencedora é para o primeiro jogador, diz-se que o resultado da posição é uma "vitória", e quando a estratégia vencedora é para o segundo jogador, diz-se que o resultado da posição é uma "perda" (porque é uma perda do ponto de vista do primeiro jogador).
O resultado é determinado pelo desenvolvimento da árvore de jogo da posição inicial. Isto pode ser feito manualmente apenas para um pequeno número de pontos, e todos os novos resultados desde 1990 foram obtidos através de extensa pesquisa com computadores.
Versão normal
Vencendo maneiras para suas jogadas matemáticas relata que o jogo normal de 6 pontos provou ser uma vitória para o segundo jogador por Denis Mollison, com uma análise feita à mão de 47 páginas. Permaneceu como recorde por muito tempo, até a primeira análise computacional, feita na Carnegie Mellon University em 1990 por David Applegate, Guy Jacobson e Daniel Sleator. Eles alcançaram até 11 posições com alguns dos melhores hardwares disponíveis na época.
Applegate, Jacobson e Sleator observaram um padrão em seus resultados e conjecturaram que o primeiro jogador tem uma estratégia vencedora quando o número de posições dividido por seis deixa um resto de três, quatro ou cinco. Essa é uma forma matemática de dizer que o padrão apresentado pelo resultado da tabela abaixo se repete indefinidamente, com período de seis pontos.
| Pontos | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10. | 11 | ... |
| Resultado normal | Perda | Perda | Perda | Ganhar | Ganhar | Ganhar | Perda | Perda | Perda | Ganhar | Ganhar | Ganhar | ... |
Em 2001, Riccardo Focardi e Flamina Luccio descreveram um método para provar manualmente que o jogo normal de 7 pontos é uma derrota.
Então, os resultados do cálculo foram ampliados em 2006 por Josh Jordan para 14 vagas. Em 2007, Julien Lemoine e Simon Viennot introduziram um algoritmo baseado no conceito de números para acelerar a computação, atingindo até 32 pontos. Ampliaram o cômputo para 44 vagas em 2011, e três posições iniciais isoladas, com 46, 47 e 53 vagas.
Os resultados do jogo normal até agora são consistentes com as conjecturas de Applegate, Jacobson e Sleator.
Versão Misère
O histórico de computação da versão misère do Sprouts é muito semelhante ao da versão normal, com as mesmas pessoas envolvidas. Contudo, a versão misère é mais difícil de calcular e o progresso tem sido significativamente mais lento.
Em 1990, Applegate, Jacobson e Sleator alcançaram nove vagas. Com base nos seus resultados, conjecturaram que o resultado segue um padrão regular do quinto período. No entanto, esta conjectura foi invalidada em 2007, quando Josh Jordan e Roman Khorkov ampliaram a análise misère para 12 pontos: o jogo misère de 12 pontos é uma vitória, e não a derrota conjecturada. A mesma equipe alcançou 16 vagas em 2009. No mesmo ano, Julien Lemoine e Simon Viennot alcançaram 17 vagas com algoritmos complicados. Eles conseguiram estender sua análise até 20 pontos em 2011.
Conjectura-se agora que os resultados do jogo misère seguem um padrão de comprimento seis com alguns valores excepcionais: o primeiro jogador vence no misère Sprouts quando o restante (mod 6) é zero, quatro ou cinco, exceto que o primeiro jogador ganha o jogo de uma vaga e perde o jogo de quatro. A tabela abaixo mostra o padrão, com os dois valores irregulares em negrito.
| Pontos | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10. | 11 | 12 | 13 | 14 | 15 | ... |
| Resultado de Misère | Ganhar | Ganhar | Perda | Perda | Perda | Ganhar | Ganhar | Perda | Perda | Perda | Ganhar | Ganhar | Ganhar | Perda | Perda | Perda | ... |
Couves de Bruxelas
Uma variante do jogo, chamada Couve de Bruxelas em homenagem ao vegetal crucífero, começa com uma série de cruzes, ou seja, pontos com quatro pontas livres. Cada movimento envolve unir duas extremidades livres com uma curva, novamente sem cruzar nenhuma linha existente e, em seguida, colocar um traço curto na linha para criar duas novas extremidades livres. Este jogo é finito e o número total de movimentos (e, portanto, o vencedor do jogo) é predeterminado pelo número inicial de cruzamentos: os jogadores não podem afetar o resultado através do seu jogo.
Cada movimento remove duas pontas livres e introduz mais duas. Com n cruzamentos iniciais, o número de movimentos será 5n − 2, portanto, um jogo que comece com um número ímpar de cruzamentos será uma vitória do primeiro jogador, enquanto um jogo começar com um número par será a vitória do segundo jogador, independentemente dos movimentos.
Para provar isso, primeiro argumentamos que o jogo deve terminar. Então, calcularemos com precisão quantos movimentos ele precisa para terminar. Trate cada cruz como um gráfico com 5 vértices e 4 arestas. Na posição inicial com n cruzamentos, temos um grafo plano com v = 5n vértices, e = 4n arestas, f = 1 face e k = n componentes conectados. A característica de Euler para gráficos planares conectados é 2. Em um gráfico planar desconectado, obtemos
Depois de m movimentos, temos:
- e = 4n + 4m desde que em cada movimento, o jogador adiciona 4 bordas.
- v = 5n + 3m desde que em cada movimento, o jogador adiciona 3 vértices.
Então pelo acima, temos
- f - Sim. k = 1 + e - Sim. v = 1 − n + m
A seguir, observe que cada vez que adicionamos uma cruz, estamos garantindo que cada lado dessa cruz termine com um vértice de grau 1. Assim, ao longo do jogo, cada face possui pelo menos um vértice de grau 1. No entanto, o número de vértices de grau 1 é invariante ao longo do jogo e permanece em 4n. Portanto, f é no máximo 4n.
A partir disso, vemos que m = f − k − 1 + n é no máximo 5n − 2 (já que k é no mínimo 1 e f é no máximo 4n). Portanto, o jogo deve terminar, e deve terminar em no máximo 5n − 2 movimentos. Agora, argumentamos que ele deve terminar exatamente em 5n − 2 movimentos.
Na configuração final, nenhuma face pode ter mais de um vértice de grau 1, caso contrário, poderíamos conectá-los com uma cruz e ainda haveria um movimento legal. Cada face tem pelo menos um desses vértices, portanto deve terminar exatamente com um desses vértices. Portanto, na configuração final, f é exatamente 4n.
Da mesma forma, na configuração final, o grafo deve ser conectado, pois a face externa recebe pelo menos um vértice de grau 1 por componente conectado, e não pode ter mais de um desses vértices. Então, na configuração final, k é exatamente 1.
Assim, para obter a configuração final, devemos ter m = f−k−1+n = 4n−1−1+n = 5n−2.
Uma combinação de couve padrão e couve de Bruxelas também pode ser reproduzida. O jogo começa com um número arbitrário (n) de pontos ou cruzes. A cada jogada, o jogador escolhe adicionar um ponto ou uma cruz ao longo da linha que acabou de desenhar. A duração do jogo fica entre (2n) e (5n − 2), dependendo do número de pontos ou cruzes foram adicionados.
Para n = 1, começando com um ponto, o jogo terminará após 2 lances. Começando com um cruzamento, terminará após 2 lances se o primeiro jogador adicionar um ponto, após 3 lances se adicionar um cruzamento: portanto, o primeiro jogador tem uma estratégia vencedora tanto para a versão normal quanto para a versão misère. Para n > 1, a análise não está concluída.
Contenido relacionado
Pontos e caixas
Tanglóides
Antiprisma
Charles Babbage
Dodecaedro


