Árvore rubro-negra
Na ciência da computação, uma árvore vermelha-preta é uma estrutura de dados de árvore de pesquisa binária especializada, conhecida por armazenar e recuperar rapidamente informações ordenadas e por garantir que as operações serão concluídas dentro de um tempo conhecido. Em comparação com outras árvores binárias de busca com auto-equilíbrio, os nós em uma árvore vermelho-preta contêm um bit extra chamado "cor" representando "vermelho" e "preto" que é usado ao reorganizar a árvore para garantir que ela esteja sempre aproximadamente equilibrada.
Quando a árvore é modificada, a nova árvore é reorganizada e "repintada" para restaurar as propriedades de coloração que restringem o quão desequilibrada a árvore pode se tornar no pior dos casos. As propriedades são projetadas de modo que esta reorganização e recoloração possam ser realizadas de forma eficiente.
O (re-)equilíbrio não é perfeito, mas garante em busca de Big O tempo de O(log n)O(log n)}, onde nNão. é o número de entradas (ou chaves) na árvore. As operações de inserção e exclusão, juntamente com o rearranjo da árvore e recoloração, também são realizadas em O(log n)O(log n)} Hora.
Rastrear a cor de cada nó requer apenas um bit de informação por nó porque existem apenas duas cores. A árvore não contém nenhum outro dado específico por ser uma árvore vermelha e preta, portanto, seu consumo de memória é quase idêntico ao de uma árvore de pesquisa binária clássica (sem cor). Em alguns casos, a informação adicional pode ser armazenada sem custo adicional de memória.
Histórico
Em 1972, Rudolf Bayer inventou uma estrutura de dados que era um caso especial de ordem 4 de uma árvore B. Estas árvores mantiveram todos os caminhos da raiz às folhas com o mesmo número de nós, criando árvores perfeitamente equilibradas. No entanto, elas não eram árvores de pesquisa binárias. Bayer os chamou de 'árvore B binária simétrica'. em seu artigo e mais tarde eles se tornaram populares como 2–3–4 árvores ou mesmo 2–4 árvores.
Em um artigo de 1978, “A Dichromatic Framework for Balanced Trees”, Leonidas J. Guibas e Robert Sedgewick derivaram a árvore vermelha-preta da árvore B binária simétrica. A cor "vermelho" foi escolhida porque era a cor mais bonita produzida pela impressora laser colorida disponível para os autores enquanto trabalhavam na Xerox PARC. Outra resposta de Guibas afirma que foi por causa das canetas vermelhas e pretas que tinham à disposição para desenhar as árvores.
Em 1993, Arne Andersson introduziu a ideia de uma árvore inclinada para a direita para simplificar as operações de inserção e exclusão.
Em 1999, Chris Okasaki mostrou como tornar a operação de inserção puramente funcional. Sua função de equilíbrio precisava cuidar de apenas 4 casos não balanceados e um caso balanceado padrão.
O algoritmo original usou 8 casos desequilibrados, mas Cormen et al. (2001) reduziram isso para 6 casos desequilibrados. Sedgewick mostrou que a operação de inserção pode ser implementada em apenas 46 linhas de código Java. Em 2008, Sedgewick propôs a árvore vermelho-preta com inclinação para a esquerda, aproveitando a ideia de Andersson que simplificou as operações de inserção e exclusão. Sedgewick originalmente permitia nós cujos dois filhos são vermelhos, tornando suas árvores mais parecidas com 2–3–4 árvores, mas posteriormente essa restrição foi adicionada, tornando as novas árvores mais parecidas com 2–3 árvores. Sedgewick implementou o algoritmo de inserção em apenas 33 linhas, encurtando significativamente suas 46 linhas de código originais.
Terminologia
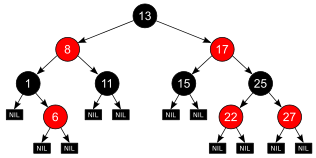
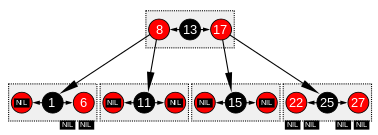
Uma árvore rubro-negra é um tipo especial de árvore de pesquisa binária, usada na ciência da computação para organizar pedaços de dados comparáveis, como fragmentos de texto ou números (como, por exemplo, os números nas figuras 1 e 2). Os nós que transportam chaves e/ou dados são frequentemente chamados de “nós internos”, mas para tornar isso muito específico, eles também são chamados de nós não NIL neste artigo.
Os nós folhas das árvores rubro-pretas ( NIL na figura 1) não contêm chaves ou dados. Essas "folhas" não precisam ser indivíduos explícitos na memória do computador: um ponteiro NULL pode —como em todas as estruturas de dados de árvore binária— codificar o fato de que não há nenhum nó filho nesta posição no nó (pai). No entanto, pela sua posição na árvore, estes objetos estão em relação a outros nós que são relevantes para a estrutura RB, podendo ter pai, irmão (ou seja, o outro filho do pai), tio, até mesmo nó sobrinho; e pode ser filho - mas nunca pai de outro nó.
Não é realmente necessário atribuir uma "cor" para esses objetos de fim de caminho, porque a condição "é NIL ou BLACK" está implícito na condição "é NIL" (veja também esta observação).
A Figura 2 mostra a mesma árvore conceitualmente vermelho-preta sem essas folhas NIL. Para chegar à mesma noção de caminho, deve-se notar que e. por exemplo, 3 caminhos passam pelo nó 1, ou seja, um caminho através de 1esquerda mais 2 caminhos adicionados através de 1direita, ou seja, os caminhos através de 6esquerda e 6direita. Dessa forma, essas extremidades dos caminhos também são pontos de encaixe para a inserção de novos nós, totalmente equivalentes às folhas NIL da figura 1.
Em vez disso, para economizar uma quantidade marginal de tempo de execução, essas (possivelmente muitas) folhas NIL podem ser implementadas como ponteiros para um nó sentinela único (e preto) (em vez de ponteiros de valor NULL).
Como conclusão, o fato de um filho não existir (não ser um nó verdadeiro, não conter dados) pode em todas as ocorrências ser especificado pelo mesmo ponteiro NULL ou como o mesmo ponteiro para um nó sentinela. Ao longo deste artigo, qualquer uma das opções é chamada de nó NIL e tem o valor constante NIL.
A profundidade negra de um nó é definida como o número de nós pretos desde a raiz até esse nó (ou seja, o número de ancestrais negros). A altura preta de uma árvore vermelho-preta é o número de nós pretos em qualquer caminho da raiz às folhas, que, pelo requisito 4, é constante (alternativamente, pode ser definido como a altura preta profundidade de qualquer nó folha). A altura preta de um nó é a altura preta da subárvore enraizada nele. Neste artigo, a altura preta de um nó NIL deve ser definida como 0, porque sua subárvore está vazia conforme sugerido pela figura 2, e a altura de sua árvore também é 0.
Propriedades
Além dos requisitos impostos a uma árvore de pesquisa binária, os seguintes requisitos devem ser satisfeitos por uma árvore vermelho-preto:
- Cada nó é vermelho ou preto.
- Todos os nós NIL (figura 1) são considerados pretos.
- Um nó vermelho não tem uma criança vermelha.
- Cada caminho de um dado nó para qualquer um de seus nós NIL descendentes passa pelo mesmo número de nós negros.
- (Conclusão) Se um nó N tem exatamente uma criança, deve ser uma criança vermelha, porque se fosse preta, seus descendentes do NIL se sentariam em uma profundidade preta diferente do que N 's criança NIL, violando a exigência 4.
Alguns autores, por ex. g. Cormen & al., afirmam que "a raiz é preta" como quinto requisito; mas não Mehlhorn & Sanders ou Sedgewick & Wayne. Como a raiz sempre pode ser alterada de vermelho para preto, esta regra tem pouco efeito na análise. Este artigo também o omite, porque perturba ligeiramente os algoritmos recursivos e as provas.
Por exemplo, toda árvore binária perfeita que consiste apenas em nós pretos é uma árvore vermelho-preta.
As operações somente leitura, como pesquisa ou travessia de árvore, não afetam nenhum dos requisitos. Em contrapartida, as operações modificadoras insert e delete mantêm facilmente os requisitos 1 e 2, mas com relação aos demais requisitos algum esforço extra deve ser feito, para evitar a introdução de uma violação do requisito 3, chamada de violação vermelha, ou do requisito 4, chamada de violação negra.
Os requisitos impõem uma propriedade crítica de árvores vermelhas-pretas: o caminho da raiz para a folha mais distante não é mais dobro do que o caminho da raiz para a folha mais próxima. O resultado é que a árvore é balanceada de altura. Uma vez que as operações tais como inserir, excluir e encontrar valores exigem pior tempo proporcional à altura hNão. da árvore, este limite superior na altura permite que as árvores vermelhas-pretas sejam eficientes no pior caso, nomeadamente logarítmica no número nNão. de entradas, i. e. h∈ ∈ O(log n){displaystyle hin O(log n)}, que não é o caso de árvores de busca binárias comuns. Para uma prova matemática ver seção Prova de limites.
Árvores vermelhas-pretas, como todas as árvores de busca binárias, permitem um acesso sequencial bastante eficiente (por exemplo, traversal em ordem, ou seja: na ordem Esquerda-Root-Right) de seus elementos. Mas eles também suportam o acesso direto assintoticamente ideal através de um traversal da raiz à folha, resultando em O(log n)O(log n)} tempo de pesquisa.
Analogia com árvores B de ordem 4
Uma árvore rubro-preta é semelhante em estrutura a uma árvore B de ordem 4, onde cada nó pode conter entre 1 e 3 valores e (consequentemente) entre 2 e 4 ponteiros filhos. Em tal árvore B, cada nó conterá apenas um valor correspondente ao valor em um nó preto da árvore rubro-negra, com um valor opcional antes e/ou depois no mesmo nó, ambos correspondendo a um nó vermelho equivalente de a árvore rubro-negra.
Uma maneira de ver essa equivalência é "subir" os nós vermelhos em uma representação gráfica da árvore vermelho-preta, de modo que eles se alinhem horizontalmente com seu nó preto pai, criando juntos um cluster horizontal. Na árvore B, ou na representação gráfica modificada da árvore rubro-negra, todos os nós folhas estão na mesma profundidade.
A árvore rubro-negra é então estruturalmente equivalente a uma árvore B de ordem 4, com fator de preenchimento mínimo de 33% dos valores por cluster e capacidade máxima de 3 valores.
Este tipo de árvore B ainda é mais geral do que uma árvore rubro-preta, pois permite ambiguidade em uma conversão de árvore rubro-preta - múltiplas árvores rubro-pretas podem ser produzidas a partir de uma árvore B equivalente de ordem 4 (veja a figura 3). Se um cluster de árvore B contiver apenas 1 valor, ele será o mínimo, preto e terá dois ponteiros filhos. Se um cluster contiver 3 valores, o valor central será preto e cada valor armazenado nas laterais será vermelho. Se o cluster contiver dois valores, entretanto, qualquer um deles poderá se tornar o nó preto na árvore vermelho-preta (e o outro será vermelho).
Portanto, a árvore B de ordem 4 não mantém qual dos valores contidos em cada cluster é a árvore negra raiz para todo o cluster e o pai dos outros valores no mesmo cluster. Apesar disso, as operações em árvores rubro-negras são mais econômicas em tempo porque não é necessário manter o vetor de valores. Pode ser caro se os valores forem armazenados diretamente em cada nó, em vez de serem armazenados por referência. Os nós da árvore B, entretanto, são mais econômicos em espaço porque você não precisa armazenar o atributo de cor para cada nó. Em vez disso, você precisa saber qual slot no vetor de cluster é usado. Se os valores forem armazenados por referência, e. g. objetos, referências nulas podem ser usadas e assim o cluster pode ser representado por um vetor contendo 3 slots para ponteiros de valor mais 4 slots para referências filhas na árvore. Nesse caso, a árvore B pode ser mais compacta em memória, melhorando a localidade dos dados.
A mesma analogia pode ser feita com árvores B com ordens maiores que podem ser estruturalmente equivalentes a uma árvore binária colorida: você só precisa de mais cores. Suponha que você adicione azul, então a árvore azul-vermelho-preta definida como árvores vermelho-pretas, mas com a restrição adicional de que dois nós sucessivos na hierarquia não serão azuis e todos os nós azuis serão filhos de um nó vermelho, então torna-se equivalente a uma árvore B cujos clusters terão no máximo 7 valores nas seguintes cores: azul, vermelho, azul, preto, azul, vermelho, azul (Para cada cluster, haverá no máximo 1 nó preto, 2 nós vermelhos e 4 nós azuis).
Para volumes moderados de valores, inserções e exclusões em uma árvore binária colorida são mais rápidas em comparação com árvores B porque as árvores coloridas não tentam maximizar o fator de preenchimento de cada cluster horizontal de nós (apenas o fator de preenchimento mínimo é garantido em árvores binárias coloridas, limitando o número de divisões ou junções de clusters). As árvores B serão mais rápidas para realizar rotações (porque as rotações ocorrerão frequentemente dentro do mesmo cluster, em vez de vários nós separados em uma árvore binária colorida). Para armazenar grandes volumes, entretanto, as árvores B serão muito mais rápidas, pois serão mais compactas ao agrupar vários filhos no mesmo cluster, onde poderão ser acessados localmente.
Todas as otimizações possíveis em árvores B para aumentar os fatores de preenchimento médios dos clusters são possíveis na árvore binária multicolorida equivalente. Notavelmente, maximizar o fator de preenchimento médio em uma árvore B estruturalmente equivalente é o mesmo que reduzir a altura total da árvore multicolorida, aumentando o número de nós não pretos. O pior caso ocorre quando todos os nós em uma árvore binária colorida são pretos, o melhor caso ocorre quando apenas um terço deles são pretos (e os outros dois terços são nós vermelhos).
Aplicativos e estruturas de dados relacionadas
Árvores rubro-negras oferecem garantias de pior caso para tempo de inserção, tempo de exclusão e tempo de pesquisa. Isto não apenas os torna valiosos em aplicações sensíveis ao tempo, como aplicações em tempo real, mas também os torna blocos de construção valiosos em outras estruturas de dados que fornecem garantias no pior caso; por exemplo, muitas estruturas de dados usadas em geometria computacional podem ser baseadas em árvores vermelho-pretas, e o Completely Fair Scheduler usado nos kernels Linux atuais e na implementação de chamadas de sistema epoll usa árvores vermelho-pretas.
A árvore AVL é outra estrutura de apoio O(log n)O(log n)} pesquisa, inserção e remoção. Árvores AVL podem ser coloridas vermelho-preto, assim são um subconjunto de árvores RB. Altura pior caso é 0.720 vezes a pior altura de árvores RB, então as árvores AVL são mais rigidamente equilibradas. As medições de desempenho de Ben Pfaff com casos de teste realistas em 79 corridas encontram rácios AVL a RB entre 0,677 e 1.077, mediana em 0.947 e média geométrica 0.910. As árvores da WAVL têm uma performance entre essas duas.
As árvores vermelhas-pretas também são particularmente valiosas na programação funcional, onde são uma das estruturas de dados persistentes mais comuns, usadas para conjuntos e conjuntos associativos que podem reter versões anteriores após mutações. A versão persistente de árvores vermelhas-pretas requer O(log n)O(log n)} espaço para cada inserção ou exclusão, além do tempo.
Para cada árvore 2–4, há árvores vermelho-pretas correspondentes com elementos de dados na mesma ordem. As operações de inserção e exclusão em 2–4 árvores também são equivalentes à inversão de cores e rotações em árvores vermelho-pretas. Isso faz de 2 a 4 árvores uma ferramenta importante para a compreensão da lógica por trás das árvores rubro-negras, e é por isso que muitos textos introdutórios sobre algoritmos introduzem 2 a 4 árvores logo antes das árvores rubro-negras, embora 2 a 4 árvores não sejam frequentemente usadas em prática.
Em 2008, Sedgewick introduziu uma versão mais simples da árvore rubro-negra chamada árvore rubro-negra inclinada para a esquerda, eliminando um grau de liberdade anteriormente não especificado na implementação. O LLRB mantém uma invariante adicional de que todos os links vermelhos devem inclinar-se para a esquerda, exceto durante inserções e exclusões. As árvores rubro-negras podem ser isométricas a 2–3 árvores ou 2–4 árvores, para qualquer sequência de operações. A isometria de 2–4 árvores foi descrita em 1978 por Sedgewick. Com 2–4 árvores, a isometria é resolvida por uma "mudança de cor" correspondendo a uma divisão, na qual a cor vermelha de dois nós filhos deixa os filhos e se move para o nó pai.
A descrição original da árvore do tango, um tipo de árvore otimizada para pesquisas rápidas, usa especificamente árvores rubro-negras como parte de sua estrutura de dados.
A partir de Java 8, o HashMap foi modificado tal que em vez de usar um LinkedList para armazenar diferentes elementos com hashcodes colidindo, uma árvore vermelha-preta é usada. Isso resulta na melhoria da complexidade do tempo de pesquisar tal elemento de O(m)O(m)} para O(log m){displaystyle O(log m)} Onde? mNão. é o número de elementos com hashcodes colidindo.
Operações
As operações somente leitura, como pesquisa ou traversal de árvore, em uma árvore vermelha-preta, não exigem nenhuma modificação daqueles usados para árvores de busca binárias, porque cada árvore vermelha-preta é um caso especial de uma simples árvore de pesquisa binária. No entanto, o resultado imediato de uma inserção ou remoção pode violar as propriedades de uma árvore vermelha-preta, cuja restauração é chamada reequilíbrio para que as árvores vermelhas-pretas se tornem auto-equilíbrio. Requer no pior caso um pequeno número, O(log n)O(log n)} na notação Big O, onde nNão. é o número de objetos na árvore, em média ou amortizado O(1)Não., um número constante, de alterações de cor (que são muito rápidas na prática); e não mais de três rotações de árvores (dois para inserção).
Se o exemplo de implementação abaixo não for adequado, outras implementações com explicações podem ser encontradas na biblioteca C anotada de Ben Pfaff, GNU libavl (v2.0.3 em junho de 2019).
Os detalhes das operações de inserção e remoção serão demonstrados com exemplo de código C++, que usa as definições de tipo, macros abaixo e a função auxiliar para rotações:
// Definições básicas do tipo:enum - Não. ( BLACK, RED }Estranho RBnode ( // nó de árvore vermelha-preta RBnode* pai; - Sim. NIL se raiz da árvore RBnode* criançaNão.2] - Sim. NIL se a criança estiver vazia // O índice é: // LEFT:= 0, if (key key) // DIREITO:= 1, se (key > parent->key) enum - Não. cor da cor; - Não. chave chave;}#define NIL NULL // ponteiro nulo ou ponteiro para nó senil#define LEFT 0#define RIGHT 1#define left child[LEFT]#define right child[RIGHT]Estranho RBtree ( // árvore vermelha-preta RBnode* raiz raiz; - Sim. NIL se a árvore estiver vazia}// Obter a direção da criança (∈ { esquerda, direita })// do non-root non-NIL RBnode* N:#define childDir(N) (N == (N->parent)->right ? DIREITO: À esquerda
rotação direita, animado.
RBnode* Rotação( RBtree* T, // árvore vermelha-preta RBnode* P, // raiz raiz de Suba (pode ser o raiz raiz de T) - Não. Dir.) ( // dir ∈ { esquerda, direita } RBnode* G = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = P- Sim.pai; RBnode* S = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = P- Sim.criançaNão.1- Não.Dir.] RBnode* C; Afirmar(S ! NIL); // ponteiro para o nó verdadeiro necessário C = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = S- Sim.criançaNão.Dir.] P- Sim.criançaNão.1- Não.Dir.] = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = C; se (C ! NIL) C- Sim.pai = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = P; S- Sim.criançaNão. Dir.] = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = P; P- Sim.pai = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = S; S- Sim.pai = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = G; se (G ! NULL) G- Sim.criançaNão. P - Sim. G- Sim.Certo. ? DIREITO : LEO ] = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = S; mais T- Sim.raiz raiz = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = S; retorno S; // nova raiz da subárvore?#define RotateDir(N,dir) RotateDirRoot(T,N,dir)#define RotateLeft(N) RotateDirRoot(T,N,LEFT)#define RotateRight(N) RotateDirRoot(T,N,RIGHT)
Notas ao código de exemplo e diagramas de inserção e remoção
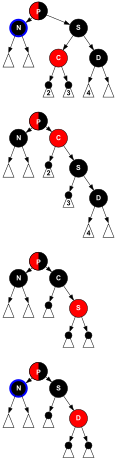
A proposta divide tanto a inserção quanto a remoção (sem falar em alguns casos muito simples), em seis constelações de nós, arestas e cores, que são chamadas de casos. A proposta contém para inserção e remoção, exatamente um caso que avança um nível de preto mais próximo da raiz e faz um loop, os outros cinco casos reequilibram a árvore por conta própria. Os casos mais complicados são representados em um diagrama.
 simboliza um nó vermelho e
simboliza um nó vermelho e  um (não-NIL) nó preto (de altura preta ≥ 1),
um (não-NIL) nó preto (de altura preta ≥ 1),  simboliza a cor vermelha ou preta de um nó não-NIL, mas a mesma cor ao longo do mesmo diagrama. NIL nós não são representados nos diagramas.
simboliza a cor vermelha ou preta de um nó não-NIL, mas a mesma cor ao longo do mesmo diagrama. NIL nós não são representados nos diagramas.- A variável N denota o nó atual, que é rotulado N ou N nos diagramas.
- Um diagrama contém três colunas e duas a quatro ações. A coluna esquerda mostra a primeira iteração, a coluna direita as iterações superiores, a coluna média mostra a segmentação de um caso em suas diferentes ações.
- A ação "entry" mostra a constelação de nós com suas cores que define um caso e principalmente viola alguns dos requisitos.
Uma borda azul toca o nó atual N e os outros nós são rotulados de acordo com sua relação com N. - Se uma rotação é considerada útil, isso é retratado na próxima ação, que é rotulada "rotação".
- Se alguma recoloração é considerada útil, isso é retratado na próxima ação, que é rotulada "cor".
- Se ainda houver alguma necessidade de reparo, os casos fazem uso de código de outros casos e isso após uma reassinação do nó atual N, que então novamente carrega um anel azul e relativo ao qual outros nós podem ter que ser reassinados também. Esta ação é rotulada "reassign".
Para ambos, insira e exclua, há (exatamente) um caso que itera um nível preto mais perto da raiz; então a constelação reassinada satisfaz o respectivo loop invariante.
- Um triângulo possivelmente numerado com um círculo preto no topo
 representa um subárvore vermelho-preto (conectado ao seu pai de acordo com a exigência 3) com uma altura preta igual ao nível de iteração menos um, ou seja, zero na primeira iteração. Sua raiz pode ser vermelha ou preta.
representa um subárvore vermelho-preto (conectado ao seu pai de acordo com a exigência 3) com uma altura preta igual ao nível de iteração menos um, ou seja, zero na primeira iteração. Sua raiz pode ser vermelha ou preta.
Um triângulo possivelmente numerado representa um subárvore vermelho-preto com uma altura preta um menos, ou seja, seu pai tem altura preta zero na segunda iteração.
representa um subárvore vermelho-preto com uma altura preta um menos, ou seja, seu pai tem altura preta zero na segunda iteração.
- Observação
- Para a simplicidade, o código de amostra usa a disjunção:
U == NIL || U->color == BLACK // considered black
- e a conjunção:
U != NIL && U->color == RED // not considered black
- Por isso, deve ser mantido em mente que ambas as declarações são não avaliado no total, se
U == NIL. Em ambos os casosU->colornão é tocado (veja Avaliação de curto-circuito).
(O comentárioconsidered blackestá de acordo com a exigência 2.) - O relacionado
if- as declarações têm de ocorrer muito menos frequentemente se a proposta for realizada.
Inserção
A inserção começa colocando o novo nó (não NIL), digamos N, na posição na árvore de pesquisa binária de um nó NIL cuja chave do predecessor em ordem compara menos que a do novo nó chave, que por sua vez compara menos que a chave de seu sucessor em ordem.
(Frequentemente, este posicionamento é o resultado de uma pesquisa dentro da árvore imediatamente anterior à operação de inserção e consiste em um nó P junto com uma direção dir com P->child[dir] == NIL.)
O nó recém-inserido é temporariamente colorido em vermelho para que todos os caminhos contenham o mesmo número de nós pretos que antes.
Mas se seu pai, digamos P, também for vermelho, então esta ação introduz uma violação de vermelho.
vazio RBinsert1( RBtree* T, // -> árvore vermelha-preta Estranho RBnode* N, // -> nó a ser inserido Estranho RBnode* P, // -> nó pai de N (pode ser NULL) bytes Dir.) // lado (LEFT ou RIGHT) de P onde inserir N( Estranho RBnode* G; // -> nó pai de P Estranho RBnode* U; // -> tio de N N- Sim.cor da cor = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = RED; N- Sim.esquerda = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = NIL; N- Sim.Certo. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = NIL; N- Sim.pai = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = P; se (P - Sim. NULL) ( // Não há pai T- Sim.raiz raiz = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = N; // N é a nova raiz da árvore T. retorno; // inserção completa ? P- Sim.criançaNão.Dir.] = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = N; // inserir N como dir-child de P // início do (do while)-loop: do (The rebalancing loop of the insert operation has the following invariant:
- A variável N, representando o nó atual N e inicialmente o nó de inserção, é feito a variável executando através do loop.
- N o
 (vermelho) no início de cada iteração.
(vermelho) no início de cada iteração. - Requisito 3 está satisfeito para todos os pares node¶parent com a possível exceção N←P quando P é também vermelho (violação vermelha em N).
- Todas as outras propriedades (incluindo a exigência 4) estão satisfeitas em toda a árvore.
Notas aos diagramas de inserção
- Nos diagramas, P é usado para N’ pai, G para o seu avó, e U pelo seu tio. Na tabela a — sinal indica raiz.
- Os diagramas mostram o nó pai P como a criança esquerda de seu pai G embora seja possível P estar de ambos os lados. O código de amostra cobre ambas as possibilidades por meio da variável lateral
dir. - Os diagramas mostram os casos em que P é vermelho também, o vermelho-violação.
- A coluna x indica a mudança na direção da criança, ou seja, o (para "outro") significa que P e N são ambas as crianças esquerda ou direita, enquanto i (para "inner") significa que a direção da criança muda de Ppara N’s.
- O grupo de colunas antes define o caso, cujo nome é dado na coluna Processo. Assim, os valores possíveis nas células deixadas vazias são ignorados. Assim, no caso de I2 o código de amostra cobre ambas as possibilidades de direções de crianças de N, embora o diagrama correspondente mostre apenas um.
- As linhas na sinopse são ordenadas de modo que a cobertura de todos os casos de RB possíveis é facilmente compreensível.
- A coluna rotação indica se uma rotação contribui para o reequilíbrio.
- A coluna atribuição mostra uma atribuição de N antes de entrar em um passo subsequente. Isso possivelmente induz uma reassinação dos outros nós P, G, U também.
- Se algo foi alterado pelo caso, isso é mostrado no grupo coluna depois.
- Um ✓ sinal na coluna Próximo significa que o reequilíbrio está completo com este passo. Se a coluna depois determina exatamente um caso, este caso é dado como o subsequente, caso contrário há pontos de interrogação.
- O loop está contido nas seções "Inserir caso I1" e "Inserir caso I2", onde no caso I2 o problema de reequilíbrio é escalado ? ? h= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2{displaystyle Delta h=2} níveis de árvore ou 1 nível preto superior na árvore, em que o avô G torna-se o novo nó atual N. Então, é preciso maximamente h2Não. passos de iteração para reparar a árvore (onde hNão. é a altura da árvore). Porque a probabilidade de escalada diminui exponencialmente com cada etapa o custo total de reequilíbrio é constante em média, de fato constante amortizada.
- Do corpo do loop, caso I1 sai por si mesmo e há sair ramos para os casos I4, I6, I5 + I6, e I3.
- Rotações ocorrem em casos I6 e I5 + I6 - fora do laço. Portanto, no máximo duas rotações ocorrem no total.
Inserir caso I1
O pai do nó atual P é preto, portanto o requisito 3 é válido. O requisito 4 também é válido de acordo com o invariante do loop.
se (P- Sim.cor da cor - Sim. BLACK) ( // Case_I1 (P black): retorno; // inserção completa ? // De agora em diante P é vermelho. se (G = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = P- Sim.pai) - Sim. NULL) Goto Processos; // P vermelho e raiz // outros: P red and G!=NULL. Dir. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = criança Dir.(P); // o lado do pai G no qual o nó P está localizado U = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = G- Sim.criançaNão.1- Não.Dir.] // tio se (U - Sim. NIL | U- Sim.cor da cor - Sim. BLACK) // considerado preto Goto Processo; // P red && U blackInserir caso I2
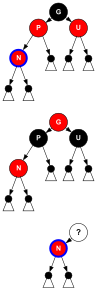
Se tanto o pai P quanto o tio U forem vermelhos, ambos poderão ser repintados de preto e o avô G ficará vermelho para manter o requisito 4. Como qualquer caminho através do pai ou do tio deve passar pelo avô, o número de nós pretos nesses caminhos não mudou. No entanto, o avô G pode agora violar o requisito 3, se tiver um progenitor vermelho. Depois de renomear G para N a invariante do loop é cumprida para que o rebalanceamento possa ser iterado em um nível de preto (= 2 níveis de árvore) acima.
// Case_I2 (P+U vermelho): P- Sim.cor da cor = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = BLACK; U- Sim.cor da cor = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = BLACK; G- Sim.cor da cor = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = RED; N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = G; // novo nó atual // iterate 1 nível preto superior // (= 2 níveis de árvore) ? enquanto (P = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = N- Sim.pai) ! NULL); // fim do (fazer enquanto)-loopInserir caso I3
Inserir caso I2 foi executado para h- Sim. - Sim. 12Não. Não. vezes e a altura total da árvore aumentou 1, agora sendo h.Não. H~.O nó atual N é a raiz (vermelho) da árvore, e todas as probabilidades de RB estão satisfeitas.
// Deixando o (fazer enquanto)-loop (depois de ter caído do Case_I2). // Case_I3: N é a raiz e o vermelho. retorno; // inserção completaInserir caso I4
O pai P é vermelho e a raiz. Como N também é vermelho, o requisito 3 foi violado. Mas depois de mudar a cor de P, a árvore fica em formato RB. A altura preta da árvore aumenta em 1.
Processos: // P é a raiz e o vermelho: P- Sim.cor da cor = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = BLACK; retorno; // inserção completaInserir caso I5
O pai P é vermelho, mas o tio U é preto. O objetivo final é girar o nó pai P para a posição do avô, mas isso não funcionará se N for um nó "interno" neto de G (ou seja, se N for o filho esquerdo do filho direito de G ou o filho direito do filho esquerdo filho de G). Uma rotação dir em P alterna as funções do nó atual N e seu pai P. A rotação adiciona caminhos através de N (aqueles na subárvore denominada 2, veja o diagrama) e remove caminhos através de P (aqueles na subárvore denominada 4). Mas tanto P quanto N são vermelhos, então o requisito 4 é preservado. O requisito 3 é restaurado no caso 6.
Processo: // P red && U black: se (N - Sim. P- Sim.criançaNão.1- Não.Dir.] ( // Case_I5 (P red && U black && N interior grandchild of G): Rotação(P,Dir.); // P nunca é a raiz N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = P; // novo nó atual P = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = G- Sim.criançaNão.Dir.] // novo pai de N // cair para Case_I6 ?Inserir caso I6
O nó atual N agora é certamente um nó "externo" neto de G (esquerda do filho esquerdo ou direita do filho direito). Agora (1-dir)-rotate em G, colocando P no lugar de G e tornando P o pai de N e G. G é preto e seu antigo filho P é vermelho, pois o requisito 3 foi violado. Depois de trocar as cores de P e G a árvore resultante satisfaz o requisito 3. O requisito 4 também permanece satisfeito, pois todos os caminhos que passaram pelo G agora passe pelo P preto.
// Case_I6 (P red && U black && N outer grandchild of G): Rotação(T,G,1- Não.Dir.); // G pode ser a raiz P- Sim.cor da cor = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = BLACK; G- Sim.cor da cor = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = RED; retorno; // inserção completa? // fim de RBinsert1Como o algoritmo transforma a entrada sem usar uma estrutura de dados auxiliar e usando apenas uma pequena quantidade de espaço de armazenamento extra para variáveis auxiliares, ele está no local.
Remoção
Casos simples
Did you mean:The label AND denotes the current node that at entry is the node to be deleted.
Se N for a raiz que não possui um filho não-NIL, ele será substituído por um nó NIL, após o qual a árvore estará vazia – e em formato RB.
Did you mean:If AND has exactly one non-NIL child, it must be a red child, according to conclusion 5.
Se N for um nó vermelho, ele não pode ter exatamente um filho não-NIL, porque este teria que ser preto pelo requisito 3. Além disso, não pode ter exatamente um filho preto de acordo com a conclusão 5. Como consequência, o nó vermelho N não tem nenhum filho e pode simplesmente ser removido.
Se N for um nó preto, ele pode ter dois filhos vermelhos, um único filho vermelho ou nenhum filho não-NIL. Se N tiver um único filho vermelho, ele será simplesmente substituído por este filho depois de pintar o último de preto.
Se N tem duas crianças não-NIL, uma navegação adicional para o elemento mínimo em seu subárvore direito (que é N’ s sucessor em ordem, diga Sim.- Sim.) encontra um nó com nenhum outro nó entre N e Sim.- Sim. (como mostrado aqui). Este nó Sim.- Sim. não tem uma criança esquerda e assim tem no máximo uma criança não-NIL. Se Sim.- Sim. é para ser removido Nlugar, os dados da árvore vermelha-preta relacionados com N e Sim.- Sim., ou seja, a cor de e os ponteiros para e dos dois nós, têm de ser trocados. (Como resultado, a árvore vermelha-preta modificada é a mesma que antes, exceto que a ordem entre N e Sim.- Sim. é revertida.) Esta escolha pode resultar em um dos casos mais simples acima, mas se Sim.- Sim. é sem criança e preto chegamos a...
Remoção de uma folha preta sem raiz
O caso complexo é quando N não é a raiz, é de cor preta e não tem filho próprio (⇔ apenas filhos NIL). Na primeira iteração, N é substituído por NIL.
vazio RBdelete2( RBtree* T, // -> árvore vermelha-preta Estranho RBnode* N) // -> nó a ser excluído ( Estranho RBnode* P = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = N- Sim.pai; // -> nó pai de N bytes Dir.; // lado de P no qual N está localizado (∈ { LEFT, RIGHT }) Estranho RBnode* S; // -> irmão de N Estranho RBnode* C; // -> sobrinho próximo Estranho RBnode* D; // -> sobrinho distante // P! NULL, já que N não é a raiz. Dir. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = criança Dir.(N); // lado do pai P no qual o nó N está localizado // Substituir N em seu pai P por NIL: P- Sim.criançaNão.Dir.] = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = NIL; Goto Start_D; // saltar para o loop // início do (do while)-loop: do ( Dir. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = criança Dir.(N); // lado do pai P no qual o nó N está localizadoStart_D: S = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = P- Sim.criançaNão.1- Não.Dir.] // irmão de N (tem altura preta >= 1) D = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = S- Sim.criançaNão.1- Não.Dir.] // sobrinho distante C = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = S- Sim.criançaNão. Dir.] // fechar sobrinho se (S- Sim.cor da cor - Sim. RED) Goto Processos; // S red===> P+C+D preto // S é preto: se (D ! NIL > D- Sim.cor da cor - Sim. RED) // não considerado preto Goto Processo; // D red && S black se (C ! NIL > C- Sim.cor da cor - Sim. RED) // não considerado preto Goto Processos; // C red && S+D black // Aqui ambos os sobrinhos são == NIL (primeira iteração) ou preto (mais tarde). se (P- Sim.cor da cor - Sim. RED) Goto Processos; // P red && C+S+D blackO loop de rebalanceamento da operação de exclusão tem a seguinte invariante:
- No início de cada iteração a altura preta de N igual ao número de iteração menos um, o que significa que na primeira iteração é zero e que N é um verdadeiro nó negro
 em iterações mais altas.
em iterações mais altas. - O número de nós negros nos caminhos através N é um menos do que antes da exclusão, ao passo que é inalterado em todos os outros caminhos, de modo que haja uma violência negra em P se existirem outros caminhos.
- Todas as outras propriedades (incluindo a exigência 3) estão satisfeitas em toda a árvore.
Notas para os diagramas de exclusão
- Nos diagramas abaixo, P é usado para N’ pai, S para o irmão de N, C (significante) perto para S’ criança na mesma direção que Ne D (significante) distante distante distante distante para Soutra criança (S não pode ser um nó NIL na primeira iteração, porque deve ter altura preta um, que foi a altura preta N antes de sua exclusão, mas C e D pode ser NIL nós).
- Os diagramas mostram o nó atual N como a criança esquerda de seu pai P embora seja possível N estar de ambos os lados. As amostras de código cobrem ambas as possibilidades por meio da variável lateral
dir. - No início (na primeira iteração) da remoção, N é o nó NIL substituindo o nó a ser excluído. Porque a sua localização no nó dos pais é a única coisa de importância, é simbolizada por
 (significante: o nó atual N é um nó NIL e uma criança esquerda) na coluna esquerda dos diagramas de exclusão. À medida que a operação prossegue também os nós adequados (de altura preta ≥ 1) podem tornar-se atuais (ver e. g. caso D2).
(significante: o nó atual N é um nó NIL e uma criança esquerda) na coluna esquerda dos diagramas de exclusão. À medida que a operação prossegue também os nós adequados (de altura preta ≥ 1) podem tornar-se atuais (ver e. g. caso D2). - Contando as balas pretas (
 e
e  ) em um diagrama de exclusão pode ser observado que os caminhos através N tem uma bala menos do que os outros caminhos. Isto significa uma violência negra P— se existir.
) em um diagrama de exclusão pode ser observado que os caminhos através N tem uma bala menos do que os outros caminhos. Isto significa uma violência negra P— se existir. - A constelação de cores no grupo de colunas antes define o caso, cujo nome é dado na coluna Processo. Assim, os valores possíveis nas células deixadas vazias são ignorados.
- As linhas na sinopse são ordenadas de modo que a cobertura de todos os casos de RB possíveis é facilmente compreensível.
- A coluna rotação indica se uma rotação contribui para o reequilíbrio.
- A coluna atribuição mostra uma atribuição de N antes de entrar em uma etapa de iteração subsequente. Isso possivelmente induz uma reassinação dos outros nós P, C, S, D também.
- Se algo foi alterado pelo caso, isso é mostrado no grupo coluna depois.
- Um ✓ sinal na coluna Próximo significa que o reequilíbrio está completo com este passo. Se a coluna depois determina exatamente um caso, este caso é dado como o subsequente, caso contrário há pontos de interrogação.
- O loop está contido nas seções de
Start_Datravés de "Delete case D2", onde o problema do reequilíbrio é escalado ? ? h= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1{displaystyle Delta h=1} nível superior na árvore em que o pai P torna-se o novo nó atual N. Então, é preciso maximamente hNão. iterações para reparar a árvore (onde hNão. é a altura da árvore). Porque a probabilidade de escalada diminui exponencialmente com cada iteração o custo total de reequilíbrio é constante em média, de fato constante amortizada. (Assim como um lado: Mehlhorn & Sanders apontam: "AVL árvores fazem não suportar custos constantes de atualização amortizada." Isso é verdade para o reequilíbrio após uma exclusão, mas não inserção AVL.) - Fora do corpo do laço há saída de ramos para os casos D3, D6, D5 + D6, D4, e D1; seção "Caso excluído D3" de seu próprio tem três diferentes ramos de saída para os casos D6, D5 e D4.
- Rotações ocorrem em casos D6 e D5 + D6 e D3 + D5 + D6 - todos fora do loop. Portanto, no máximo três rotações ocorrem no total.
Excluir caso D1
O nó atual N é a nova raiz. Um nó preto foi removido de cada caminho, portanto as propriedades do RB são preservadas. A altura preta da árvore diminui em 1.
// Case_D1 (P == NULL): retorno; // eliminação completaExcluir caso D2
Os filhos deP, S e S são negros. Depois de pintar S de vermelho, todos os caminhos que passam por S, que são precisamente aqueles caminhos que não passam por N, têm um menos nó preto. Agora todos os caminhos na subárvore enraizados em P têm o mesmo número de nós pretos, mas um a menos que os caminhos que não passam por P, então o requisito 4 ainda pode ser violado. Depois de renomear P para N, a invariante do loop é cumprida para que o rebalanceamento possa ser iterado em um nível de preto (= 1 nível de árvore) acima.
// Case_D2 (P+C+S+D black): S- Sim.cor da cor = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = RED; N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = P; // novo nó atual (talvez a raiz) // iterar 1 nível preto // (= 1 nível de árvore) superior ? enquanto (P = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = N- Sim.pai) ! NULL); // fim do (fazer enquanto)-loopExcluir caso D3
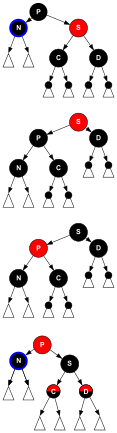
O irmão S é vermelho, então P e os sobrinhos C e D têm que ser pretos. Uma rotação dir em P transforma S em N é avô.
Então, depois de inverter as cores de P e S, o caminho através de N ainda tem um nó preto curto. Mas N agora tem um pai vermelho P e após a reatribuição um irmão preto S, então as transformações nos casos D4, D5 ou D6 são capaz de restaurar a forma RB.
Processos: // S red && P+C+D black: Rotação(T,P,Dir.); // P pode ser a raiz P- Sim.cor da cor = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = RED; S- Sim.cor da cor = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = BLACK; S = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = C; - Sim. NIL // now: P red && S black D = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = S- Sim.criançaNão.1- Não.Dir.] // sobrinho distante se (D ! NIL > D- Sim.cor da cor - Sim. RED) Goto Processo; // D red && S black C = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = S- Sim.criançaNão. Dir.] // fechar sobrinho se (C ! NIL > C- Sim.cor da cor - Sim. RED) Goto Processos; // C red && S+D black // Caso contrário, C+D considerou preto. // cair para Case_D4Excluir caso D4
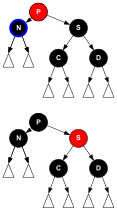
O irmão S e os filhos de S são negros, mas P é vermelho. Trocar as cores de S e P não afeta o número de nós pretos nos caminhos que passam por S, mas adiciona um ao número de nós pretos em caminhos que passam por N, compensando o nó preto excluído nesses caminhos.
Processos: // P red && S+C+D black: S- Sim.cor da cor = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = RED; P- Sim.cor da cor = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = BLACK; retorno; // eliminação completaExcluir caso D5
O irmão S é preto, Scriança próxima C é vermelho, e Scriança distante D é preto. Depois de um (1-dir)-Rotação em S o sobrinho C torna-se S’ pai e N’ s novo irmão. As cores de S e C são trocados.
Todos os caminhos ainda têm o mesmo número de nós negros, mas agora N tem um irmão negro cuja criança distante é vermelha, então a constelação é adequada para o caso D6. Nem sequer. N nem seus pais P são afetados por esta transformação, e P pode ser vermelho ou preto (![]() no diagrama).
no diagrama).
Processos: // C red && S+D black: Rotação(S,1- Não.Dir.); // S nunca é a raiz S- Sim.cor da cor = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = RED; C- Sim.cor da cor = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = BLACK; D = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = S; S = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = C; // now: D red && S black // cair para Case_D6Excluir caso D6
O irmão S é preto, Scriança distante D é vermelho. Depois de um dir-Rotação em P o irmão S torna-se o pai de P e Scriança distante D. As cores de P e S são trocados, e D é feito preto. Todo o subárvore ainda tem a mesma cor em sua raiz S, ou seja, vermelho ou preto (![]() no diagrama), que se refere à mesma cor antes e depois da transformação. Desta forma, a exigência 3 é preservada. Os caminhos no subárvore não passar N (i.o.w. passando por D e nó 3 no diagrama) passar pelo mesmo número de nós pretos como antes, mas N agora tem um ancestral preto adicional: ou P tornou-se preto, ou era preto e S foi adicionado como um avó preto. Assim, os caminhos que passam N passar por um nó preto adicional, de modo que a exigência 4 é restaurada e a árvore total está em forma de RB.
no diagrama), que se refere à mesma cor antes e depois da transformação. Desta forma, a exigência 3 é preservada. Os caminhos no subárvore não passar N (i.o.w. passando por D e nó 3 no diagrama) passar pelo mesmo número de nós pretos como antes, mas N agora tem um ancestral preto adicional: ou P tornou-se preto, ou era preto e S foi adicionado como um avó preto. Assim, os caminhos que passam N passar por um nó preto adicional, de modo que a exigência 4 é restaurada e a árvore total está em forma de RB.
Processo: // D red && S black: Rotação(T,P,Dir.); // P pode ser a raiz S- Sim.cor da cor = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = P- Sim.cor da cor; P- Sim.cor da cor = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = BLACK; D- Sim.cor da cor = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = BLACK; retorno; // eliminação completa? // fim de RBdelete2Como o algoritmo transforma a entrada sem usar uma estrutura de dados auxiliar e usando apenas uma pequena quantidade de espaço de armazenamento extra para variáveis auxiliares, ele está no local.
Prova de limites

cada um com número mínimo 1,2,4,6 resp. 10 de nós.
Para h∈ ∈ N{displaystyle hin mathbb Não. há uma árvore vermelha-preta de altura hNão. com
mhNão. m_{h}} = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2? ? (h+1)/2Gerenciamento de contas Gerenciamento de contas +2? ? h/2Gerenciamento de contas Gerenciamento de contas - Sim. - Sim. 2(h+1)/2rfloor }+2^{lfloor h/2rfloor - Sim. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(Não. = 2)) 2h2- Sim. - Sim. 2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2h2+1- Sim. - Sim. 2{displaystyle 2cdot 2^{tfrac {h}{2}}-2=2^{{tfrac Não. se hNão. mesmo 3)) 2h- Sim. - Sim. 12- Sim. - Sim. 2{displaystyle 3cdot 2^{tfrac Não. se hNão. O quê?
nós (? ? Gerenciamento de contas Gerenciamento de contas {displaystyle lfloor ,rfloor } é a função do chão) e não há árvore vermelha-preta desta altura da árvore com menos nós - por isso é mínimo.
Sua altura preta é ⌈ ⌈ h/2⌉ ⌉ {displaystyle lceil h/2rceil } (com raiz preta) ou para odd hNão. (então com uma raiz vermelha) também (h- Sim. - Sim. 1)/2.(h-1)/2~.}
- Prova
Para que uma árvore vermelho-preta de uma certa altura tenha um número mínimo de nós, ela deve ter exatamente um caminho mais longo com número máximo de nós vermelhos, para atingir uma altura máxima de árvore com uma altura preta mínima. Além deste caminho, todos os outros nós devem ser pretos. Se um nó for retirado desta árvore ele perde altura ou alguma propriedade RB.
A árvore RB de altura h= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1Não. com raiz vermelha é mínima. Isto está de acordo com
- m1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2? ? (1+1)/2Gerenciamento de contas Gerenciamento de contas +2? ? 1/2Gerenciamento de contas Gerenciamento de contas - Sim. - Sim. 2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =21+20- Sim. - Sim. 2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1.Não. m_{1}=2^{lfloor (1+1)/2rfloor }!+!2^{lfloor 1/2rfloor }!!-!! 2=2^{1}!+!2^{0}!!-!!2=1~.}
Uma árvore RB mínima (RBh na figura 4) da altura 1}" xmlns="http://www.w3.org/1998/Math/MathML">h>1Não.1}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/3df33213a54649226c03c8115b130c49170d0683" style="vertical-align: -0.338ex; width:5.6ex; height:2.176ex;"/> tem uma raiz cujas duas subárvores de criança são de altura diferente. O subárvore superior da criança também é uma árvore RB mínima, RBh-1, contendo também um caminho mais longo que define sua altura h- Sim. - Sim. 1Não. h!!-!; ele tem mh- Sim. - Sim. 1Não. m_{h-1}} nós e a altura preta ? ? (h- Sim. - Sim. 1)/2Gerenciamento de contas Gerenciamento de contas =S.{displaystyle lfloor (h!!-!!1)/2rfloor - Sim. O outro subárvore é uma árvore binária perfeita de (preto) altura SNão. tendo em conta que 2S- Sim. - Sim. 1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2? ? (h- Sim. - Sim. 1)/2Gerenciamento de contas Gerenciamento de contas - Sim. - Sim. 1{displaystyle 2^{s}!!-!!1=2^{lfloor (h-1)/2rfloor }!!-! nós pretos - e nenhum nó vermelho. Então o número de nós é por indução
| mhNão. m_{h}} | = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não. | (mh- Sim. - Sim. 1)(m_{h-1})} | +Sim. | (1)Não. | +Sim. | (2? ? (h- Sim. - Sim. 1)/2Gerenciamento de contas Gerenciamento de contas - Sim. - Sim. 1)(h-1)/2rfloor }-1)} | ||||
| (subárvore superior) | (raiz) | (segunda subárvore) | ||||||||
| resultando em | ||||||||||
| mhNão. m_{h}} | = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não. | (2? ? h/2Gerenciamento de contas Gerenciamento de contas +2? ? (h- Sim. - Sim. 1)/2Gerenciamento de contas Gerenciamento de contas - Sim. - Sim. 2){displaystyle (2^{lfloor h/2rfloor }+2^{lfloor (h-1)/2rfloor }-2)} | +Sim. | 2? ? (h- Sim. - Sim. 1)/2Gerenciamento de contas Gerenciamento de contas {displaystyle 2^{lfloor (h-1)/2rfloor }} | ||||||
| = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não. | 2? ? h/2Gerenciamento de contas Gerenciamento de contas +2? ? (h+1)/2Gerenciamento de contas Gerenciamento de contas - Sim. - Sim. 2{displaystyle 2^{lfloor h/2rfloor }+2^{lfloor (h+1)/2rfloor - Sim.■ | |||||||||
O gráfico da função mhNão. m_{h}} é convexo e linear com pontos de interrupção em (h= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2k|m2k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2)) 2k- Sim. - Sim. 2)(h=2k;|;m_{2k}=2cdot 2^{k}!-!2)} Onde? k∈ ∈ N.{displaystyle kin mathbb Não. A função foi tabulada como mh= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não. - Sim. A027383 (h– 1) para h≥ ≥ 1{displaystyle hgeq 1} (sequência) A027383 no OEIS).
- Resolvendo a função para hNão.
A desigualdade 8=2^{3}}" xmlns="http://www.w3.org/1998/Math/MathML">9>8= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =23Não. 9>8=2^{3}}8=2^{3}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9fc6aa3b743ffc4de7d75d22ec4e30b93ae86037" style="vertical-align: -0.338ex; width:10.739ex; height:2.676ex;"/> para a 2^{3/2}}" xmlns="http://www.w3.org/1998/Math/MathML">3>23/2Não. 3>2^{3/2}}
2^{3/2}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/289041b8c90d373cd5129f1c257ef854de064e4c" style="vertical-align: -0.338ex; width:8.122ex; height:2.843ex;"/>, que para odd hNão. para a
- 2cdot 2^{h/2}-2}" xmlns="http://www.w3.org/1998/Math/MathML">mh= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =3)) 2(h- Sim. - Sim. 1)/2- Sim. - Sim. 2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(3)) 2- Sim. - Sim. 3/2))) 2(h+2)/2- Sim. - Sim. 2>2)) 2h/2- Sim. - Sim. 2Não. m_{h}=3cdot 2^{(h-1)/2}-2={bigl (}3cdot 2^{-3/2}{bigr)}cdot 2^{(h+2)/2}-2>2cdot 2^{h/2}-2}
2cdot 2^{h/2}-2}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/11105813afbd3e754a837dae4eb53795fdf60696" style="vertical-align: -1.005ex; width:60.712ex; height:3.509ex;"/>.
Então, em ambos, o caso uniforme e estranho, hNão. está no intervalo
| log2 (n+1)(n+1)} | ≤ ≤ h≤ ≤ {displaystyle leq hleq } | 2log2 (n+2)- Sim. - Sim. 2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2log2 (n/2+1){displaystyle 2log _{2}(n+2)-2=2log _{2}(n/2+1)} | <math alttext="{displaystyle {bigl [}Não.<2log2 (n+1)][}<2log _{2}(n+1;{bigr ]<img alt="{displaystyle {bigl [} | |
| (arvore binário perfeito) | (vermelha mínima - árvore preta) |
com nNão. ser o número de nós.
- Conclusão
Uma árvore vermelha-preta com nNão. nós (chaves) tem altura da árvore h∈ ∈ O(log n).{displaystyle hin O(log n).}
Definir operações e operações em massa
Além das operações de inserção, exclusão e pesquisa de elemento único, diversas operações de conjunto foram definidas em árvores vermelho-preto: união, interseção e diferença de conjunto. Então, operações rápidas em massa em inserções ou exclusões podem ser implementadas com base nessas funções definidas. Essas operações de conjunto dependem de duas operações auxiliares, Split e Join. Com as novas operações, a implementação de árvores rubro-negras pode ser mais eficiente e altamente paralelizável. Para atingir suas complexidades de tempo, esta implementação requer que a raiz possa ser vermelha ou preta, e que cada nó armazene sua própria altura preta.
- Participe: A função Participe está em duas árvores vermelhas-pretas )1 e )2 e uma chave k, onde )1 < k < )2Todas as chaves )1 são menos do que ke todas as chaves )2 são maiores do que k. Ele retorna uma árvore contendo todos os elementos em )1, )2 também k.
- Se as duas árvores tiverem a mesma altura preta, Participe simplesmente cria um novo nó com subárvore esquerdo )1, raiz k e subárvore direito )2. Se ambos )1 e )2 tem raiz preta, conjunto k para ser vermelho. Caso contrário, k é preto.
- Se as alturas pretas são desiguais, suponha que )1 tem maior altura preta do que )2 (o outro caso é simétrico). Participe segue a espinha direita de )1 até um nó negro c, que é equilibrado com )2. Neste ponto um novo nó com a criança esquerda c, raiz k (definido para ser vermelho) e criança direita )2 é criado para substituir c. O novo nó pode invalidar o vermelho-preto invariante porque no máximo três nós vermelhos podem aparecer em uma linha. Isso pode ser corrigido com uma rotação dupla. Se o problema vermelho duplo se propaga para a raiz, a raiz é então definida para ser preta, restaurando as propriedades. O custo desta função é a diferença das alturas pretas entre as duas árvores de entrada.
- Divisão: Para dividir uma árvore vermelha-preta em duas árvores menores, as menores que a chave x, e os maiores que a chave x, primeiro desenhar um caminho da raiz, inserindo x na árvore vermelha-preta. Após esta inserção, todos os valores menos do que x será encontrado à esquerda do caminho, e todos os valores maiores do que x será encontrado à direita. Aplicando-se Participe, todas as subárvores do lado esquerdo são fundidas inferior-up usando chaves no caminho como nós intermediários de baixo para cima para formar a árvore esquerda, e a parte direita é simétrica.
- Para algumas aplicações, Divisão também retorna um valor booleano denotando se x aparece na árvore. O custo de Divisão o O(log n),{displaystyle O(log n),} ordem da altura da árvore. Este algoritmo não tem nada a ver com quaisquer propriedades especiais de uma árvore vermelha-preta, e pode ser usado em qualquer árvore com uma Junte-se operação, como uma árvore AVL.
O algoritmo de junção é o seguinte:
função junçãoRightRB (TL, k, TR:
se (T)L.color=preto) e (TL- BlackHeight - TR.blackHeight:
retorno Node (T)L,,,,,,R)
T'=Node (T)L.left,L.key, TL.color>,joinRightRB(TL.right,k,TR)
se (T)L.color=preto) e (T'.right.color=T'.right.right.color=vermelho):
T'.right.right.color=preto;
retorno rotateLeft(T')
retorno T'*[recte T] *
função se juntarLeftRB (TL, k, TR:
/* simétrico para se juntar RB */
função ingressar(TL, k, TR:
se TL.blackHeight> TR.blackHeight:
T'=joinRightRB(T)L,k,TR)
se (T'.color=vermelho) e (T'.right.color=vermelho):
T'.color
retorno T
se TR.blackHeight> TL.blackHeight:
/* simétricos */
se (T)L.color=preto) e (TR.color=preto):
retorno Node (T)L,,,,,,R)
retorno Node (T)L, , TR)
O algoritmo de divisão é o seguinte:
função split(T, k): se (T = nil) retorno (nil, false, nil) se (k = T.key) retorno (T.left, true, T.right) se (k < T.key): (L',b,R') = split (T.left, k) retorno (L',b,join (R',T.key,T.right)) (L',b,R') = split (T.right, k) retorno (join (T.left,T.key,L'),b,T.right)
A união de duas árvores rubro-negras t1 e t2 representando os conjuntos A e B, é uma árvore vermelho-preta t que representa A ∪ B. A seguinte função recursiva calcula esta união:
função união (t)1,2: se)1 = nil retorno)2 se)2 = nil retorno)1(L)1,b,R1)1,2.key) - Sim.início: TL= união (L1,2.left) - Não.início: TR= união (R)1,2.right) Espera. Proc. 2 retorno ingressar(TL,2.key, TR)
Aqui, presume-se que split retorne duas árvores: uma contendo as chaves menos sua chave de entrada, a outra contendo as chaves maiores. (O algoritmo não é destrutivo, mas também existe uma versão destrutiva no local.)
O algoritmo para interseção ou diferença é semelhante, mas requer a rotina auxiliar Join2 que é igual a Join, mas sem a chave do meio. Com base nas novas funções de união, intersecção ou diferença, uma chave ou múltiplas chaves podem ser inseridas ou excluídas da árvore rubro-negra. Como Split chama Join mas não lida diretamente com os critérios de balanceamento das árvores rubro-negras, tal implementação é geralmente chamada de implementação "baseada em junção" implementação.
A complexidade de cada união, interseção e diferença é O(mlog (nm+1))Não. Oleft(mlog left({n over m}+1right)right)} para duas árvores vermelhas-pretas de tamanhos mNão. e n(≥ ≥ m){displaystyle n(geq m)}. Esta complexidade é ideal em termos do número de comparações. Mais importante, uma vez que as chamadas recursivas para união, interseção ou diferença são independentes umas das outras, elas podem ser executadas em paralelo com uma profundidade paralela O(log mlog n)Não. O(log mlog n)}. Quando m= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1Não., a implementação baseada na união tem o mesmo gráfico cíclico direcionado computacional (DAG) como inserção e exclusão de elementos únicos se a raiz da árvore maior é usada para dividir a árvore menor.
Algoritmos paralelos
Algoritmos paralelos para a construção de árvores vermelhas-pretas de listas ordenadas de itens podem ser executados em tempo constante ou O(log log n)Não. O(log log n)} tempo, dependendo do modelo do computador, se o número de processadores disponíveis é assintoticamente proporcional ao número nNão. de itens onde n→ → ∞ ∞ {displaystyle nto infty }. Pesquisa rápida, inserção e eliminação algoritmos paralelos também são conhecidos.
Os algoritmos baseados em junção para árvores rubro-negras são paralelos para operações em massa, incluindo união, interseção, construção, filtro, redução de mapa e assim por diante.
Operações em massa paralelas
Operações básicas como inserção, remoção ou atualização podem ser paralelizadas definindo operações que processam volumes de vários elementos. Também é possível processar bulks com diversas operações básicas, por exemplo os bulks podem conter elementos para inserir e também elementos para remover da árvore.
Os algoritmos para operações a granel não são apenas aplicáveis à árvore vermelha-preta, mas podem ser adaptados a outras estruturas de dados de sequência ordenada também, como a árvore 2-3, árvore 2-3-4 e (a,b)-árvore. Nos seguintes algoritmos diferentes para inserção em massa serão explicados, mas os mesmos algoritmos também podem ser aplicados à remoção e atualização. A inserção em massa é uma operação que insere cada elemento de uma sequência Eu...Não. Eu... em uma árvore TNão. T..
Com base em junção
Esta abordagem pode ser aplicada a cada estrutura de dados de sequência ordenada que suporta operações de junção e divisão eficientes. A ideia geral é dividir Eu...Não. Eu... e TNão. T. em várias partes e executar as inserções nestas partes em paralelo.
- Primeiro o volume Eu...Não. Eu... de elementos para inserir deve ser classificado.
- Depois disso, o algoritmo se divide Eu...Não. Eu... para dentro k∈ ∈ N+{displaystyle kin mathbb (N} ^{+}} peças ⟨ ⟨ Eu...1,⋯ ⋯ ,Eu...k)) {displaystyle langle I_{1},cdotsI_{k}rangle } de aproximadamente tamanhos iguais.
- Próximo da árvore TNão. T. deve ser dividido em kNão. peças ⟨ ⟨ T1,⋯ ⋯ ,Tk)) {displaystyle langle T_{1},cdotsT_{k}rangle } de uma maneira, de modo que para cada <math alttext="{displaystyle jin mathbb {N} ^{+}|,1leq jJJ∈ ∈ N+|1≤ ≤ JJ<k{displaystyle jin mathbb {N} ^{+}|,1leq Não.<img alt="{displaystyle jin mathbb {N} ^{+}|,1leq j seguintes restrições de retenção:
- <math alttext="{displaystyle {text{last}}(I_{j})último(Eu...JJ)<Primeiro primeiro.(TJJ+1){displaystyle {text{last}}(I_{j})<{text{first}}(T_{j+1})}<img alt="{displaystyle {text{last}}(I_{j})
- <math alttext="{displaystyle {text{last}}(T_{j})último(TJJ)<Primeiro primeiro.(Eu...JJ+1){displaystyle {text{last}}(T_{j})<{text{first}}(I_{j+1})}<img alt="{displaystyle {text{last}}(T_{j})
- Agora o algoritmo insere cada elemento de Eu...JJNão. I_{j}} para dentro TJJNão. T_{j}} sequencialmente. Este passo deve ser realizado para cada JJNão., que pode ser feito até kNão. processadores em paralelo.
- Finalmente, as árvores resultantes serão unidas para formar o resultado final de toda a operação.
Note que no Passo 3 as restrições para dividir Eu...Não. Eu... assegurar que na etapa 5 as árvores podem ser unidas novamente e a sequência resultante é ordenada.
árvore inicial
dividir I e T
inserir na divisão T
Junte-se a T
O pseudocódigo mostra uma implementação simples de divisão e conquista do algoritmo baseado em junção para inserção em massa. Ambas as chamadas recursivas podem ser executadas em paralelo. A operação de junção usada aqui difere da versão explicada neste artigo; em vez disso, é usado join2, que perde o segundo parâmetro k.
Inserir volume(T, I, K): I.sort() bulklInsertRec (T, I, k) volumeInserirRec(T, I, K): se k = 1: para todos e em I: T.insert(e) maism:= ∴size(I) / 2 certificados (T)1T2:= split(T, I[m]) volumeInserirRec (T1, I[0.. m], kk / 2)) | bulkInsertRec(T2, I[m + 1.. size(I) - 1], ∴k / 2 Tagged) T ← join2(T)1, T2)
Tempo de execução
Classificação Eu...Não. Eu... não é considerado nesta análise.
| Níveis de recuperação | ∈ ∈ O(log k){displaystyle in O(log k)} |
| T(split) + T(join) | ∈ ∈ O(log |T|){displaystyle in O(log |T|)} |
| inserções por rosca | ∈ ∈ O(|Eu...|k){displaystyle in Oleft({frac {|I|}{k}}right)} |
| T (inserir) | ∈ ∈ O(log |T|){displaystyle in O(log |T|)} |
| T (bulkInsert) com kNão. = #processadores | ∈ ∈ O(log klog |T|+|Eu...|klog |T|){displaystyle in Oleft(log klog |T|+{frac {|I|}{k}}log |T|right)} |
Isso pode ser melhorado usando algoritmos paralelos para dividir e se juntar. Neste caso, o tempo de execução é ∈ ∈ O(log |T|+|Eu...|klog |T|){displaystyle in Oleft(log |T|+{frac {|I|}{k}}log |T|right)}.
Trabalho
| #splits, #joins | ∈ ∈ O(k){displaystyle in O(k)} |
| W(split) + W(join) | ∈ ∈ O(log |T|){displaystyle in O(log |T|)} |
| #inserções | ∈ ∈ O(|Eu...|){displaystyle in O(|I|)} |
| W(inserir) | ∈ ∈ O(log |T|){displaystyle in O(log |T|)} |
| W(bulkInsert) | ∈ ∈ O(klog |T|+|Eu...|log |T|){displaystyle in O(klog |T|+|I|log |T|)} |
Pipelining
Outro método de paralelizar operações em massa é usar uma abordagem de pipeline. Isto pode ser feito dividindo a tarefa de processar uma operação básica em uma sequência de subtarefas. Para múltiplas operações básicas, as subtarefas podem ser processadas em paralelo, atribuindo cada subtarefa a um processador separado.
- Primeiro o volume Eu...Não. Eu... de elementos para inserir deve ser classificado.
- Para cada elemento em Eu...Não. Eu... o algoritmo localiza a posição de inserção de acordo em TNão. T.. Isso pode ser feito em paralelo para cada elemento ∈ ∈ Eu...- Sim. desde então TNão. T. Não será mutado neste processo. Agora! Eu...Não. Eu... deve ser dividido em subsequências SNão. S. de acordo com a posição de inserção de cada elemento. Por exemplo Sn,Eu...ef){displaystyle s_{n,{mathit {left}}}}}} é a subsequência de Eu...Não. Eu... que contém os elementos cuja posição de inserção seria à esquerda do nó nNão..
- O elemento central mn,DEu...R{displaystyle m_{n,{mathit {dir}}}}}} de cada subsequência Sn,DEu...R{displaystyle s_{n,{mathit {dir}}}}}} será inserido TNão. T. como um novo nó n?Não.. Isso pode ser feito em paralelo para cada mn,DEu...R{displaystyle m_{n,{mathit {dir}}}}}} desde por definição a posição de inserção de cada mn,DEu...R{displaystyle m_{n,{mathit {dir}}}}}} é único. Se Sn,DEu...R{displaystyle s_{n,{mathit {dir}}}}}} contém elementos à esquerda ou à direita de mn,DEu...R{displaystyle m_{n,{mathit {dir}}}}}}, estes serão contidos em um novo conjunto de subsequências SNão. S. como Sn?,Eu...ef){displaystyle s_{n',{mathit {left}}}}}} ou Sn?,REu...gh){displaystyle s_{n',{mathit {right}}}}}}.
- Agora! TNão. T. possivelmente contém até dois nós vermelhos consecutivos no final dos caminhos formam a raiz para as folhas, que precisa ser reparado. Note que, ao reparar, a posição de inserção dos elementos ∈ ∈ S{displaystyle in S} tem que ser atualizado, se os nós correspondentes são afetados por rotações.
Se dois nós têm diferentes ancestrais negros mais próximos, eles podem ser reparados em paralelo. Uma vez que no máximo quatro nós podem ter o mesmo ancestral preto mais próximo, os nós no nível mais baixo podem ser reparados em um número constante de etapas paralelas.
Este passo será aplicado sucessivamente aos níveis negros acima até TNão. T. é totalmente reparado. - Os passos 3 a 5 serão repetidos nas novas subsequências até SNão. S. está vazio. Neste ponto cada elemento ∈ ∈ Eu...- Sim. foi inserido. Cada aplicação destas etapas é chamada de estágio. Desde o comprimento das subsequências em SNão. S. o ∈ ∈ O(|Eu...|){displaystyle in O(|I|)} e em cada etapa as subsequências estão sendo cortadas na metade, o número de etapas é ∈ ∈ O(log |Eu...|){displaystyle in O(log |I|)}.
Uma vez que todas as etapas movem os níveis negros da árvore, eles podem ser paralelos em um pipeline. Uma vez que um estágio terminou o processamento de um nível preto, a próxima etapa é capaz de se mover e continuar nesse nível.
Árvore inicial
Encontrar posições de inserção
Etapa 1 insere elementos
Estágio 1 começa a reparar nós
Etapa 2 insere elementos
Estágio 2 começa a reparar nós
Etapa 3 insere elementos
Estágio 3 começa a reparar nós
A fase 3 continua a reparar nós
Tempo de execução
Classificação Eu...Não. Eu... não é considerado nesta análise. Também, |Eu...||I|} é assumido ser menor do que |T||T|}, caso contrário seria mais eficiente construir a árvore resultante do zero.
| T (posição de inserção final) | ∈ ∈ O(log |T|){displaystyle in O(log |T|)} |
| #stages | ∈ ∈ O(log |Eu...|){displaystyle in O(log |I|)} |
| T(inserir) + T(reparar) | ∈ ∈ O(log |T|){displaystyle in O(log |T|)} |
| T (bulkInsert) com |Eu...||I|} #processadores # | ∈ ∈ O(log |Eu...|+2)) log |T|){displaystyle in O(log |I|+2cdot log |T|)} = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =O(log |T|){displaystyle =O(log |T|)} |
Trabalho
| W (posição de inserção final) | ∈ ∈ O(|Eu...|log |T|){displaystyle in O(|I|log |T|)} |
| #inserções, #repairs | ∈ ∈ O(|Eu...|){displaystyle in O(|I|)} |
| W(inserir) + W(reparar) | ∈ ∈ O(log |T|){displaystyle in O(log |T|)} |
| W(bulkInsert) | ∈ ∈ O(2)) |Eu...|log |T|){displaystyle in O(2cdot |I|log |T|)} = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =O(|Eu...|log |T|){displaystyle =O(|I|log |T|)} |
Cultura popular
Uma árvore rubro-negra foi referenciada corretamente em um episódio de Missing, conforme observado por Robert Sedgewick em uma de suas palestras:
- Jess.:
Era a porta vermelha outra vez.
Pollock:Pensei que a porta vermelha era o contentor de armazenamento.
Jess.:Mas já não era vermelho, era preto.
Antonio Antonio:O vermelho a virar para o preto significa o quê?
Pollock:Déficits orçamentais, tinta vermelha, tinta preta.
Antonio Antonio:Pode ser de uma árvore de busca binária. A árvore vermelha-preta rastreia cada caminho simples de um nó para uma folha descendente que tem o mesmo número de nós negros.
Jess.:Isso ajuda-te com as senhoras?
Referências e notas
- ↑ a b d Paton, James. "Red-Black Trees".
- ↑ a b reequilíbrio apenas (sem pesquisa), veja Tarjan e Mehlhorn.
- ↑ a b Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). «Red–Black Trees» (em inglês). Introdução aos Algoritmos (2a ed.). MIT Press. pp. 273–301. ISBN 978-0-262-03293-3.
- ^ Morris, John (1998). «Red–Black Trees» (em inglês). Estruturas de Dados e Algoritmos.
- ^ Bayer, Rudolf (1972). «Symmetric Binary B-Trees: Data structure and Maintenance Algoritmos» (em inglês). Acta Informatica. 1 (4): 290–306. doi:10.1007/BF00289509. S2CID 28836825.
- ^ Drozdek, Adam (2001). Estruturas de dados e algoritmos em Java (2 ed.). Sams Publishing. p. 323. ISBN 978-0534376680.
- ↑ a b Guibas, Leonidas J.; Sedgewick, Robert (1978). «A Dichromatic Framework for Balanced Trees» (em inglês). Proceedings of the 19th Annual Symposium on Foundations of Computer Sciencepp. 8–21. doi:10.1109/SFCS.1978.3.
- ^ «Red Black Trees» (em inglês). eternamenteconfuzzled.com. Arquivado do original em 2007-09-27. Retrieved 2015-09-02.
- ^ Sedgewick, Robert (2012). Red-Black BSTs. Coursera.
Muitas pessoas perguntam por que usamos o nome vermelho-preto. Bem, nós inventamos esta estrutura de dados, esta maneira de olhar para árvores equilibradas, no Xerox PARC que era a casa do computador pessoal e muitas outras inovações que vivemos com hoje entrando interfaces gráficas de usuário, Ethernet e programações orientadas a objetos[sic] e muitas outras coisas. Mas uma das coisas que foi inventada havia impressão a laser e estávamos muito animados para ter impressora a laser a cores nas proximidades que poderia imprimir as coisas na cor e fora das cores que o vermelho olhou o melhor. Então, é por isso que escolhemos a cor vermelha para distinguir links vermelhos, os tipos de links, em três nós. Então, isso é uma resposta para a pergunta para as pessoas que têm perguntado.
- ^ "De onde vem o termo "Red/Black Tree"?". Programadores.com. Retrieved 2015-09-02.
- ^ Andersson, Arne (1993-08-11). «Balanced search trees made simple» (em inglês). Em Dehne, Frank; Sack, Jörg-Rüdiger; Santoro, Nicola; Whitesides, Sue (eds.). Algoritmos e Estruturas de Dados (Processos). Notas de Palestra em Ciência da Computação. Vol. 709. Springer-Verlag Berlin Heidelberg. pp. 60–71. CiteSeerX10.1.1.118.6192. doi:10.1007/3-540-57155-8_236. ISBN 978-3-540-57155-1. Arquivado do original em 2018-12-08. URL do Alt
- ^ Okasaki, Chris (1999-01). «Red–black trees in a funcional setting» (em inglês). Jornal de Programação Funcional. 9 (4): 471–477.10.1017/S0956796899003494ISSN 1469-7653. S2CID 20298262.
- ^ Sedgewick, Robert (1983). Algoritmos (1a ed.). Addison-Wesley. ISBN 978-0-201-06672-2.
- ^ Sedgewick, Robert; Wayne, Kevin. "RedBlackBST.java". algs4.cs.princeton.edu. Retrieved 7 de Abril 2018.
- ^ Sedgewick, Robert (2008). «Left-leaning Red–Black Trees» (em inglês).
- ↑ a b c Sedgewick, Robert; Wayne, Kevin (2011). Algoritmos (4a ed.). Addison-Wesley Professional. ISBN 978-0-321-57351-3.
- ↑ a b d Mehlhorn, Kurt; Sanders, Peter (2008). "7. Sequências ordenadas" (PDF). Algoritmos e Estruturas de Dados: A caixa de ferramentas básica. Berlim/Heidelberg: Springer. CiteSeerX10.1.1.148.2305. doi:10.1007/978-3-540-77978-0. ISBN 978-3-540-77977-3.
- ↑ a b Cormen, Thomas; Leiserson, Charles; Rivest, Ronald; Stein, Clifford (2022). «13. Red-Black Trees» (em inglês). Introdução aos Algoritmos (4a ed.). MIT Press. pp. 331–332. ISBN 9780262046305.
- ^ Usando a definição de ordem de Knuth: o número máximo de crianças
- ^ Sedgewick, Robert (1998). Algoritmos em C++. Addison-Wesley Professional. pp. 565–575. ISBN 978-0-201-35088-3.
- ^ «The Implementation of epoll (1)» (em inglês). Setembro 2014.
- ^ Pfaff 2004
- ↑ a b "Robert Sedgewick" (PDF). Cs.princeton.edu. 4 de junho de 2020. Retrieved 26 de Março 2022.
- ^ Árvores Balanceadas (PDF). Cs.princeton.edu. Retrieved 26 de Março 2022.
- ^ Demaine, E. D.; Harmon, D.; Iacono, J.; Pătraşcu, M. (2007). "Otimidade dinâmica - quase" (PDF). SIAM Journal on Computing. 37 (1): 240. doi:10.1137/S0097539705447347. S2CID 1480961.
- ^ «How does a HashMap work in JAVA» (em inglês). coding-geek.com.
- ^ Tarjan, Robert Endre (abril de 1985). "Complexidade Computacional Amortizada" (PDF). SIAM Journal on Algebraic and Discrete Methods. 6 (2): 306–318. doi:10.1137/0606031.
- ^ O importante sobre essas rotações de árvores é que eles preservam a sequência em ordem dos nós da árvore.
- ^ «Ben Pfaff (2007): Versão HTML online de uma coleção bem documentada de árvore de pesquisa binária e rotinas de biblioteca de árvores balanceadas".
- ↑ a b As colunas esquerdas contêm muito menos nós do que as direitas, especialmente para remoção. Isso indica que alguma eficiência pode ser obtida puxando a primeira iteração dos loops de reequilíbrio de inserção e exclusão, porque muitos dos nós nomeados são nós NIL na primeira iteração e definitivamente não-NIL mais tarde. (Ver também esta observação.)
- ^ As rotações foram colocadas antes de recolorir por razões de clareza. Mas os dois comutam, de modo que é escolha livre para mover a rotação para a cauda.
- ↑ a b O mesmo particionamento é encontrado em Ben Pfaff.
- ^ Dinesh P. Mehta, Sartaj Sahni (Ed.) Manual de Estruturas de Dados e Aplicações 10.4.2
- ^ Igualdade no limite superior detém para as árvores RB mínimas RB2k de altura uniforme 2)) k- Sim. com n= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2)) 2k- Sim. - Sim. 2{displaystyle n=2cdot 2^{k}-2}} nós e só para aqueles. Assim, a desigualdade é marginalmente mais precisa do que a generalizada <math alttext="{displaystyle hh<2log2 (n+1),(n+1),}<img alt="{displaystyle h e. g. em Cormen p. 264.
Além disso, essas árvores são árvores binárias que admitem uma única coloração conforme os requisitos de RB 1 a 4. Mas há mais tais árvores, e. g. anexando um nó de criança a uma folha preta sempre força a vermelho. (Uma árvore RB mínima de altura ímpar permite virar a cor da raiz de vermelho para preto.) - ↑ a b Blelloch, Guy E.; Ferizovic, Daniel; Sun, Yihan (2016), "Just Join for Parallel Ordered Sets" (PDF), Simpósio sobre Algoritmos e Arquiteturas Paralelas, Proc. of 28th ACM Symp. Algoritmos e Arquiteturas Paralelas (SPAA 2016), ACM, pp. 253–264, arXiv:160,220, doi:10.1145/2935764.2935768, ISBN 978-1-4503-4210-0, S2CID 2897793.
- ^ Park, Heejin; Park, Kunsoo (2001). «Parallel algoritmos for red–black trees» (em inglês). Ciência da Computação Teórica. 262 (1–2): 415–435.10.1016/S0304-3975(00)00287-5.
Nosso algoritmo paralelo para construir uma árvore vermelha-preta de uma lista ordenada nNão. itens executados O(1)Não. tempo com nNão. processadores no CRCW PRAM e roda em O(log log n)Não. O(log log n)} tempo com n/log log n{displaystyle n/log log n} processadores no PRAM EREW.
- ^ Sanders, Peter (2019). Mehlhorn, Kurt; Dietzfelbinger, Martin; Dementiev, Roman (eds.). Algoritmos sequenciais e paralelos e estruturas de dados: A caixa de ferramentas básica. Springer eBooks. Cham: Springer. pp. 252–253. doi:10.1007/978-3-030-25209-0. ISBN 97830252090. S2CID 201692657.
- ^ Akhremtsev, Yaroslav; Sanders, Peter (2016). «Fast Parallel Operations on Search Trees» (em inglês). HiPC 2016, a 23a Conferência Internacional do IEEE sobre Computação de Alto Desempenho, Dados e Analytics, Hyderabad, Índia, dezembro, 19-22. IEEE, Piscataway (NJ): 291–300. arXiv:1510.0543. Bibcode:2015arXiv151005433A. ISBN 978-1-5090-5411-4.
- ^ Jájá, Joseph (1992). Uma introdução a algoritmos paralelos. Read, Mass. [u.a.]: Addison-Wesley. pp. 65–70. ISBN 0201548569. Zbl 0781.68009.
- ^ Missing (Série de TV canadense). A, W Network (Canadá); Lifetime (Estados Unidos).
- ^ Robert Sedgewick (2012). B-Trees. Coursera. 9:48 minutos.
Portanto, não só há alguma emoção nesse diálogo, mas também é tecnicamente correto que você muitas vezes não encontra com matemática na cultura popular da ciência da computação. Uma árvore vermelha-preta rastreia cada caminho simples de um nó para uma folha descendente com o mesmo número de nós negros que eles têm direito.
Contenido relacionado
Programa Estratégico Europeu de Pesquisa em Tecnologia da Informação
Dehidroepiandrosterona
Gráficos de Rede JPEG