Árvore AVL

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Árvore de pesquisa binária de auto-equilíbrio

Animação mostrando a inserção de vários elementos em uma árvore AVL. Inclui rotações esquerda, direita, esquerda e direita-esquerda.

Fig. 1: Árvore AVL com fatores de equilíbrio (verde)

Na ciência da computação, um Árvore AVL (nomeado após inventores ADelson...VElsky e Landis) é uma árvore de pesquisa binária deequilíbrio. Foi a primeira estrutura de dados a ser inventada. Em uma árvore AVL, as alturas dos dois subárvores de criança de qualquer nó diferem no máximo um; se em qualquer momento eles diferem por mais de um, reequilíbrio é feito para restaurar esta propriedade. Lookup, inserção e exclusão todos tomam $O(a) n)$ tempo em ambos os casos médios e piores, onde $n$ é o número de nós na árvore antes da operação. Inserções e exclusões podem exigir que a árvore seja reequilibrada por uma ou mais rotações de árvores.

A árvore AVL recebeu o nome de seus dois inventores soviéticos, Georgy Adelson-Velsky e Evgenii Landis, que a publicaram em seu artigo de 1962 "Um algoritmo para a organização da informação".

Árvores AVL são frequentemente comparadas com árvores vermelhas-pretas porque ambos suportam o mesmo conjunto de operações e tomam ${displaystyle {text{O}}(log n)}$ tempo para as operações básicas. Para aplicações intensivas em pesquisa, as árvores AVL são mais rápidas do que as árvores vermelhas-pretas porque são mais estritamente equilibradas. Semelhante a árvores vermelhas-pretas, as árvores AVL são balanceadas de altura. Ambos são, em geral, nem balanceados de peso nem $mu$ -equilibrado para qualquer ${displaystyle mu leq {tfrac {1}{2}}}$ ; isto é, nós de irmãos podem ter números enormemente diferentes de descendentes.

Definição

Fator de equilíbrio

Em uma árvore binária, o fator de equilíbrio de um nó X é definido como a diferença de altura

{displaystyle {text{BF}}(X):={text{Height}}({text{RightSubtree}}(X))-{text{Height}}({text{LeftSubtree}}(X))}

de suas duas subárvores filhas. Uma árvore binária é definida como uma árvore AVL se a invariante

{displaystyle {text{BF}}(X)in {{-1,0,1}}}

é válido para cada nó X na árvore.

Um nó X com $<math alttext="{displaystyle {text{BF}}(X)BF(X)<0{displaystyle {text{BF}}(X)<0} <img alt="{displaystyle {text{BF}}(X)$ é chamado de "left-heavy", um com $0}" xmlns="http://www.w3.org/1998/Math/MathML">BF(X)>0(X)>0} 0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c734f86938f93a517d974cb08080deabfba4f090" style="vertical-align: -0.838ex; width:11.214ex; height:2.843ex;"/>$ é chamado de "just-heavy", e um com ${displaystyle {text{BF}}(X)=0}$ às vezes é simplesmente chamado "equilibrado".

Propriedades

Os fatores de balanceamento podem ser atualizados conhecendo os fatores de balanceamento anteriores e a mudança de altura – não é necessário saber a altura absoluta. Para armazenar as informações de saldo AVL, dois bits por nó são suficientes.

A altura $h$ (contado como o número máximo de níveis) de uma árvore AVL com $n$ nodes reside no intervalo:

<math alttext="{displaystyle log _{2}(n+1)leq hlog2⁡ ⁡ (n+1)≤ ≤ h<logφ φ ⁡ ⁡ (n+2)+b){displaystyle log _{2}(n+1)leq h<log _{varphi }(n+2)+b}<img alt="{displaystyle log _{2}(n+1)leq h

Onde? ${displaystyle varphi:={tfrac {1+{sqrt {5}}}{2}}approx 1.618}$ é a proporção de ouro e ${displaystyle b:={frac {log _{2}5}{2log _{2}varphi }}-2approx ;-0.3277.}$ Isto é porque uma árvore AVL de altura $h$ contém pelo menos ${displaystyle F_{h}-1}$ nós onde ${displaystyle {F_{n}}_{nin mathbb {N} }}$ é a sequência de Fibonacci com os valores das sementes ${displaystyle F_{1}=F_{2}=1.}$

Operações

As operações somente leitura de uma árvore AVL envolvem a realização das mesmas ações que seriam realizadas em uma árvore de busca binária não balanceada, mas as modificações devem observar e restaurar o equilíbrio de altura das subárvores.

Pesquisando

A busca por uma chave específica em uma árvore AVL pode ser feita da mesma forma que em qualquer árvore de busca binária balanceada ou não balanceada. Para que a busca funcione efetivamente, ela deve empregar uma função de comparação que estabeleça uma ordem total (ou pelo menos uma pré-ordem total) no conjunto de chaves. O número de comparações necessárias para uma pesquisa bem-sucedida é limitado pela altura $h$ e para uma pesquisa malsucedida é muito próximo de $h$ , então ambos estão em $O(log n)$ .

Percurso

Como uma operação somente leitura, a travessia de uma árvore AVL funciona da mesma forma que em qualquer outra árvore binária. Explorar todos os nós $n$ da árvore visita cada link exatamente duas vezes: uma visita para baixo para entrar na subárvore enraizada por esse nó, outra visita para cima para sair dela subárvore do nó depois de explorá-lo.

Depois que um nó é encontrado em uma árvore AVL, o nó próximo ou anterior pode ser acessado em tempo constante amortizado. Algumas instâncias de exploração desses "próximos" os nós requerem percorrer até $h \propto log(n)$ links (particularmente ao navegar da folha mais à direita da raiz&# 39; da subárvore esquerda para a raiz ou da raiz para a folha mais à esquerda da subárvore direita da raiz; na árvore AVL da figura 1, navegar do nó P para o próximo nó à direita Q leva 3 passos). Como existem $n -1$ links em qualquer árvore, o custo amortizado é $2\times(n -1)/ n$ , ou aproximadamente 2.

Inserir

Ao inserir um nó em uma árvore AVL, você inicialmente segue o mesmo processo de inserção em uma árvore de pesquisa binária. Se a árvore estiver vazia, o nó é inserido como a raiz da árvore. Se a árvore não estiver vazia, descemos pela raiz e recursivamente descemos a árvore procurando o local para inserir o novo nó. Esta travessia é guiada pela função de comparação. Nesse caso, o nó sempre substitui uma referência NULL (esquerda ou direita) de um nó externo na árvore, ou seja, o nó é feito filho esquerdo ou filho direito do nó externo.

Após esta inserção, se uma árvore se tornar desbalanceada, apenas os ancestrais do novo nó inserido serão desbalanceados. Isso ocorre porque apenas esses nós têm suas subárvores alteradas. Portanto, é necessário verificar a consistência de cada um dos ancestrais do nó com os invariantes das árvores AVL: isso é chamado de "retraçar". Isso é obtido considerando o fator de equilíbrio de cada nó.

Como com uma única inserção a altura de uma subárvore AVL não pode aumentar em mais de um, o fator de equilíbrio temporário de um nó após uma inserção estará no intervalo [–2,+2 ]. Para cada nó verificado, se o fator de balanceamento temporário permanecer na faixa de –1 a +1, apenas uma atualização do fator de balanceamento e nenhuma rotação será necessária. No entanto, se o fator de balanceamento temporário for ±2, a subárvore com raiz neste nó é AVL desbalanceada e uma rotação é necessária. Com a inserção como mostra o código abaixo, a rotação adequada imediatamente reequilibra perfeitamente a árvore.

Na figura 1, ao inserir o novo nó Z como filho do nó X, a altura dessa subárvore Z aumenta de 0 para 1.

Invariante do laço de retração para uma inserção

A altura da subárvore enraizada por Z aumentou em 1. Já está no formato AVL.

Exemplo de código para uma operação de inserção
para (X = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = pai(Z.); X ! Null; X = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = pai(Z.) ( // Loop (possivelmente até a raiz) // BF(X) tem de ser atualizado: se (Z. - Sim. Certo.(X) ( // O subárvore direito aumenta se (BF(X) > 0) ( // X é direito pesado // ==> o BF temporário (X) == + // ==> reequilíbrio é necessário. G = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = pai(X); // Salvar pai de X em torno de rotações se (BF(Z.) < 0) // Caso Esquerda Direita (ver figura 3) N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = rotativo_LightLeft(X, Z.); // Rotação dupla: Direita (Z) então Esquerda(X) mais // Caso direito (ver figura 2) N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = rotativo_ Esquerda(X, Z.); // Rotação única Esquerda(X) // Após a rotação adapte a ligação pai ? mais ( se (BF(X) < 0) ( BF(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 0; // O aumento de altura de Z é absorvido em X. pausa; // Deixe o laço ? BF(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = +1; Z. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = X; // Altura(Z) aumenta em 1 continuar; ? ? mais ( // Z == left_child(X): o subárvore esquerdo aumenta se (BF(X) < 0) ( // X é de esquerda // ==> o BF temporário (X) == -2 // ==> reequilíbrio é necessário. G = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = pai(X); // Salvar pai de X em torno de rotações se (BF(Z.) > 0) // Caso direito esquerdo N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = rotativo_ Esquerda(X, Z.); // Rotação dupla: Esquerda(Z) então Direita(X) mais // Caso de esquerda N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = rotativo_ Certo.(X, Z.); // Rotação única Direita (X) // Após a rotação adapte a ligação pai ? mais ( se (BF(X) > 0) ( BF(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 0; // O aumento de altura de Z é absorvido em X. pausa; // Deixe o laço ? BF(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = -1; Z. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = X; // Altura(Z) aumenta em 1 continuar; ? ? // Depois de uma rotação adapte o link pai: // N é a nova raiz do subárvore rotativo // Altura não muda: Altura (N) == Altura velha (X) pai(N) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = G; se (G ! Null) ( se (X - Sim. esquerda_criança(G) esquerda_criança(G) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = N; mais Certo.(G) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = N; ? mais árvore- Sim.raiz raiz = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = N; // N é a nova raiz da árvore total pausa; // Não há queda thru, apenas ruptura; ou continuar;?// A menos que o loop seja deixado através de ruptura, a altura da árvore total aumenta em 1.

Exemplo de código para uma operação de inserção

para (X = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = pai(Z.); X ! Null; X = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = pai(Z.) ( // Loop (possivelmente até a raiz) // BF(X) tem de ser atualizado: se (Z. - Sim. Certo.(X) ( // O subárvore direito aumenta se (BF(X) > 0) ( // X é direito pesado // ==> o BF temporário (X) == + // ==> reequilíbrio é necessário. G = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = pai(X); // Salvar pai de X em torno de rotações se (BF(Z.) < 0) // Caso Esquerda Direita (ver figura 3) N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = rotativo_LightLeft(X, Z.); // Rotação dupla: Direita (Z) então Esquerda(X) mais // Caso direito (ver figura 2) N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = rotativo_ Esquerda(X, Z.); // Rotação única Esquerda(X) // Após a rotação adapte a ligação pai ? mais ( se (BF(X) < 0) ( BF(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 0; // O aumento de altura de Z é absorvido em X. pausa; // Deixe o laço ? BF(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = +1; Z. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = X; // Altura(Z) aumenta em 1 continuar; ? ? mais ( // Z == left_child(X): o subárvore esquerdo aumenta se (BF(X) < 0) ( // X é de esquerda // ==> o BF temporário (X) == -2 // ==> reequilíbrio é necessário. G = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = pai(X); // Salvar pai de X em torno de rotações se (BF(Z.) > 0) // Caso direito esquerdo N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = rotativo_ Esquerda(X, Z.); // Rotação dupla: Esquerda(Z) então Direita(X) mais // Caso de esquerda N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = rotativo_ Certo.(X, Z.); // Rotação única Direita (X) // Após a rotação adapte a ligação pai ? mais ( se (BF(X) > 0) ( BF(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 0; // O aumento de altura de Z é absorvido em X. pausa; // Deixe o laço ? BF(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = -1; Z. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = X; // Altura(Z) aumenta em 1 continuar; ? ? // Depois de uma rotação adapte o link pai: // N é a nova raiz do subárvore rotativo // Altura não muda: Altura (N) == Altura velha (X) pai(N) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = G; se (G ! Null) ( se (X - Sim. esquerda_criança(G) esquerda_criança(G) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = N; mais Certo.(G) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = N; ? mais árvore- Sim.raiz raiz = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = N; // N é a nova raiz da árvore total pausa; // Não há queda thru, apenas ruptura; ou continuar;?// A menos que o loop seja deixado através de ruptura, a altura da árvore total aumenta em 1.

Para atualizar os fatores de balanceamento de todos os nós, primeiro observe que todos os nós que requerem correção estão do filho para o pai ao longo do caminho da folha inserida. Se o procedimento acima for aplicado aos nós ao longo deste caminho, começando pela folha, então cada nó na árvore terá novamente um fator de equilíbrio de -1, 0 ou 1.

O retrocesso pode parar se o fator de equilíbrio se tornar 0, o que implica que a altura dessa subárvore permanece inalterada.

Se o fator de equilíbrio se tornar ±1, a altura da subárvore aumenta em um e o retraço precisa continuar.

Se o fator de equilíbrio tornar-se temporariamente ±2, isso deve ser reparado por uma rotação apropriada após a qual a subárvore tem a mesma altura que antes (e sua raiz o fator de equilíbrio 0).

O tempo necessário é $O(log n)$ para pesquisa, mais um máximo de $O(log n)$ refazendo os níveis ( $O(1)$ em média) no caminho de volta à raiz, para que a operação possa ser concluída em $O(log n)$ tempo.

Excluir

As etapas preliminares para excluir um nó são descritas na seção Árvore de pesquisa binária#Exclusão. Lá, a exclusão efetiva do nó sujeito ou do nó substituto diminui a altura da árvore filho correspondente de 1 para 0 ou de 2 para 1, se esse nó tiver um filho.

A partir desta subárvore, é necessário verificar a consistência de cada um dos ancestrais com os invariantes das árvores AVL. Isso é chamado de "retraçar".

Como com uma única exclusão a altura de uma subárvore AVL não pode diminuir em mais de um, o fator de equilíbrio temporário de um nó estará na faixa de -2 a +2. Se o fator de balanceamento permanecer na faixa de -1 a +1, ele pode ser ajustado de acordo com as regras AVL. Se for ±2, então a subárvore está desbalanceada e precisa ser rotacionada. (Ao contrário da inserção em que uma rotação sempre equilibra a árvore, após a exclusão, pode haver BF(Z) ≠ 0 (consulte as figuras 2 e 3), de modo que, após a rotação simples ou dupla apropriada, a altura da subárvore rebalanceada diminui em um significado que a árvore deve ser rebalanceada novamente no próximo nível superior.) Os vários casos de rotações são descritos na seção Rebalanceamento.

Invariante do loop de retificação para uma eliminação

A altura da subárvore enraizada por N diminuiu em 1. Ela já está no formato AVL.

Exemplo de código para uma operação de exclusão
para (X = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = pai(N); X ! Null; X = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = G) ( // Loop (possivelmente até a raiz) G = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = pai(X); // Salvar pai de X em torno de rotações // BF(X) ainda não foi atualizado! se (N - Sim. esquerda_criança(X) ( // o subárvore esquerdo diminui se (BF(X) > 0) ( // X é direito pesado // ==> o BF temporário (X) == + // ==> reequilíbrio é necessário. Z. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = Certo.(X); // Sibling de N (maior por 2) b) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = BF(Z.); se (b) < 0) // Caso Esquerda Direita (ver figura 3) N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = rotativo_LightLeft(X, Z.); // Rotação dupla: Direita (Z) então Esquerda(X) mais // Caso direito (ver figura 2) N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = rotativo_ Esquerda(X, Z.); // Rotação única Esquerda(X) // Após a rotação adapte a ligação pai ? mais ( se (BF(X) - Sim. 0) ( BF(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = +1; // A diminuição da altura de N é absorvida em X. pausa; // Deixe o laço ? N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = X; BF(N) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 0; // Altura (N) diminui em 1 continuar; ? ? mais ( // (N == right_child(X)): O subárvore direito diminui se (BF(X) < 0) ( // X é de esquerda // ==> o BF temporário (X) == -2 // ==> reequilíbrio é necessário. Z. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = esquerda_criança(X); // Sibling de N (maior por 2) b) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = BF(Z.); se (b) > 0) // Caso direito esquerdo N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = rotativo_ Esquerda(X, Z.); // Rotação dupla: Esquerda(Z) então Direita(X) mais // Caso de esquerda N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = rotativo_ Certo.(X, Z.); // Rotação única Direita (X) // Após a rotação adapte a ligação pai ? mais ( se (BF(X) - Sim. 0) ( BF(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = -1; // A diminuição da altura de N é absorvida em X. pausa; // Deixe o laço ? N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = X; BF(N) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 0; // Altura (N) diminui em 1 continuar; ? ? // Depois de uma rotação adapte o link pai: // N é a nova raiz do subárvore rotativo pai(N) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = G; se (G ! Null) ( se (X - Sim. esquerda_criança(G) esquerda_criança(G) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = N; mais Certo.(G) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = N; ? mais árvore- Sim.raiz raiz = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = N; // N é a nova raiz da árvore total se (b) - Sim. 0) pausa; // A altura não muda: Deixe o laço // Altura (N) diminui por 1 (= Altura velha (X)-1)?- Sim. 0) a altura da árvore total diminui por 1.

Exemplo de código para uma operação de exclusão

para (X = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = pai(N); X ! Null; X = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = G) ( // Loop (possivelmente até a raiz) G = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = pai(X); // Salvar pai de X em torno de rotações // BF(X) ainda não foi atualizado! se (N - Sim. esquerda_criança(X) ( // o subárvore esquerdo diminui se (BF(X) > 0) ( // X é direito pesado // ==> o BF temporário (X) == + // ==> reequilíbrio é necessário. Z. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = Certo.(X); // Sibling de N (maior por 2) b) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = BF(Z.); se (b) < 0) // Caso Esquerda Direita (ver figura 3) N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = rotativo_LightLeft(X, Z.); // Rotação dupla: Direita (Z) então Esquerda(X) mais // Caso direito (ver figura 2) N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = rotativo_ Esquerda(X, Z.); // Rotação única Esquerda(X) // Após a rotação adapte a ligação pai ? mais ( se (BF(X) - Sim. 0) ( BF(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = +1; // A diminuição da altura de N é absorvida em X. pausa; // Deixe o laço ? N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = X; BF(N) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 0; // Altura (N) diminui em 1 continuar; ? ? mais ( // (N == right_child(X)): O subárvore direito diminui se (BF(X) < 0) ( // X é de esquerda // ==> o BF temporário (X) == -2 // ==> reequilíbrio é necessário. Z. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = esquerda_criança(X); // Sibling de N (maior por 2) b) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = BF(Z.); se (b) > 0) // Caso direito esquerdo N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = rotativo_ Esquerda(X, Z.); // Rotação dupla: Esquerda(Z) então Direita(X) mais // Caso de esquerda N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = rotativo_ Certo.(X, Z.); // Rotação única Direita (X) // Após a rotação adapte a ligação pai ? mais ( se (BF(X) - Sim. 0) ( BF(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = -1; // A diminuição da altura de N é absorvida em X. pausa; // Deixe o laço ? N = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = X; BF(N) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 0; // Altura (N) diminui em 1 continuar; ? ? // Depois de uma rotação adapte o link pai: // N é a nova raiz do subárvore rotativo pai(N) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = G; se (G ! Null) ( se (X - Sim. esquerda_criança(G) esquerda_criança(G) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = N; mais Certo.(G) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = N; ? mais árvore- Sim.raiz raiz = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = N; // N é a nova raiz da árvore total  se (b) - Sim. 0) pausa; // A altura não muda: Deixe o laço  // Altura (N) diminui por 1 (= Altura velha (X)-1)?- Sim. 0) a altura da árvore total diminui por 1.

O retrocesso pode parar se o fator de equilíbrio se tornar ±1 (deve ser 0), o que significa que a altura dessa subárvore permanece inalterada.

Se o fator de equilíbrio se tornar 0 (deve ter sido ±1), a altura da subárvore diminui em um e o retraço precisa continuar.

Se o fator de balanceamento se tornar temporariamente ±2, isso deve ser reparado por uma rotação apropriada. Depende do fator de equilíbrio do irmão Z (a árvore filho mais alta na figura 2) se a altura da subárvore diminui em um – e a retração precisa continuar – ou não muda (se Z tem o fator de equilíbrio 0) e toda a árvore está em formato AVL.

Definir operações e operações em massa

Além das operações de inserção, exclusão e pesquisa de elemento único, várias operações de conjunto foram definidas nas árvores AVL: união, interseção e diferença de conjunto. Em seguida, operações em massa rápidas em inserções ou exclusões podem ser implementadas com base nessas funções definidas. Essas operações definidas dependem de duas operações auxiliares, Split e Join. Com as novas operações, a implementação de árvores AVL pode ser mais eficiente e altamente paralelizável.

A função Join em duas árvores AVL $t 1$ e $t 2$ e uma chave $k$ retornará uma árvore contendo todos os elementos em $t 1$ , $t 2$ , bem como $k$ . Requer que $k$ seja maior que todas as chaves em $t 1$ e menor que todas as chaves em $t 2$ . Se as duas árvores diferirem em altura no máximo um, Junte-se simplesmente crie um novo nó com a subárvore esquerda $t 1$ , raiz $k$ e subárvore direita $t 2$ . Caso contrário, suponha que $t 1$ seja maior que $t 2$ para mais de um (o outro caso é simétrico). Join segue a espinha direita de $t 1$ até um nó $c$ que é balanceado com $t 2$ . Neste ponto, um novo nó com o filho esquerdo $c$ , raiz $k$ e o filho direito $t 2$ é criado para substituir c. O novo nó satisfaz a invariante AVL e sua altura é um maior que $c$ . O aumento da altura pode aumentar a altura de seus ancestrais, possivelmente invalidando a invariante AVL desses nós. Isso pode ser corrigido com uma rotação dupla se for inválido no pai ou uma única rotação à esquerda se for inválido mais alto na árvore, em ambos os casos restaurando a altura para quaisquer outros nós ancestrais. Join exigirá, portanto, no máximo duas rotações. O custo desta função é a diferença das alturas entre as duas árvores de entrada.

Implementação Pseudocode para o algoritmo de adesão
função Inscreva-se emRightAVL (T_L, k, T_R) (l, k', c) = expor (T_L) se (Altura(c) <= Altura (T)_R)+1) T' = Node(c, k, T)_R) se (Altura (T) <= Altura (l)+1) então retorno Node(l, k', T') mais retorno rotateLeft(Node(l, k', rotateRight(T'))))) mais T' = JoinRightAVL(c, k, T_R) T'' = Node (l, k', T') se (Altura (T) <= Altura (l)+1) retorno T mais retorno rotateLeft(T') função Junte-se aLeftAVL (T_L, k, T_R) /* simétrico para JoinRightAVL * função Participar (T_L, k, T_R) se (Altura (T)_L) Altura (T_R)+1) retorno Inscreva-se emRightAVL (T_L, k, T_R) se (Altura (T)_R) Altura (T_L)+1) retorno Junte-se aLeftAVL (T_L, k, T_R) retorno Node (T)_L, k, T_R) Aqui Altura (v) é a altura de um subárvore (nodo) $v$ . (l,k,r) = exp.(v) extratos $v$ A criança esquerda $Eu...$ , a chave $k$ de $v$ A raiz, e a criança certa $R$ . Node(l,k,r) significa criar um nó de criança esquerda $Eu...$ , chave $k$ , e criança certa $R$ .

Implementação Pseudocode para o algoritmo de adesão

função Inscreva-se emRightAVL (T_L, k, T_R)
(l, k', c) = expor (T_L)
 se (Altura(c) <= Altura (T)_R)+1)
T' = Node(c, k, T)_R)
se (Altura (T) <= Altura (l)+1) então retorno Node(l, k', T')
mais retorno rotateLeft(Node(l, k', rotateRight(T')))))
 mais T' = JoinRightAVL(c, k, T_R)
T'' = Node (l, k', T')
 se (Altura (T) <= Altura (l)+1) retorno T
 mais retorno rotateLeft(T')

função Junte-se aLeftAVL (T_L, k, T_R)
/* simétrico para JoinRightAVL *

função Participar (T_L, k, T_R)
 se (Altura (T)_L) Altura (T_R)+1) retorno Inscreva-se emRightAVL (T_L, k, T_R)
 se (Altura (T)_R) Altura (T_L)+1) retorno Junte-se aLeftAVL (T_L, k, T_R)
 retorno Node (T)_L, k, T_R)

Aqui Altura (v) é a altura de um subárvore (nodo) $v$ . (l,k,r) = exp.(v) extratos $v$ A criança esquerda $Eu...$ , a chave $k$ de $v$ A raiz, e a criança certa $R$ . Node(l,k,r) significa criar um nó de criança esquerda $Eu...$ , chave $k$ , e criança certa $R$ .

Para dividir uma árvore AVL em duas árvores menores, as menores que a chave $k$ e as maiores que a chave $k$ , primeiro desenhe um caminho a partir da raiz inserindo $k$ no AVL. Após esta inserção, todos os valores menores que $k$ serão encontrados à esquerda do caminho, e todos os valores maiores que $k$ será encontrado à direita. Ao aplicar Join, todas as subárvores do lado esquerdo são mescladas de baixo para cima usando chaves no caminho como nós intermediários de baixo para cima para formar a árvore esquerda, e a parte direita é assimétrica. O custo de Split é $O(log n)$ , ordem da altura da árvore.

Implementação de Pseudocode para o algoritmo Split
função Split (T, k) se (T = nil) retorno (nil, falso, nil) (L,m,R) = expor(T) se (k = m) retorno (L, verdadeiro, R) se (k<m) (L',b,R') = Split (L,k) retorno (L', b, Join(R', m, R) se (k>m) (L',b,R') = Split (R, k) retorno (Join(L, m, L'), b, R')

Implementação de Pseudocode para o algoritmo Split

função Split (T, k)
 se (T = nil) retorno (nil, falso, nil)
(L,m,R) = expor(T)
 se (k = m) retorno (L, verdadeiro, R)
 se (k<m)
(L',b,R') = Split (L,k)
 retorno (L', b, Join(R', m, R)
 se (k>m)
(L',b,R') = Split (R, k)
 retorno (Join(L, m, L'), b, R')

A união de duas árvores AVL $t 1$ e $t 2$ representando os conjuntos $A$ e $B$ , é um AVL $t$ que representa $A \cup B$ .

Implementação de Pseudocode para o algoritmo da União
função União Europeia₁,₂: se)₁ - Não. retorno)₂ se)₂ - Não. retorno)₁Não._<, b, t_>) = Split (t)₂,₁.root) retorno Junte-se (União (esquerda)₁),_<),₁.root, Union(right(t)₁),_>) Toma. Divisão é presumido para devolver duas árvores: uma segurando as chaves menos sua chave de entrada, uma segurando as chaves maiores. (O algoritmo é não-destrutivo, mas uma versão destrutiva no local também existe.)

Implementação de Pseudocode para o algoritmo da União

função União Europeia₁,₂:
 se)₁ - Não.
 retorno)₂ se)₂ - Não.
 retorno)₁Não._<, b, t_>) = Split (t)₂,₁.root)
 retorno Junte-se (União (esquerda)₁),_<),₁.root, Union(right(t)₁),_>)

Toma. Divisão é presumido para devolver duas árvores: uma segurando as chaves menos sua chave de entrada, uma segurando as chaves maiores. (O algoritmo é não-destrutivo, mas uma versão destrutiva no local também existe.)

O algoritmo para interseção ou diferença é semelhante, mas requer a rotina auxiliar Join2 que é igual a Join, mas sem a chave do meio. Com base nas novas funções de união, interseção ou diferença, uma chave ou várias chaves podem ser inseridas ou excluídas da árvore AVL. Como Split chama Join, mas não lida diretamente com os critérios de balanceamento das árvores AVL, tal implementação é geralmente chamada de implementação "baseada em junção" implementação.

A complexidade de cada união, interseção e diferença é ${displaystyle {text{O}}left(mlog left({n over m}+1right)right)}$ para árvores AVL de tamanhos $m$ e ${displaystyle n;(geq m)}$ . Mais importante, uma vez que as chamadas recursivas para união, interseção ou diferença são independentes umas das outras, elas podem ser executadas em paralelo com uma profundidade paralela ${displaystyle {text{O}}(log mlog n)}$ . Quando $m=1$ , a implementação baseada na união tem o mesmo DAG computacional como inserção e exclusão de elementos únicos.

Reequilíbrio

Se durante uma operação de modificação a diferença de altura entre duas subárvores filhas mudar, isso pode, desde que seja < 2, ser refletido por uma adaptação das informações de saldo no pai. Durante as operações de inserção e exclusão, pode surgir uma diferença de altura (temporária) de 2, o que significa que a subárvore pai deve ser "rebalanceada". As ferramentas de reparo fornecidas são as chamadas rotações de árvore, porque elas movem as chaves apenas "verticalmente", de modo que a sequência ("horizontal") em ordem das chaves seja totalmente preservada (o que é essencial para uma árvore de pesquisa binária).

Seja X o nó que possui um fator de balanceamento (temporário) de -2 ou +2. Sua subárvore esquerda ou direita foi modificada. Seja Z o filho mais alto (ver figuras 2 e 3). Observe que ambas as crianças estão em formato AVL pela hipótese de indução.

No caso de inserção, esta inserção aconteceu com um dos filhos de Z de forma que a altura de Z aumentou. Em caso de exclusão, esta exclusão ocorreu com o irmão t₁ de Z de forma que a altura de t₁' já sendo menor diminuiu. (Este é o único caso em que o fator de equilíbrio de Z também pode ser 0.)

Existem quatro variantes possíveis da violação:

Certo.	? Z é um Certo.	criança de seu pai X e BF(Z) ≥ 0
Esquerda esquerda	? Z é um esquerda	criança de seu pai X e BF(Z) ≤ 0
Esquerda direita	? Z é um Certo.	filho de seu pai X e BF(Z) < 0
Esquerda direita	? Z é um esquerda	filho de seu pai X e BF(Z) > 0

E o rebalanceamento é feito de forma diferente:

Certo.	? X é reequilibrado com um	simples	rotação `rotate_Left`	(ver figura 2)
Esquerda esquerda	? X é reequilibrado com um	simples	rotação `rotate_Right`	(imagem do espelho da figura 2)
Esquerda direita	? X é reequilibrado com um	duplo	rotação `rotate_RightLeft`	(ver figura 3)
Esquerda direita	? X é reequilibrado com um	duplo	rotação `rotate_LeftRight`	(imagem do espelho da figura 3)

Assim, as situações são denotadas como C B, onde C (= direção da criança) e B (= saldo) vêm do conjunto { Esquerda, Direita } com Direita:= −Esquerda. A violação de equilíbrio do caso C == B é reparado por uma simples rotação rotate_(−C), enquanto o caso C != B é reparado por uma rotação dupla rotate_ CB.

O custo de uma rotação, simples ou dupla, é constante.

Rotação simples

A Figura 2 mostra uma situação de Right Right. Em sua metade superior, o nó X possui duas árvores filhas com um fator de equilíbrio de +2. Além disso, o filho interno t₂₃ de Z (isto é, filho esquerdo quando Z é filho direito, ou filho direito quando Z é filho esquerdo) não é maior que seu irmão t₄. Isso pode acontecer por um aumento de altura da subárvore t₄ ou por uma diminuição da altura da subárvore t₁. Neste último caso, também pode ocorrer a situação pálida em que t₂₃ tem a mesma altura que t₄.

O resultado da rotação à esquerda é mostrado na metade inferior da figura. Três links (bordas grossas na figura 2) e dois fatores de balanceamento devem ser atualizados.

Como mostra a figura, antes de uma inserção, a camada de folha estava no nível h+1, temporariamente no nível h+2 e após a rotação novamente no nível h+1. No caso de uma exclusão, a camada folha estava no nível h+2, onde está novamente, quando t₂₃ e t₄ tinham a mesma altura. Caso contrário, a camada de folha atinge o nível h+1, de modo que a altura da árvore girada diminui.

Fig. 2: rotação simples
rotativo_ Esquerda(X,Z.)

Snippet de código de uma rotação esquerda simples

Entrada:	X = raiz de subárvore para ser esquerda rotativa
	Z = criança direita de X, Z é direito pesado
	com altura = $Altura (LeftSubtree($ X $)+2$
Resultado:	nova raiz de subárvore reequilibrada

Node *rotativo_ Esquerda(Node *X, Node *Z.) ( // Z é 2 mais alto do que seu irmão T23 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = esquerda_criança(Z.); // Criança interna de Z Certo.(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = T23; se (T23 ! Null) pai(T23) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = X; esquerda_criança(Z.) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = X; pai(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = Z.; // 1o caso, BF(Z) == 0, // só acontece com exclusão, não inserção: se (BF(Z.) - Sim. 0) ( // t23 tem sido da mesma altura que t4 BF(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = +1; // t23 agora maior BF(Z.) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = –1; // t4 agora inferior a X ? mais ( // 2o caso acontece com inserção ou exclusão: BF(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 0; BF(Z.) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 0; ? retorno Z.; // retornar nova raiz do subárvore rotativo?

Rotação dupla

A Figura 3 mostra uma situação Direita Esquerda. Em seu terço superior, o nó X possui duas árvores filhas com um fator de equilíbrio de +2. Mas, ao contrário da figura 2, a criança interna Y de Z é maior que seu irmão t₄. Isso pode ocorrer pela inserção do próprio Y ou pelo aumento da altura de uma de suas subárvores t₂ ou t₃ (com a consequência de terem alturas diferentes) ou por uma diminuição da altura da subárvore t₁. Neste último caso, também pode ocorrer que t₂ e t₃ tenham a mesma altura.

O resultado da primeira rotação, a direita, é mostrado no terço central da figura. (Com relação aos fatores de equilíbrio, esta rotação não é do mesmo tipo que as outras rotações únicas AVL, porque a diferença de altura entre Y e t₄ é apenas 1.) O resultado da esquerda final rotação é mostrada no terço inferior da figura. Cinco links (bordas grossas na figura 3) e três fatores de equilíbrio devem ser atualizados.

Como mostra a figura, antes de uma inserção, a camada de folha estava no nível h+1, temporariamente no nível h+2 e após a dupla rotação novamente no nível h+1. Em caso de deleção, a camada folha estava no nível h+2 e após a dupla rotação está no nível h+1, de forma que a altura da árvore rotacionada diminui.

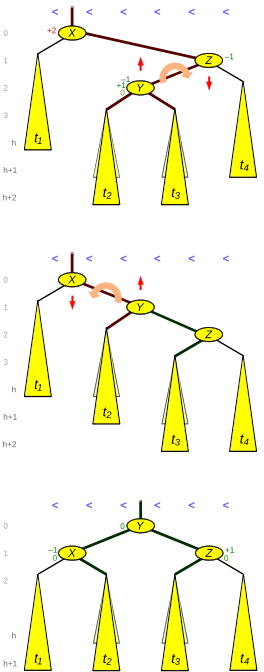
Fig. 3: Rotação dupla rotativo_LightLeft(X,Z.)
= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = rotativo_ Certo. ao redor Z. seguido por
rotativo_ Esquerda ao redor X

Código snippet de uma rotação dupla direita-esquerda

Entrada:	X = raiz de subárvore a ser girada
	Z = sua criança direita, esquerda-pesada
	com altura = $Altura (LeftSubtree($ X $)+2$
Resultado:	nova raiz de subárvore reequilibrada

Node *rotativo_LightLeft(Node *X, Node *Z.) ( // Z é 2 mais alto do que seu irmão Y = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = esquerda_criança(Z.); // Criança interna de Z // Y é por 1 mais alto do que o irmão T3 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = Certo.(Y); esquerda_criança(Z.) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = T3; se (T3 ! Null) pai(T3) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = Z.; Certo.(Y) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = Z.; pai(Z.) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = Y; T2 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = esquerda_criança(Y); Certo.(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = T2; se (T2 ! Null) pai(T2) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = X; esquerda_criança(Y) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = X; pai(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = Y; // 1o caso, BF(Y) == 0, // só acontece com exclusão, não inserção: se (BF(Y) - Sim. 0) ( BF(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 0; BF(Z.) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 0; ? mais // outros casos acontecem com inserção ou exclusão: se (BF(Y) > 0) ( // t3 foi maior BF(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = –1; // t1 agora maior BF(Z.) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 0; ? mais ( // t2 foi maior BF(X) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 0; BF(Z.) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = +1; // t4 agora maior ? BF(Y) = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 0; retorno Y; // retornar nova raiz do subárvore rotativo?

Comparação com outras estruturas

As árvores AVL e as árvores vermelho-preto (RB) são árvores binárias de busca autobalanceadas e estão relacionadas matematicamente. De fato, toda árvore AVL pode ser colorida em vermelho-preto, mas há árvores RB que não são balanceadas com AVL. Para manter o AVL (ou invariantes da árvore RB), as rotações desempenham um papel importante. No pior caso, mesmo sem rotações, as inserções ou exclusões de AVL ou RB requerem $O(log n)$ inspeções e/ou atualizações dos fatores de balanceamento de AVL (ou cores RB). As inserções e exclusões de RB e as inserções de AVL requerem de zero a três rotações recursivas de cauda e são executadas em tempo $O(1)$ amortizado, portanto, igualmente constante em média. Exclusões de AVL que exigem rotações $O(log n)$ no pior caso também são $O(1)$ na média. As árvores RB requerem o armazenamento de um bit de informação (a cor) em cada nó, enquanto as árvores AVL usam principalmente dois bits para o fator de equilíbrio, embora, quando armazenado nos filhos, um bit com significado «menor que irmão» seja suficiente. A maior diferença entre as duas estruturas de dados é o limite de altura.

Para uma árvore de tamanho $n \geq 1$

a altura de uma árvore AVL é no máximo
$<math alttext="{displaystyle {begin{array}{ll}h&leqq ;clog _{2}(n+d)+b\&h≦ ≦ clog2⁡ ⁡ (n+D)+b)<clog2⁡ ⁡ (n+2)+b){displaystyle {begin{array}{ll}h&leqq ;clog _{2}(n+d)+b&<;clog _{2}(n+2)+bend{array}}}<img alt="{displaystyle {begin{array}{ll}h&leqq ;clog _{2}(n+d)+b\&$

Onde?

{displaystyle varphi:={tfrac {1+{sqrt {5}}}{2}}approx 1.618}

a relação de ouro,

{displaystyle c:={tfrac {1}{log _{2}varphi }}approx 1.440,}

{displaystyle b:={tfrac {c}{2}}log _{2}5-2approx ;-0.328,}

{displaystyle d:=1+{tfrac {1}{varphi ^{4}{sqrt {5}}}}approx 1.065}

a altura de uma árvore RB é no máximo
${displaystyle {begin{array}{ll}h&leqq ;2log _{2}(n+1)end{array}}}$ .

As árvores AVL são mais rigidamente balanceadas do que as árvores RB com uma relação assintótica AVL/RB ≈0,720 das alturas máximas. Para inserções e deleções, Ben Pfaff mostra em 79 medições uma relação de AVL/RB entre 0,677 e 1,077 com mediana ≈0,947 e média geométrica ≈0,910.

Contenido relacionado

Más resultados...