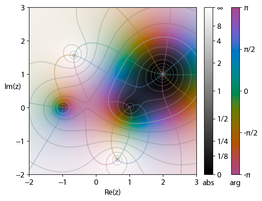
Análise complexa

Análise complexa, tradicionalmente conhecida como teoria das funções de uma variável complexa, é o ramo da análise matemática que investiga funções de números complexos. É útil em muitos ramos da matemática, incluindo geometria algébrica, teoria dos números, combinatória analítica, matemática aplicada; bem como na física, incluindo os ramos da hidrodinâmica, termodinâmica e particularmente da mecânica quântica. Por extensão, o uso de análise complexa também tem aplicações em campos de engenharia como nuclear, aeroespacial, mecânica e elétrica.

Como uma função diferenciável de uma variável complexa é igual à sua série de Taylor (isto é, é analítica), a análise complexa está particularmente preocupada com funções analíticas de uma variável complexa (isto é, funções holomórficas).

História

Augustin-Louis Cauchy, um dos fundadores da análise complexa

A análise complexa é um dos ramos clássicos da matemática, com raízes no século 18 e um pouco antes. Matemáticos importantes associados a números complexos incluem Euler, Gauss, Riemann, Cauchy, Gösta Mittag-Leffler, Weierstrass e muitos outros no século XX. A análise complexa, em particular a teoria dos mapeamentos conformes, tem muitas aplicações físicas e também é usada em toda a teoria analítica dos números. Nos tempos modernos, tornou-se muito popular por meio de um novo impulso da dinâmica complexa e das imagens de fractais produzidas por iterações de funções holomórficas. Outra aplicação importante da análise complexa é na teoria das cordas, que examina invariantes conformes na teoria quântica de campos.

Funções complexas

Uma função exponencial Aⁿ de uma variável discreta (integer) n, semelhante à progressão geométrica

Uma função complexa é uma função de números complexos para números complexos. Em outras palavras, é uma função que tem um subconjunto dos números complexos como domínio e os números complexos como contradomínio. As funções complexas geralmente devem ter um domínio que contém um subconjunto aberto não vazio do plano complexo.

Para qualquer função complexa, os valores $Não.$ do domínio e suas imagens $Não.$ na faixa pode ser separada em partes reais e imaginárias:

$(x+iy)=u(x,y)+iv(x,y),}$

Onde? ${displaystyle x,y,u(x,y),v(x,y)}$ são todos reais.

Em outras palavras, uma função complexa ${displaystyle f:mathbb] {C} to mathbb Não.$ pode ser decomposto

${displaystyle u:mathbb {R} ^{2}to mathbb Não.$ e ${displaystyle quad v:mathbb {R} ^{2}to mathbb (R)$

ou seja, em duas funções reais ($Não.$, $Não.$) de duas variáveis reais ($Não.$, $- Sim.$).

Da mesma forma, qualquer função de valor complexo f em um conjunto arbitrário X (é isomorfo para, e, portanto, nesse sentido, ele) pode ser considerado como um par ordenado de duas funções de valor real: (Re) fIm f) ou, alternativamente, como uma função de valor vetorial X para dentro ${displaystyle mathbb {R} ^{2}.}$

Algumas propriedades de funções de valor complexo (como continuidade) nada mais são do que as propriedades correspondentes de funções de valor vetorial de duas variáveis reais. Outros conceitos de análise complexa, como diferenciabilidade, são generalizações diretas de conceitos semelhantes para funções reais, mas podem ter propriedades muito diferentes. Em particular, toda função complexa diferenciável é analítica (veja a próxima seção), e duas funções diferenciáveis que são iguais na vizinhança de um ponto são iguais na interseção de seus domínios (se os domínios estiverem conectados). A última propriedade é a base do princípio da continuação analítica que permite estender cada função analítica real de uma maneira única para obter uma função analítica complexa cujo domínio é todo o plano complexo com um número finito de arcos de curva removidos. Muitas funções complexas básicas e especiais são definidas dessa maneira, incluindo a função exponencial complexa, funções logarítmicas complexas e funções trigonométricas.

Funções holomórficas

Funções complexas que são diferenciadas em cada ponto de um subconjunto aberto $Não. - Sim.$ do plano complexo dizem ser holomorfo em $Não. - Sim.$. No contexto da análise complexa, o derivado de $Não.$ em $Não. z_{0}}$ é definido como

${displaystyle f'(z_{0})=lim _{zto z_{0}}{frac {f(z)-f(z_{0})}{z-z_{0}}}}$

Superficialmente, esta definição é formalmente análoga à do derivado de uma função real. No entanto, derivados complexos e funções diferenciadas comportam-se de maneiras significativamente diferentes em comparação com suas contrapartes reais. Em particular, para que este limite exista, o valor do quociente de diferença deve abordar o mesmo número complexo, independentemente da forma como nos aproximamos. $Não. z_{0}}$ no plano complexo. Consequentemente, a diferenciabilidade complexa tem implicações muito mais fortes do que a diferenciação real. Por exemplo, funções holomórficas são infinitamente diferenciadas, enquanto a existência da no derivado não precisa implicar a existência do (n + 1)o derivado para funções reais. Além disso, todas as funções holomórficas satisfazem a condição mais forte de analiticidade, o que significa que a função é, em cada ponto do seu domínio, localmente dada por uma série de energia convergente. Em essência, isso significa que funciona holomorphic em $Não. - Sim.$ pode ser aproximado arbitrariamente bem por polinômios em algum bairro de cada ponto em $Não. - Sim.$. Isto está em contraste agudo com funções reais diferenciadas; existem infinitamente diferentes funções reais que são Nada. analytic; ver Função lisa não-analítica § Uma função lisa que não é nenhum analytic real.

A maioria das funções elementares, incluindo a função exponencial, as funções trigonométricas e todas as funções polinomiais, estendidas apropriadamente a argumentos complexos como funções ${displaystyle mathbb {C} to mathbb Não.$, são holomorfos sobre todo o plano complexo, tornando-os inteiro funções, enquanto funções racionais $- Sim.$, onde p e q são polinômios, são holomorfos em domínios que excluem pontos onde q é zero. Tais funções que são holomórficas em todos os lugares, exceto um conjunto de pontos isolados são conhecidas como funções meromorficas. Por outro lado, as funções ${displaystyle zmapsto Re (z)}$, $|z|}$, e ${displaystyle zmapsto {bar {z}}}$ não são holomórficos em qualquer lugar do plano complexo, como pode ser mostrado por sua incapacidade de satisfazer as condições Cauchy-Riemann (veja abaixo).

Uma propriedade importante de funções holomórficas é a relação entre os derivados parciais de seus componentes reais e imaginários, conhecidos como condições Cauchy-Riemann. Se ${displaystyle f:mathbb] {C} to mathbb Não.$, definido por $(x+iy)=u(x,y)+iv(x,y)}$, Onde? ${displaystyle x,y,u(x,y),v(x,y)in mathbb) Não.$, é holomorfo em uma região $Não. - Sim.$, então para todos ${displaystyle z_{0}in - Sim.$,

${displaystyle {partial f}{partial {bar {z}}}}(z_{0})=0, {text{where }}{frac {partial }{partial {bar {z}}}}mathrel {:=} {frac {1}{2}}left({frac {partial }{partial x}}+i{frac {partial }{partial y}}right). ?$

Em termos das partes reais e imaginárias da função, u e v, isto é equivalente ao par de equações $Não. u_{x}=v_{y}}$ e $Não. u_{y}=-v_{x}}$, onde os subescritos indicam diferenciação parcial. No entanto, as condições Cauchy-Riemann não caracterizam funções holomórficas, sem condições de continuidade adicionais (ver Looman–Menchoff theorem).

Funções holomórficas exibem algumas características notáveis. Por exemplo, o teorema de Picard afirma que o intervalo de uma função inteira pode tomar apenas três formas possíveis: ${displaystyle mathbb {C} } }$, ${displaystyle mathbb (C) {z_{0}}}$, ou $Não. {z_{0}}}$ para alguns ${displaystyle z_{0}in mathbb Não.$. Em outras palavras, se dois números complexos distintos $Não.$ e $Não.$ não estão no intervalo de uma função inteira $Não.$, então $Não.$ é uma função constante. Além disso, uma função holomórfica em um conjunto aberto conectado é determinada pela sua restrição a qualquer subconjunto aberto vazio.

Mapa conforme

Uma grade retangular (top) e sua imagem sob um mapa conformado $Não.$ (bottom). É visto que $Não.$ mapas pares de linhas que se cruzam a 90° para pares de curvas que ainda se cruzam a 90°.

Em matemática, um mapa conformal é uma função que preserva localmente ângulos, mas não necessariamente comprimentos.

Mais formalmente, deixe $Não.$ e $Não.$ ser subconjuntos abertos de ${displaystyle mathbb {R} ^{n}}$. Uma função ${displaystyle f:Uto V}$ é chamado conformal (ou ângulo de preservação) em um ponto ${displaystyle u_{0}in U$ se preserva ângulos entre curvas direcionadas através ${displaystyle u_{0}}$, bem como preservar a orientação. Os mapas conformais preservam ambos os ângulos e as formas de figuras infinitassimalmente pequenas, mas não necessariamente seu tamanho ou curvatura.

A propriedade conformal pode ser descrita em termos da matriz derivada jacobina de uma transformação coordenada. A transformação está em conformidade sempre que o Jacobiano em cada ponto é um escalar positivo vezes uma matriz de rotação (ortogonal com determinante). Alguns autores definem a conformidade para incluir mapeamentos que revertem a orientação, cujos Jacobianos podem ser escritos como qualquer escalar vezes qualquer matriz ortogonal.

Para mapeamentos em duas dimensões, os mapeamentos conformais (preservação de orientação) são precisamente as funções analíticas complexas invertíveis localmente. Em três e maiores dimensões, o teorema de Liouville limita nitidamente os mapeamentos conformados a alguns tipos.

A noção de conformalidade generaliza-se de forma natural para mapas entre os coletores Riemannian ou semi-Riemannian.

Principais resultados

Gráfico de roda de cor da função f(x) = (x² - 1)x - 2 - Eu...)²/x² + 2 + 2Eu....
Hue representa o argumento, brilho a magnitude.

Uma das ferramentas centrais na análise complexa é a integral de linha. A integral de linha em torno de um caminho fechado de uma função que é holomorfa em todos os lugares dentro da área limitada pelo caminho fechado é sempre zero, como afirma o teorema da integral de Cauchy. Os valores de tal função holomórfica dentro de um disco podem ser calculados por uma integral de caminho no limite do disco (como mostrado na fórmula integral de Cauchy). As integrais de caminho no plano complexo são freqüentemente usadas para determinar integrais reais complicadas, e aqui a teoria de resíduos entre outras é aplicável (ver métodos de integração de contorno). Um "pólo" (ou singularidade isolada) de uma função é um ponto onde o valor da função se torna ilimitado, ou "explode". Se uma função tiver tal pólo, então pode-se calcular o resíduo da função ali, que pode ser usado para calcular integrais de caminho envolvendo a função; este é o teorema do poderoso teorema dos resíduos. O notável comportamento de funções holomorfas perto de singularidades essenciais é descrito pelo teorema de Picard. Funções que possuem apenas pólos, mas nenhuma singularidade essencial, são chamadas de meromorfas. As séries de Laurent são equivalentes de valores complexos às séries de Taylor, mas podem ser usadas para estudar o comportamento de funções próximas a singularidades por meio de somas infinitas de funções mais bem compreendidas, como polinômios.

Uma função limitada que é holomorfa em todo o plano complexo deve ser constante; este é o teorema de Liouville. Ele pode ser usado para fornecer uma prova natural e curta para o teorema fundamental da álgebra, que afirma que o corpo de números complexos é algebricamente fechado.

Se uma função é holomórfica em um domínio conectado, seus valores são totalmente determinados por seus valores em qualquer subdomínio menor. Diz-se que a função no domínio maior é continuada analiticamente a partir de seus valores no domínio menor. Isso permite a extensão da definição de funções, como a função zeta de Riemann, que são inicialmente definidas em termos de somas infinitas que convergem apenas em domínios limitados para quase todo o plano complexo. Às vezes, como no caso do logaritmo natural, é impossível continuar analiticamente uma função holomorfa para um domínio não simplesmente conectado no plano complexo, mas é possível estendê-la para uma função holomorfa em uma superfície intimamente relacionada conhecida como Superfície de Riemann.

Tudo isso se refere à análise complexa em uma variável. Há também uma teoria muito rica de análise complexa em mais de uma dimensão complexa na qual as propriedades analíticas, como a expansão da série de potências, são transportadas, enquanto a maioria das propriedades geométricas das funções holomorfas em uma dimensão complexa (como a conformidade) não são transferidas.. O teorema de mapeamento de Riemann sobre a relação conforme de certos domínios no plano complexo, que pode ser o resultado mais importante na teoria unidimensional, falha drasticamente em dimensões superiores.

Uma das principais aplicações de certos espaços complexos é na mecânica quântica como funções de onda.