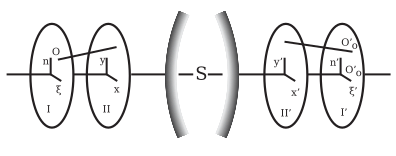Aberração óptica
Em óptica, aberração é uma propriedade de sistemas ópticos, como lentes, que faz com que a luz se espalhe por alguma região do espaço em vez de focalizada em um ponto. As aberrações fazem com que a imagem formada por uma lente fique borrada ou distorcida, com a natureza da distorção dependendo do tipo de aberração. A aberração pode ser definida como um afastamento do desempenho de um sistema óptico das previsões da óptica paraxial. Em um sistema de imagem, ocorre quando a luz de um ponto de um objeto não converge para (ou não diverge de) um único ponto após a transmissão pelo sistema. As aberrações ocorrem porque a teoria paraxial simples não é um modelo completamente preciso do efeito de um sistema óptico na luz, e não devido a falhas nos elementos ópticos.
Um sistema óptico de formação de imagem com aberração produzirá uma imagem que não é nítida. Os fabricantes de instrumentos ópticos precisam corrigir os sistemas ópticos para compensar a aberração.
A aberração pode ser analisada com as técnicas de óptica geométrica. Os artigos sobre reflexão, refração e cáustica discutem as características gerais dos raios refletidos e refratados.
Visão geral
Com uma lente ideal, a luz de qualquer ponto em um objeto passaria pela lente e se reuniria em um único ponto no plano da imagem (ou, de forma mais geral, a imagem superfície). As lentes reais não focalizam a luz exatamente em um único ponto, no entanto, mesmo quando são feitas com perfeição. Esses desvios do desempenho idealizado da lente são chamados de aberrações da lente.
As aberrações se dividem em duas classes: monocromáticas e cromáticas. As aberrações monocromáticas são causadas pela geometria da lente ou espelho e ocorrem tanto quando a luz é refletida quanto quando é refratada. Eles aparecem mesmo quando se usa luz monocromática, daí o nome.
As aberrações cromáticas são causadas pela dispersão, a variação do índice de refração de uma lente com o comprimento de onda. Por causa da dispersão, diferentes comprimentos de onda de luz se concentram em pontos diferentes. A aberração cromática não aparece quando a luz monocromática é usada.
Aberrações monocromáticas
As aberrações monocromáticas mais comuns são:
- Defocus
- Abertura esférica
- Coma
- Astigmatismo
- curvatura de campo
- distorção de imagem
Embora a desfocagem seja tecnicamente a ordem mais baixa das aberrações ópticas, geralmente não é considerada uma aberração da lente, pois pode ser corrigida movendo a lente (ou o plano da imagem) para trazer o plano da imagem para o foco óptico da lente.
Além dessas aberrações, o pistão e a inclinação são efeitos que alteram a posição do ponto focal. Pistão e inclinação não são verdadeiras aberrações ópticas, pois quando uma frente de onda perfeita é alterada por pistão e inclinação, ela ainda formará uma imagem perfeita e livre de aberrações, apenas deslocada para uma posição diferente.
Aberrações cromáticas
A aberração cromática ocorre quando diferentes comprimentos de onda não são focados no mesmo ponto. Os tipos de aberração cromática são:
- Aberração cromática axial (ou "longitudinal")
- Aberração cromática posterior (ou "transversa")
Teoria da aberração monocromática
Em um sistema óptico perfeito na teoria clássica da óptica, os raios de luz provenientes de qualquer ponto do objeto se unem em um ponto da imagem; e, portanto, o espaço do objeto é reproduzido em um espaço da imagem. A introdução de termos auxiliares simples, devido a Gauss, denominados distâncias focais e planos focais, permite a determinação do imagem de qualquer objeto para qualquer sistema. A teoria gaussiana, porém, só é verdadeira enquanto os ângulos formados por todos os raios com o eixo óptico (o eixo simétrico do sistema) forem infinitamente pequenos, ou seja, com objetos, imagens e lentes infinitesimais; na prática essas condições podem não se concretizar, e as imagens projetadas por sistemas não corrigidos são, em geral, mal definidas e muitas vezes borradas se a abertura ou o campo de visão ultrapassar certos limites.
As investigações de James Clerk Maxwell e Ernst Abbe mostraram que as propriedades dessas reproduções, ou seja, a posição relativa e a magnitude das imagens, não são propriedades especiais de sistemas ópticos, mas consequências necessárias da suposição (segundo Abbe) de a reprodução de todos os pontos de um espaço em pontos de imagem, e são independentes da maneira como a reprodução é efetuada. Esses autores mostraram, no entanto, que nenhum sistema óptico pode justificar essas suposições, pois são contrárias às leis fundamentais de reflexão e refração. Conseqüentemente, a teoria gaussiana fornece apenas um método conveniente de aproximação da realidade; sistemas ópticos realistas ficam aquém desse ideal inatingível. Atualmente, tudo o que pode ser realizado é a projeção de um único plano sobre outro plano; mas mesmo nisso, sempre ocorrem aberrações e pode ser improvável que elas sejam totalmente corrigidas.
Aberração de pontos axiais (aberração esférica no sentido restrito)
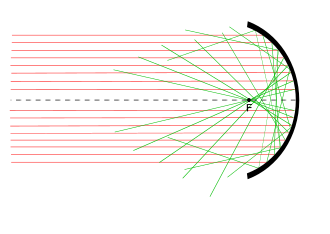
Seja S (fig. 1) qualquer sistema óptico, os raios provenientes de um ponto do eixo O sob um ângulo u1 se unirão no ponto do eixo O'1; e aqueles sob um ângulo u2 no eixo ponto O'2. Se houver refração em uma superfície esférica coletiva ou através de uma lente positiva fina, O'2 ficará na frente de O'1 desde que o ângulo u2 seja maior que u1 (sob correção); e, inversamente, com uma superfície ou lentes dispersivas (sobrecorreção). A cáustica, no primeiro caso, assemelha-se ao sinal > (Maior que); na segunda < (menor que). Se o ângulo u1 for muito pequeno, O'1 é a imagem gaussiana; e O'1 O'2 é denominado aberração longitudinal, e O'1R a aberração lateral dos lápis com abertura u2. Se o lápis com o ângulo u2 é o da aberração máxima de todos os lápis transmitidos, então em um plano perpendicular ao eixo em O'1 existe um disco de confusão circular de raio O& #39;1R, e em um plano paralelo em O'2 outro de raio O'2R2; entre esses dois está situado o disco de menor confusão.
A maior abertura dos lápis, que participam da reprodução de O, ou seja, o ângulo u, é geralmente determinada pela margem de uma das lentes ou por um furo em uma placa fina colocada entre, antes ou atrás das lentes do sistema. Este orifício é denominado stop ou diafragma; Abbe usou o termo parada de abertura tanto para o orifício quanto para a margem limitante da lente. A componente S1 do sistema, situada entre o batente da abertura e o objeto O, projeta uma imagem do diafragma, denominada por Abbe de pupila de entrada; a pupila de saída é a imagem formada pelo componente S2, que é colocado atrás do batente de abertura. Todos os raios que saem de O e passam pelo batente de abertura também passam pelas pupilas de entrada e saída, pois são imagens do batente de abertura. Como a abertura máxima dos lápis saindo de O é o ângulo u subtendido pela pupila de entrada neste ponto, a magnitude da aberração será determinada pela posição e diâmetro da pupila de entrada. Se o sistema estiver totalmente atrás do batente de abertura, então este é o próprio aluno de entrada ( batente frontal); se totalmente na frente, é a pupila de saída (back stop).
Se o ponto do objeto estiver infinitamente distante, todos os raios recebidos pelo primeiro membro do sistema são paralelos, e suas interseções, após atravessarem o sistema, variam de acordo com sua altura de incidência perpendicular, ou seja, sua distância do eixo. Essa distância substitui o ângulo u nas considerações anteriores; e a abertura, ou seja, o raio da pupila de entrada, é o seu valor máximo.
Aberração de elementos, ou seja, objetos menores em ângulos retos com o eixo
Se os raios que saem de O (fig. 1) são concorrentes, não se segue que pontos em uma parte de um plano perpendicular em O ao eixo também sejam concorrentes, mesmo que a parte do plano seja muito pequena. À medida que o diâmetro da lente aumenta (ou seja, com o aumento da abertura), o ponto vizinho N será reproduzido, mas acompanhado por aberrações comparáveis em magnitude a ON. Essas aberrações são evitadas se, de acordo com Abbe, a condição do seno, sin u'1/sin u1=sin u'2/sin u2, vale para todos os raios que reproduzem o ponto O. Se o ponto objeto O estiver infinitamente distante, u1 e u2 devem ser substituídos por h1 e h2, as alturas perpendiculares de incidência; a condição de seno então se torna sen u'1/h1=sin u'2/h2. Um sistema que cumpre esta condição e livre de aberração esférica é chamado aplanático (do grego a-, privativo, plann, um errante). Esta palavra foi usada pela primeira vez por Robert Blair para caracterizar um acromatismo superior e, posteriormente, por muitos escritores para denotar a liberdade de aberração esférica também.
Como a aberração aumenta com a distância do raio do centro da lente, a aberração aumenta à medida que o diâmetro da lente aumenta (ou, correspondentemente, com o diâmetro da abertura) e, portanto, pode ser minimizada reduzindo a abertura, ao custo de reduzir também a quantidade de luz que atinge o plano da imagem.
Aberração de pontos de objetos laterais (pontos além do eixo) com lápis estreitos — astigmatismo
Um ponto O (fig. 2) a uma distância finita do eixo (ou com um objeto infinitamente distante, um ponto que subtende um ângulo finito no sistema) é, em geral, mesmo assim não nitidamente reproduzido se o lápis dos raios que saem dele e atravessam o sistema é feito infinitamente estreito reduzindo o limite de abertura; tal lápis consiste nos raios que podem passar do ponto do objeto através da agora infinitamente pequena pupila de entrada. É visto (ignorando casos excepcionais) que o lápis não atinge a superfície refratora ou refletora em ângulos retos; portanto é astigmático (Gr. a-, privativo, stigmia, um ponto). Chamando o raio central que passa pela pupila de entrada de eixo do lápis ou raio principal, pode-se dizer: os raios do lápis se interceptam, não em um ponto, mas em duas linhas focais, que podem ser consideradas perpendiculares ao raio principal; destes, um encontra-se no plano que contém o raio principal e o eixo do sistema, ou seja, na primeira seção principal ou seção meridional, e o outro em ângulo reto com isto é, na segunda seção principal ou seção sagital. Recebemos, portanto, em nenhum plano interceptador atrás do sistema, como, por exemplo, uma tela de focalização, uma imagem do ponto objeto; por outro lado, em cada um dos dois planos, as linhas O' e O" são formados separadamente (em planos vizinhos as elipses são formadas), e em um plano entre O' e O" um círculo de menor confusão. O intervalo O'O", denominado diferença astigmática, aumenta, em geral, com o ângulo W feito pelo raio principal OP com o eixo do sistema, ou seja, com o campo de visão. Duas superfícies de imagens astigmáticas correspondem a um plano de objeto; e estes estão em contato no ponto do eixo; de um lado estão as linhas focais do primeiro tipo, do outro, as do segundo. Os sistemas nos quais as duas superfícies astigmáticas coincidem são denominados anastigmáticos ou estigmáticos.
Sir Isaac Newton foi provavelmente o descobridor da astigmação; a posição das linhas astigmáticas da imagem foi determinada por Thomas Young; e a teoria foi desenvolvida por Allvar Gullstrand. Uma bibliografia de P. Culmann é fornecida em Die Bilderzeugung in optischen Instrumenten de Moritz von Rohr.
Aberração de pontos de objetos laterais com lápis largos — coma
Ao abrir mais o batente, surgem desvios semelhantes para os pontos laterais, como já foi discutido para os pontos axiais; mas neste caso eles são muito mais complicados. O curso dos raios na seção meridional não é mais simétrico ao raio principal do lápis; e em um plano de interceptação aparece, em vez de um ponto luminoso, um remendo de luz, não simétrico em relação a um ponto, e freqüentemente exibindo uma semelhança com um cometa tendo sua cauda direcionada para ou longe do eixo. A partir desta aparência leva o seu nome. A forma assimétrica do lápis meridional - anteriormente a única considerada - é coma apenas no sentido mais restrito; outros erros de coma foram tratados por Arthur König e Moritz von Rohr, e mais tarde por Allvar Gullstrand.
Curvatura do campo da imagem
Se os erros acima forem eliminados, as duas superfícies astigmáticas unidas e uma imagem nítida obtida com uma grande abertura - resta a necessidade de corrigir a curvatura da superfície da imagem, especialmente quando a imagem deve ser recebida em um plano superfície, por ex. na fotografia. Na maioria dos casos, a superfície é côncava em direção ao sistema.
Distorção da imagem
Mesmo que a imagem seja nítida, ela pode ficar distorcida em comparação com a projeção pinhole ideal. Na projeção pinhole, a ampliação de um objeto é inversamente proporcional à sua distância da câmera ao longo do eixo óptico, de modo que uma câmera apontada diretamente para uma superfície plana reproduz essa superfície plana. A distorção pode ser considerada como o alongamento não uniforme da imagem ou, de forma equivalente, como uma variação na ampliação ao longo do campo. Enquanto "distorção" pode incluir deformação arbitrária de uma imagem, os modos mais pronunciados de distorção produzidos pela ótica de imagem convencional é a "distorção de barril", na qual o centro da imagem é ampliado mais do que o perímetro (figura 3a). O inverso, em que o perímetro é ampliado mais do que o centro, é conhecido como "distorção de alfinetes" (figura 3b). Esse efeito é chamado de distorção de lente ou distorção de imagem e existem algoritmos para corrigi-lo.
Sistemas livres de distorção são chamados ortoscópicos (orthos, direito, skopein para olhar) ou retilíneos (linhas retas).
Esta aberração é bastante distinta daquela da nitidez da reprodução; na reprodução não nítida, surge a questão da distorção se apenas partes do objeto puderem ser reconhecidas na figura. Se, em uma imagem não nítida, uma mancha de luz corresponder a um ponto do objeto, o centro de gravidade da mancha pode ser considerado como o ponto da imagem, sendo este o ponto onde o plano receptor da imagem, por exemplo, uma tela de focagem, intercepta o raio que passa pelo meio da parada. Essa suposição é justificada se uma imagem ruim na tela de focagem permanecer estacionária quando a abertura for diminuída; na prática, isso geralmente ocorre. Este raio, chamado por Abbe de raio principal (não confundir com os raios principais da teoria gaussiana), passa pelo centro da pupila de entrada antes da primeira refração, e o centro da pupila de saída após a última refração. Disto se segue que a exatidão do desenho depende unicamente dos raios principais; e é independente da nitidez ou curvatura do campo da imagem. Referindo-se à fig. 4, temos O'Q'/OQ = a' tan w'/a tan w = 1/N, onde N é a escala ou ampliação da imagem. Para que N seja constante para todos os valores de w, a' tan w'/a tan w também deve ser constante. Se a razão a'/a for suficientemente constante, como costuma ser o caso, a relação acima se reduz à condição de Airy, ou seja, tan w'/ tan w= uma constante. Esta relação simples (ver Camb. Phil. Trans., 1830, 3, p. 1) é cumprida em todos os sistemas que são simétricos em relação ao seu diafragma (abreviadamente denominados objetivos simétricos ou holossimétricos), ou que consistem em dois componentes iguais, mas de tamanhos diferentes, colocados a partir do diafragma na proporção de seu tamanho e apresentando a mesma curvatura a ele (objetivas hemissimétricas); nesses sistemas tan w' / t w = 1.
A constância de a'/a necessária para que essa relação se mantenha foi apontada por R. H. Bow (Brit. Journ. Photog., 1861) e Thomas Sutton (Photographic Notes, 1862); foi tratado por O. Lummer e por M. von Rohr (Zeit. f. Instrumentenk., 1897, 17 e 1898, 18, p. 4). Requer que o meio do batente da abertura seja reproduzido nos centros das pupilas de entrada e saída sem aberração esférica. M. von Rohr mostrou que, para sistemas que não cumprem nem a condição de Airy nem a de Bow-Sutton, a razão a' cos w'/a tan w será constante para uma distância do objeto. Esta condição combinada é exatamente cumprida por objetivas holossimétricas reproduzindo com a escala 1, e por hemissimétricas, se a escala de reprodução for igual à razão dos tamanhos dos dois componentes.
Modelo de aberrações de Zernike
Perfis de frentes de onda circulares associados a aberrações podem ser modelados matematicamente usando polinômios de Zernike. Desenvolvido por Frits Zernike na década de 1930, os polinômios de Zernike são ortogonais sobre um círculo de raio unitário. Um perfil de frente de onda complexo e aberrado pode ser ajustado à curva com polinômios de Zernike para produzir um conjunto de coeficientes de ajuste que representam individualmente diferentes tipos de aberrações. Esses coeficientes de Zernike são linearmente independentes, portanto, contribuições de aberrações individuais para uma frente de onda geral podem ser isoladas e quantificadas separadamente.
Existem polinômios de Zernike pares e ímpares. Os polinômios pares de Zernike são definidos como
- Z.nm(? ? ,φ φ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rnm(? ? )e (mφ φ )Não. Z_{n}^{m}(rhophi)=R_{n}^{m}(rho),cos(m,phi)!}
e os polinômios ímpares de Zernike como
- Z.n- Sim. - Sim. m(? ? ,φ φ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Rnm(? ? )pecado (mφ φ ),Não. Z_{n}^{-m}(rhophi)=R_{n}^{m}(rho),sin(m,phi),!}
Onde? m e n são inteiros nonnegative com n≥ ≥ m- Sim., Φ é o ângulo azimutal em radianos, e ρ é a distância radial normalizada. Os polinômios radiais RnmNão. R_{n}^{m}} não têm dependência azimutal, e são definidos como
- Rnm(? ? )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0(n- Sim. - Sim. m)/2(- Sim. - Sim. 1)k(n- Sim. - Sim. k)!k!((n+m)/2- Sim. - Sim. k)!((n- Sim. - Sim. m)/2- Sim. - Sim. k)!? ? n- Sim. - Sim. 2ksen- Sim. - Sim. mmesmoNão. R_{n}^{m}(rho)=!sum _{k=0}^{(n-m)/2}!!!{frac {(-1)^{k},(n-k)!}{k!,(n+m)/2-k)!,(n-m)/2-k)!}};rho ^{n-2,k}quad Sim.
e Rnm(? ? )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0Não. R_{n}^{m}(rho)=0} se n- Sim. - Sim. mNão. Não. É estranho.
Os primeiros polinômios de Zernike, multiplicados por seus respectivos coeficientes de ajuste, são:
| um0× × 1Não. a_{0}times 1 | "Piston", igual ao valor médio da frente das ondas |
| um1× × ? ? e (φ φ ){displaystyle a_{1}times rho cos(phi)} | "X-Tilt", o desvio do feixe geral na direção sagital |
| um2× × ? ? pecado (φ φ ){displaystyle a_{2}times rho sin(phi)} | "Y-Tilt", o desvio do feixe geral na direção tangencial |
| um3× × (2? ? 2- Sim. - Sim. 1){displaystyle a_{3}times (2rho ^{2}-1)} | "Defoco", uma onda parabólica que resulta de estar fora de foco |
| um4× × ? ? 2e (2φ φ ){displaystyle a_{4}times rho ^{2}cos(2phi)} | "0° Astigmatismo", uma forma cilíndrica ao longo do eixo X ou Y |
| um5× × ? ? 2pecado (2φ φ ){displaystyle a_{5}times rho ^{2}sin(2phi)} | "45° Astigmatismo", uma forma cilíndrica orientada a ±45° do eixo X |
| um6× × (3? ? 2- Sim. - Sim. 2)? ? e (φ φ ){displaystyle a_{6}times (3rho ^{2}-2)rho cos(phi)} | "X-Coma", imagem comática que pisca na direção horizontal |
| um7× × (3? ? 2- Sim. - Sim. 2)? ? pecado (φ φ ){displaystyle a_{7}times (3rho ^{2}-2)rho sin(phi)} | "Y-Coma", imagem comática que pisca na direção vertical |
| um8× × (6? ? 4- Sim. - Sim. 6? ? 2+1){displaystyle a_{8}times (6rho ^{4}-6rho ^{2}+1)} | "Sua ordem aberração esférica" |
Onde? ? ? - Sim. é o raio de aluno normalizado com 0≤ ≤ ? ? ≤ ≤ 1{displaystyle 0leq rho leq 1, φ φ - Sim. é o ângulo azimutal em torno do aluno com 0≤ ≤ φ φ ≤ ≤ 2D D {displaystyle 0leq phi leq 2pi ?, e os coeficientes de fixação um0,...... ,um8{displaystyle a_{0},ldotsa_{8}} são os erros de onda em comprimentos de onda.
Como na síntese de Fourier usando senos e cossenos, uma frente de onda pode ser perfeitamente representada por um número suficientemente grande de polinômios de Zernike de ordem superior. No entanto, frentes de onda com gradientes muito acentuados ou estrutura de frequência espacial muito alta, como as produzidas pela propagação através de turbulência atmosférica ou campos de fluxo aerodinâmico, não são bem modeladas pelos polinômios de Zernike, que tendem a filtrar a definição espacial fina na frente de onda. Nesse caso, outros métodos de ajuste, como fractais ou decomposição de valor singular, podem produzir melhores resultados de ajuste.
Os polinômios do círculo foram introduzidos por Frits Zernike para avaliar a imagem pontual de um sistema óptico aberrado levando em conta os efeitos da difração. A imagem pontual perfeita na presença de difração já havia sido descrita por Airy, já em 1835. Demorou quase cem anos para chegar a uma teoria abrangente e modelagem da imagem pontual de sistemas aberrados (Zernike e Nijboer). A análise de Nijboer e Zernike descreve a distribuição de intensidade próxima ao plano focal ótimo. Uma teoria estendida que permite o cálculo da amplitude e intensidade da imagem pontual sobre um volume muito maior na região focal foi desenvolvida recentemente (teoria estendida de Nijboer-Zernike). Essa teoria estendida de Nijboer-Zernike de formação de imagem pontual ou "função de propagação de ponto" encontrou aplicações em pesquisas gerais sobre formação de imagem, especialmente para sistemas com alta abertura numérica e na caracterização de sistemas ópticos com relação a suas aberrações.
Tratamento analítico de aberrações
A revisão anterior dos vários erros de reprodução pertence à teoria Abbe das aberrações, na qual as aberrações definidas são discutidas separadamente; adapta-se bem às necessidades práticas, pois na construção de um instrumento óptico procura-se eliminar certos erros, cuja seleção é justificada pela experiência. No sentido matemático, porém, essa seleção é arbitrária; a reprodução de um objeto finito com uma abertura finita acarreta, com toda probabilidade, um número infinito de aberrações. Este número é apenas finito se o objeto e a abertura forem considerados infinitamente pequenos de uma certa ordem; e a cada ordem de pequenez infinita, isto é, a cada grau de aproximação à realidade (a objectos finitos e aberturas), está associado um certo número de aberrações. Essa conexão só é fornecida por teorias que tratam as aberrações de forma geral e analítica por meio de séries indefinidas.
Um raio proveniente de um ponto objeto O (fig. 5) pode ser definido pelas coordenadas (ξ, η). Deste ponto O em um objeto plano I, perpendicularmente ao eixo, e duas outras coordenadas (x, y), o ponto em que o raio intercepta a pupila de entrada, ou seja, o plano II. Da mesma forma, o raio imagem correspondente pode ser definido pelos pontos (ξ', η') e (x', y'), nos planos I' e II'. As origens desses quatro sistemas de coordenadas planas podem ser colineares com o eixo do sistema óptico; e os eixos correspondentes podem ser paralelos. Cada uma das quatro coordenadas ξ', η', x', y' são funções de ξ, η, x, y; e se for assumido que o campo de visão e a abertura são infinitamente pequenos, então ξ, η, x, y são da mesma ordem de infinitesimais; consequentemente, expandindo ξ', η', x', y' em potências ascendentes de ξ, η, x, y, obtêm-se séries nas quais só é necessário considerar as potências mais baixas. É facilmente visto que, se o sistema óptico for simétrico, as origens dos sistemas de coordenadas colineares com o eixo óptico e os eixos correspondentes paralelos, então, alterando os sinais de ξ, η, x, y, os valores ξ', η', x', y' devem igualmente mudar de sinal, mas manter seus valores aritméticos; isso significa que as séries são restritas a potências ímpares das variáveis não marcadas.
A natureza da reprodução consiste nos raios procedentes de um ponto O sendo unidos em outro ponto O'; em geral, este não será o caso, para ξ', η' variam se ξ, η são constantes, mas x, y variável. Pode-se supor que os planos I' e II' são desenhados onde as imagens dos planos I e II são formadas por raios próximos ao eixo pelas regras gaussianas ordinárias; e por uma extensão destas regras, mas não correspondendo à realidade, o ponto imagem de Gauss O'0, com as coordenadas ξ'0, η&# 39;0, do ponto O a alguma distância do eixo. Escrevendo Dξ'=ξ'-ξ'0 e Dη'=η'-η'0, depois Dξ&# 39; e Dη' são as aberrações pertencentes a ξ, η e x, y, e são funções dessas grandezas que, quando expandidas em série, contêm apenas potências ímpares, pelos mesmos motivos dados acima. Devido às aberrações de todos os raios que passam por O, uma mancha de luz, dependendo em tamanho das potências mais baixas de ξ, η, x, y que as aberrações contêm, será formada no plano I'. Esses graus, denominados por J. Petzval as ordens numéricas da imagem, são, portanto, apenas potências ímpares; a condição para a formação de uma imagem da ordem m é que na série para Dξ' e Dη' os coeficientes das potências do 3º, 5º...(m-2)º graus devem desaparecer. Sendo as imagens da teoria de Gauss de terceira ordem, o próximo problema é obter uma imagem de 5ª ordem, ou seja, fazer com que os coeficientes das potências de 3º grau sejam zero. Isso requer a satisfação de cinco equações; ou seja, há cinco alterações de 3ª ordem, cujo desaparecimento produz uma imagem de 5ª ordem.
A expressão desses coeficientes em termos das constantes do sistema óptico, ou seja, os raios, espessuras, índices de refração e distâncias entre as lentes, foi resolvida por L. Seidel; em 1840, J. Petzval construiu sua objetiva de retrato, a partir de cálculos semelhantes que nunca foram publicados. A teoria foi elaborada por S. Finterswalder, que também publicou um artigo póstumo de Seidel contendo uma breve visão de seu trabalho; uma forma mais simples foi dada por A. Kerber. A. Konig e M. von Rohr representaram o método de Kerber e deduziram as fórmulas de Seidel a partir de considerações geométricas baseadas no método de Abbe e interpretaram os resultados analíticos geometricamente.
As aberrações também podem ser expressas por meio da função característica do sistema e seus coeficientes diferenciais, em vez dos raios, &c., das lentes; essas fórmulas não são imediatamente aplicáveis, mas fornecem, no entanto, a relação entre o número de aberrações e a ordem. Sir William Rowan Hamilton (Relatório da Associação Britânica, 1833, p. 360) derivou assim as aberrações de terceira ordem; e em tempos posteriores o método foi seguido por Clerk Maxwell (Proc. London Math. Soc., 1874–1875; (veja também os tratados de R. S. Heath e L. A. Herman), M. Thiesen (Berlin. Akad. Sitzber., 1890, 35, p. 804), H. Bruns (Leipzig. Math. Phys. Ber., 1895, 21, p. 410), e particularmente com sucesso por K. Schwarzschild (Göttingen. Akad. Abhandl., 1905, 4, No. 1), que assim descobriu as aberrações da 5ª ordem (das quais existem nove), e possivelmente a prova mais curta das fórmulas práticas (Seidel). A. Gullstrand (vide supra, e Ann. d. Phys., 1905, 18, p. 941) fundou sua teoria das aberrações na geometria diferencial de superfícies.
As aberrações de terceira ordem são: (1) aberração do ponto do eixo; (2) aberração de pontos cuja distância do eixo é muito pequena, menor que de terceira ordem — o desvio da condição senoidal e a coma aqui caem juntos em uma classe; (3) astigmatismo; (4) curvatura do campo; (5) distorção.
- Aberração da terceira ordem de pontos de eixo é tratada em todos os livros-texto sobre óptica. É muito importante no design do telescópio. Na abertura dos telescópios é geralmente tomado como o diâmetro linear do objetivo. Não é o mesmo que a abertura do microscópio que se baseia no aluno de entrada ou campo de visão como visto do objeto e é expresso como uma medição angular. Aberrações de ordem mais elevada no projeto do telescópio podem ser negligenciadas principalmente. Para microscópios não pode ser negligenciado. Para uma única lente de espessura muito pequena e dada potência, a aberração depende da relação do radii r:r', e é um mínimo (mas nunca zero) para um determinado valor desta relação; varia inversamente com o índice de refração (o poder da lente restante constante). A aberração total de duas ou mais lentes muito finas em contato, sendo a soma das aberrações individuais, pode ser zero. Isso também é possível se as lentes tiverem o mesmo sinal algébrico. De lentes positivas finas com n=1.5, quatro são necessários para corrigir a aberração esférica da terceira ordem. Estes sistemas, no entanto, não são de grande importância prática. Na maioria dos casos, duas lentes finas são combinadas, uma das quais tem apenas tão forte uma aberração positiva (subcorreção, vide supra) como o outro negativo; o primeiro deve ser uma lente positiva e o segundo uma lente negativa; os poderes, entretanto: podem diferir, de modo que o efeito desejado da lente seja mantido. É geralmente uma vantagem para garantir um grande efeito refrativo por vários mais fracos do que por uma lente de alta potência. Por um, e também por vários, e mesmo por um número infinito de lentes finas em contato, não mais do que dois pontos de eixo podem ser reproduzidos sem aberração da terceira ordem. A liberdade de aberração para dois pontos de eixo, um dos quais é infinitamente distante, é conhecido como A condição da Herschel. Todas estas regras são válidas, já que as espessuras e distâncias das lentes não devem ser consideradas.
- A condição de liberdade de coma na terceira ordem também é de importância para os objetivos do telescópio; é conhecida como A condição de Fraunhofer. (4) Depois de eliminar a aberração No eixo, coma e astigmatismo, a relação para o achado do campo na terceira ordem é expressa pelo Equação de Petzval, S1/r(n'−n) = 0, onde r é o raio de uma superfície refratante, n e n' os índices de refração dos meios vizinhos, e S o sinal de soma para todas as superfícies refratantes.
Eliminação prática de aberrações
O problema clássico de imagem é reproduzir perfeitamente um plano finito (o objeto) em outro plano (a imagem) através de uma abertura finita. É impossível fazer isso perfeitamente para mais de um tal par de planos (isso foi comprovado com generalidade crescente por Maxwell em 1858, por Bruns em 1895 e por Carathéodory em 1926, ver resumo em Walther, A., J. Opt. Soc. Am. A 6, 415–422 (1989)). Para um único par de planos (por exemplo, para um único ajuste de foco de uma objetiva), no entanto, o problema pode, em princípio, ser resolvido perfeitamente. Exemplos de tal sistema teoricamente perfeito incluem a lente Luneburg e o olho de peixe Maxwell.
Métodos práticos resolvem este problema com uma precisão que na maioria das vezes é suficiente para a finalidade específica de cada espécie de instrumento. O problema de encontrar um sistema que reproduza um dado objeto em um dado plano com dada ampliação (na medida em que as aberrações devem ser levadas em conta) poderia ser resolvido por meio da teoria da aproximação; na maioria dos casos, no entanto, as dificuldades analíticas eram muito grandes para métodos de cálculo mais antigos, mas podem ser amenizadas pela aplicação de sistemas de computador modernos. Soluções, no entanto, foram obtidas em casos especiais. Atualmente, os construtores quase sempre empregam o método inverso: eles compõem um sistema a partir de certas experiências, muitas vezes bastante pessoais, e testam, pelo cálculo trigonométrico das trajetórias de vários raios, se o sistema dá a reprodução desejada (exemplos são dados em A. Gleichen, Lehrbuch der geometrischen Optik, Leipzig e Berlim, 1902). Os raios, espessuras e distâncias são continuamente alterados até que os erros da imagem se tornem suficientemente pequenos. Por este método, apenas certos erros de reprodução são investigados, especialmente membros individuais, ou todos, daqueles mencionados acima. A teoria da aproximação analítica é muitas vezes empregada provisoriamente, uma vez que sua precisão geralmente não é suficiente.
Para tornar a aberração esférica e o desvio da condição senoidal pequenos em toda a abertura, é dado um raio com um ângulo finito de abertura u* (largura objetos infinitamente distantes: com uma altura finita de incidência h*) a mesma distância de interseção, e a mesma razão senoidal para um vizinho do eixo (u* ou h* não pode ser muito menor que a maior abertura U ou H a ser usada no sistema). Os raios com ângulo de abertura menor que u* não teriam a mesma distância de interseção e a mesma razão senoidal; esses desvios são chamados de zonas e o construtor se esforça para reduzi-los ao mínimo. O mesmo vale para os erros que dependem do ângulo do campo de visão, w: astigmatismo, curvatura do campo e distorção são eliminados para um valor definido, w*, zonas de astigmatismo, curvatura do campo e distorção, atender a valores menores de w. Os oculistas práticos nomeiam tais sistemas: corrigidos para o ângulo de abertura u* (a altura de incidência h*) ou o ângulo de campo de visão w*. A aberração esférica e as mudanças das relações senoidais são representados graficamente como funções da abertura, da mesma forma que os desvios de duas superfícies astigmáticas da imagem do plano da imagem do ponto do eixo são representados como funções dos ângulos do campo de visão.
A forma final de um sistema prático, portanto, repousa no compromisso; o aumento da abertura resulta em uma diminuição do campo de visão disponível e vice-versa. Mas a abertura maior dará a resolução maior. O seguinte pode ser considerado típico:
- A abertura maior; as correções necessárias são — para o ponto do eixo, e condição do pecado; erros do campo de visão são quase desconsiderados; exemplo — objetivos do microscópio de alta potência.
- Lente angular ampla; correções necessárias são — para o astigmatismo, curvatura de campo e distorção; erros da abertura apenas ligeiramente considerados; exemplos — objetivos angulares mais largos fotográficos e oculares. Entre esses exemplos extremos está a lente normal: isso é corrigido mais no que diz respeito à abertura; objetivos para grupos mais no que diz respeito ao campo de visão.
- Lentes de foco longo têm pequenos campos de visão e aberrações no eixo são muito importantes. Por isso, as zonas serão mantidas o menor possível e o design deve enfatizar a simplicidade. Devido a essas lentes são os melhores para computação analítica.
Aberração cromática ou de cor
Em sistemas ópticos compostos por lentes, a posição, magnitude e erros da imagem dependem dos índices de refração do vidro empregado (ver Lente (ótica) e Aberração monocromática, acima). Como o índice de refração varia com a cor ou comprimento de onda da luz (ver dispersão), segue-se que um sistema de lentes (não corrigidas) projeta imagens de cores diferentes em lugares e tamanhos um tanto diferentes e com aberrações diferentes; ou seja, existem diferenças cromáticas das distâncias de interseção, de ampliações e de aberrações monocromáticas. Se for empregada luz mista (por exemplo, luz branca) todas essas imagens são formadas e causam uma confusão, denominada aberração cromática; por exemplo, em vez de uma margem branca sobre um fundo escuro, percebe-se uma margem colorida, ou espectro estreito. A ausência desse erro é chamada de acromatismo, e um sistema óptico assim corrigido é chamado de acromático. Diz-se que um sistema está subcorrigido cromaticamente quando apresenta o mesmo tipo de erro cromático que uma lente positiva delgada, caso contrário, diz-se que está supercorrigido.
Se, em primeiro lugar, as aberrações monocromáticas forem negligenciadas - em outras palavras, a teoria gaussiana for aceita - então toda reprodução é determinada pelas posições dos planos focais e pela magnitude das distâncias focais, ou se as distâncias focais os comprimentos, como ordinariamente acontece, são iguais, por três constantes de reprodução. Estas constantes são determinadas pelos dados do sistema (raios, espessuras, distâncias, índices, etc., das lentes); portanto, sua dependência do índice de refração e, conseqüentemente, da cor, é calculável. Os índices de refração para diferentes comprimentos de onda devem ser conhecidos para cada tipo de vidro utilizado. Desta forma, são mantidas as condições de que qualquer constante de reprodução é igual para duas cores diferentes, isto é, esta constante é acromatizada. Por exemplo, é possível, com uma lente espessa no ar, acromatizar a posição de um plano focal da magnitude da distância focal. Se todas as três constantes de reprodução forem acromatizadas, então a imagem Gaussiana para todas as distâncias dos objetos é a mesma para as duas cores, e o sistema é dito estar em acromatismo estável.
Na prática é mais vantajoso (após Abbe) determinar a aberração cromática (por exemplo, a da distância de interseção) para uma posição fixa do objeto, e expressá-la por uma soma na qual cada componente limita a quantidade devido a cada superfície refratora. Em um plano contendo o ponto de imagem de uma cor, outra cor produz um disco de confusão; isso é semelhante à confusão causada por duas zonas na aberração esférica. Para objetos infinitamente distantes, o raio do disco cromático de confusão é proporcional à abertura linear e independente da distância focal (vide supra, Aberração monocromática do ponto do eixo); e como esse disco se torna menos nocivo com o aumento da imagem de um determinado objeto, ou com o aumento da distância focal, segue-se que a deterioração da imagem é proporcional à razão entre a abertura e a distância focal, ou seja, o relativo abertura. (Isso explica as gigantescas distâncias focais em voga antes da descoberta do acromatismo.)
Exemplos:
- In a very thin lens, in air, only one constant of reproduction is to be observed, since the focal length and the distance of the focal point are equal. If the refractive index for one color be
n
{displaystyle n}
, and for another
n
+
d
n
{displaystyle n+dn}
, and the powers, or reciprocals of the focal lengths, be
f
{displaystyle f}
and
f
+
d
f
{displaystyle f+df}
, then d n {displaystyle dn} is called the dispersion, and n {displaystyle n} the dispersive power of the glass.d f f = d n ( n − 1 ) = 1 n , {displaystyle {dfrac {df}{f}}={dfrac {dn}{(n-1)}}={dfrac {1}{n}},}
- Two thin lenses in contact: let
f
1
{displaystyle f_{1}}
and
f
2
{displaystyle f_{2}}
be the powers corresponding to the lenses of refractive indices
n
1
{displaystyle n_{1}}
and
n
2
{displaystyle n_{2}}
and radii
r
1
′
{displaystyle r'_{1}}
,
r
1
″
{displaystyle r''_{1}}
, and
r
2
′
{displaystyle r'_{2}}
,
r
2
″
{displaystyle r''_{2}}
respectively; let
f
{displaystyle f}
denote the total power, and
d
f
{displaystyle df}
,
d
n
1
{displaystyle dn_{1}}
,
d
n
2
{displaystyle dn_{2}}
the changes of
f
{displaystyle f}
,
n
1
{displaystyle n_{1}}
, and
n
2
{displaystyle n_{2}}
with the color. Then the following relations hold:
- f = f 1 − f 2 = ( n 1 − 1 ) ( 1 / r 1 ′ − 1 / r 1 ″ ) + ( n 2 − 1 ) ( 1 / r 2 ′ − 1 / r 2 ″ ) = ( n 1 − 1 ) k 1 + ( n 2 − 1 ) k 2 {displaystyle f=f_{1}-f_{2}=(n_{1}-1)(1/r'_{1}-1/r''_{1})+(n2-1)(1/r'_{2}-1/r''_{2})=(n_{1}-1)k_{1}+(n_{2}-1)k_{2}} ; and
- d f = k 1 d n 1 + k 2 d n 2 {displaystyle df=k_{1}dn_{1}+k_{2}dn_{2}} . For achromatism d f = 0 {displaystyle df=0} , hence, from (3),
- k 1 / k 2 = − d n 2 / d n 1 {displaystyle k_{1}/k_{2}=-dn_{2}/dn_{1}} , or f 1 / f 2 = − n 1 / n 2 {displaystyle f_{1}/f_{2}=-n_{1}/n_{2}} . Therefore f 1 {displaystyle f_{1}} and f 2 {displaystyle f_{2}} must have different algebraic signs, or the system must be composed of a collective and a dispersive lens. Consequently the powers of the two must be different (in order that f {displaystyle f} be not zero (equation 2)), and the dispersive powers must also be different (according to 4).
Newton falhou em perceber a existência de meios de diferentes poderes dispersivos exigidos pelo acromatismo; consequentemente, ele construiu grandes refletores em vez de refratores. James Gregory e Leonhard Euler chegaram à visão correta de uma falsa concepção do acromatismo do olho; isso foi determinado por Chester More Hall em 1728, Klingenstierna em 1754 e por Dollond em 1757, que construiu os célebres telescópios acromáticos. (Ver telescópio.)
Vidro com poder dispersivo mais fraco (maior vNão.) é nomeado vidro de coroa; que com maior poder dispersivo, vidro de flint. Para a construção de uma lente coletiva acromática (fNão. positivo) segue, por meio da equação (4), que uma lente coletiva I. de vidro de coroa e uma lente dispersiva II. de vidro de flint deve ser escolhido; o último, embora o mais fraco, corrige o outro cromaticamente por seu maior poder dispersivo. Para uma lente dispersiva acromática o converso deve ser adotado. Este é, no presente, o tipo ordinário, por exemplo, do objetivo do telescópio; os valores dos quatro raios devem satisfazer as equações (2) e (4). Duas outras condições também podem ser postuladas: uma é sempre a eliminação da aberração no eixo; a segunda ou a segunda Herschel ou Fraunhofer Condição, o último sendo o melhor vide supra, Monocromático Abertura). Na prática, no entanto, é muitas vezes mais útil evitar a segunda condição, fazendo com que as lentes tenham contato, ou seja, radii igual. De acordo com P. Rudolph (Eder's Jahrb. f. Photog., 1891, 5, p. 225; 1893, 7, p. 221), os objetivos cimentados de lentes finas permitem a eliminação da aberração esférica no eixo, se, como acima, a lente coletiva tem um menor índice de refração; por outro lado, permitem a eliminação do astigmatismo e curvatura do campo de Petdel56. Se o sistema cimentado for positivo, então a lente mais poderosa deve ser positiva; e, de acordo com (4), a maior potência pertence ao poder dispersivo mais fraco (maior vNão.), isto é, vidro de coroa; consequentemente o vidro da coroa deve ter o índice de refração maior para imagens astigmáticas e planas. Em todos os tipos anteriores de vidro, no entanto, a potência dispersiva aumentou com o índice de refração; isto é, vNão. diminuição como nNão. aumentou; mas alguns dos óculos de Jena de E. Abbe e O. Schott eram óculos de coroa de alto índice de refração, e sistemas acromáticos de tais óculos de coroa, com óculos de flint de menor índice de refração, são chamados de novos acromats, e foram empregados por P. Rudolph no primeiro anastigmats (objectivos fotográficos).
Em vez de fazer DfNão. desaparecer, um certo valor pode ser atribuído a ele que produzirá, pela adição das duas lentes, qualquer desvio cromático desejado, por exemplo, suficiente para eliminar um presente em outras partes do sistema. Se as lentes I. e II. ser cimentado e ter o mesmo índice de refração para uma cor, então seu efeito para que uma cor é a de uma lente de uma peça; por tal decomposição de uma lente pode ser feito cromático ou acromático à vontade, sem alterar seu efeito esférico. Se o seu efeito cromático (Df/fNão.) ser maior do que a da mesma lente, isto sendo feito do mais dispersivo dos dois óculos empregados, é denominado hipercromática.
Para duas lentes finas separadas por uma distância DNão. a condição para o achromatism é D= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =v1f1+v2f2Não. D=v_{1}f_{1}+v_{2}f_{2}}; se v1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =v2Não. v_{1}=v_{2}} (por exemplo, se as lentes forem feitas do mesmo vidro), isso reduz a D= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(f1+f2)/2(f_{1}+f_{2})/2}, conhecido como o condição para oculares.
Se uma constante de reprodução, por exemplo, o comprimento focal, ser feito igual para duas cores, então não é o mesmo para outras cores, se dois óculos diferentes são empregados. Por exemplo, a condição para o achromatism (4) para duas lentes finas em contato é cumprida em apenas uma parte do espectro, uma vez que Dn2/Dn1Não. dn_{2}/dn_{1}} varia dentro do espectro. Este fato foi verificado pela primeira vez por J. Fraunhofer, que definiu as cores por meio das linhas escuras no espectro solar; e mostrou que a proporção da dispersão de dois copos variou cerca de 20% do vermelho para o violeta (a variação de vidro e água é de cerca de 50%). Se, portanto, para duas cores, a e b, fum= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =fb)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =fNão. f_{a}=f_{b}=f}, então para uma terceira cor, c, a distância focal é diferente; isto é, se c está entre a e b, então <math alttext="{displaystyle f_{c}fc<fNão. f_{c}<f}<img alt="f_{c}, e vice-versa; estes resultados algébricas seguem do fato de que para o vermelho a dispersão do vidro coroa positiva preponderia, em direção ao violeta que do flint negativo. Estes erros cromáticos de sistemas, que são acromáticos para duas cores, são chamados de espectro secundário, e dependem da abertura e da distância focal da mesma maneira que os erros cromáticos primários.
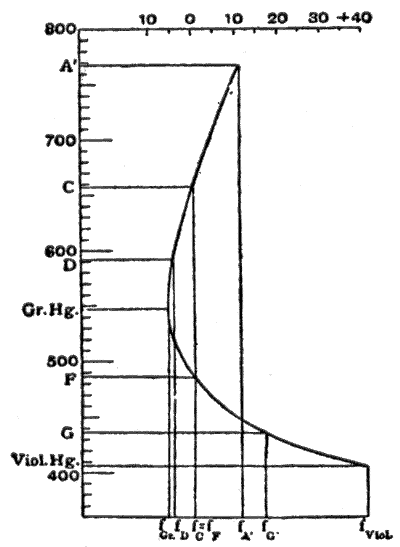
Na fig. 6, tirado de Theorie und Geschichte des photography Objectivs de M. von Rohr, as abcissas são distâncias focais e as ordenadas comprimentos de onda. As linhas de Fraunhofer utilizadas são mostradas na tabela ao lado.
| A ' | C | D | Green Hg. | F | G ' | Violet Hg. |
| 76,7 | 656.3 | 589.3 | 54. | 486.2 | 454.1 | 405.1 nm |
As distâncias focais são feitas iguais para as linhas C e F. No bairro de 550 nm o tangente à curva é paralelo ao eixo de comprimentos de onda; e o comprimento focal varia menos sobre uma gama razoavelmente grande de cor, portanto neste bairro a união de cor é no seu melhor. Além disso, esta região do espectro é a que parece mais brilhante para o olho humano, e consequentemente esta curva do secundário no espectro, obtida por fazer fC= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =fFNão. f_{C}=f_{F}}, é, de acordo com as experiências de Sir G. G. Stokes (Proc. Roy. Soc., 1878), o mais adequado para instrumentos visuais (acromatismo óptico,). De forma semelhante, para sistemas utilizados na fotografia, o vértice da curva de cor deve ser colocado na posição da máxima sensibilidade das placas; isto é geralmente suposto estar em G'; e para realizar isso as linhas de mercúrio F e violeta estão unidos. Este artifício é especialmente adotado em objetivos para fotografia astronômica (acromatismo ativo puro). Para a fotografia comum, no entanto, há esta desvantagem: a imagem na tela de focagem e o ajuste correto da placa sensível fotográfica não estão no registro; na fotografia astronômica esta diferença é constante, mas em outros tipos depende da distância dos objetos. Nesta conta, as linhas D e G' estão unidas para objetivos fotográficos comuns; a imagem óptica, bem como a imagem actínica é cromaticamente inferior, mas ambas estão no mesmo lugar; e, consequentemente, a melhor correção encontra-se em F (isso é conhecido como o correção actínica ou liberdade de foco químico).
Deve haver em duas lentes em contato com as mesmas distâncias focais para três cores a, b e c, i.e. fum= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =fb)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =fc= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =fNão. f_{a}=f_{b}=f_{c}=f}, então a dispersão parcial relativa (nc- Sim. - Sim. nb))(num- Sim. - Sim. nb))(n_{c}-n_{b})(n_{a}-n_{b})} deve ser igual para os dois tipos de vidro empregado. Isto segue considerando a equação (4) para os dois pares de cores ac e bc. Até recentemente nenhum copo era conhecido com um grau de absorção proporcional; mas R. Blair (Trans. Edin. Soc., 1791, 3, p. 3), P. Barlow e F. S. Archer superaram a dificuldade através da construção de lentes fluidas entre paredes de vidro. Fraunhofer preparou óculos que reduziram o espectro secundário; mas o sucesso permanente só foi garantido na introdução dos óculos Jena por E. Abbe e O. Schott. Ao usar óculos que não têm dispersão proporcional, o desvio de uma terceira cor pode ser eliminado por duas lentes, se um intervalo for permitido entre eles; ou por três lentes em contato, que podem nem todos consistir dos óculos antigos. Em unir três cores um acromatismo de uma ordem mais elevada é derivado; há ainda um residual espectro terciário, mas sempre pode ser negligenciado.
A teoria gaussiana é apenas uma aproximação; ainda ocorrem aberrações monocromáticas ou esféricas, que serão diferentes para cores diferentes; e se fossem compensados por uma cor, a imagem de outra cor se mostraria perturbadora. O mais importante é a diferença cromática de aberração do ponto do eixo, que ainda está presente para atrapalhar a imagem, depois que raios para-axiais de cores diferentes são unidos por uma combinação apropriada de vidros. Se um sistema coletivo for corrigido para o ponto do eixo para um comprimento de onda definido, então, devido à maior dispersão nos componentes negativos - os vidros de sílex - a sobrecorreção surgirá para os comprimentos de onda mais curtos (sendo este o erro dos componentes negativos)., e subcorreção para os comprimentos de onda mais longos (o erro das lentes de vidro da coroa preponderando no vermelho). Este erro foi tratado por Jean le Rond d'Alembert e, em especial detalhe, por C. F. Gauss. Aumenta rapidamente com a abertura e é mais importante com aberturas médias do que com o espectro secundário de raios para-axiais; consequentemente, a aberração esférica deve ser eliminada para duas cores e, se isso for impossível, deve ser eliminada para os comprimentos de onda específicos que são mais eficazes para o instrumento em questão (uma representação gráfica desse erro é fornecida em M. von Rohr, Theorie und Geschichte des Photographerischen Objectivs).
A condição para a reprodução de um elemento de superfície no lugar de um ponto nitidamente reproduzido - a constante da relação senoidal também deve ser cumprida com grandes aberturas para várias cores. E. Abbe conseguiu computar objetivas de microscópio livres de erro do ponto do eixo e satisfazendo a condição senoidal para várias cores, que, portanto, de acordo com sua definição, eram aplanáticas para várias cores; tais sistemas ele chamou de apocromáticos. Embora, no entanto, a ampliação das zonas individuais seja a mesma, não é a mesma para o vermelho e para o azul; e há uma diferença cromática de ampliação. Isso é produzido na mesma quantidade, mas em sentido oposto, pelas oculares, que Abbe usou com essas objetivas (oculares compensadoras), de modo que é eliminado na imagem de todo o microscópio. As melhores objetivas de telescópio e objetivas fotográficas destinadas ao trabalho em três cores também são apocromáticas, mesmo que não possuam exatamente a mesma qualidade de correção que as objetivas de microscópio. As diferenças cromáticas de outros erros de reprodução raramente têm importância prática.
Contenido relacionado
Zero absoluto
Carga elétrica
Choque hidrostático