概率模型

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

概率模型还是统计或概率模型是一种数学模型，它包含一组与样本数据（以及来自更大群体的类似数据）的生成相关的统计假设。统计模型通常以高度理想化的形式表示生成数据的过程。

统计模型通常被指定为一个或多个随机变量与其他非随机变量之间的数学关系。因此，统计模型是“理论的正式表示”（Herman Adèr 引用 Kenneth Bollen）。

所有统计假设检验和所有统计估计量都是通过统计模型得出的。更一般地说，统计模型是统计推断基础的一部分。

介绍

非正式地，统计模型可以被认为是具有特定属性的统计假设（或一组统计假设）：该假设允许我们计算任何事件的概率。例如，考虑一对普通的六面骰子。我们将研究关于骰子的两种不同的统计假设。

第一个统计假设如下：对于每个骰子，每个正面（1、2、3、4、5 和 6）出现的概率是 1/6。根据这个假设，我们可以计算出两个骰子出现的概率为 5：1/6×1/6 = 1/36。更一般地，我们可以计算任何事件的概率：例如（1 和 2）或（3 和 3）或（5 和 6）。

另一种统计假设如下：对于每个骰子，正面 5 出现的概率是 1/8（因为骰子是加权的）。根据这个假设，我们可以计算出两个骰子出现的概率为 5：1/8×1/8 = 1/64。但是，我们无法计算任何其他重要事件的概率，因为其他正面的概率是未知的。

第一个统计假设构成了一个统计模型：因为仅凭假设，我们就可以计算出任何事件的概率。替代的统计假设不构成统计模型：因为仅凭假设，我们无法计算每个事件的概率。

在上面的示例中，使用第一个假设，计算事件的概率很容易。但是，对于其他一些示例，计算可能很困难甚至不切实际（例如，它可能需要数百万年的计算）。对于构成统计模型的假设，这样的困难是可以接受的：进行计算不必是切实可行的，只在理论上是可行的。

正式定义

用数学术语来说，一个统计模型一般被认为是一对 ( $S,{\数学{P}}$ )，其中 $是的$ 是可能的观测值的集合，即样本空间， ${\数学{P}}$ 是中的一组概率分布 $是的$ 。

这个定义背后的直觉如下。假设存在由生成观察数据的过程引起的“真实”概率分布。我们选择 ${\数学{P}}$ 表示一组（分布），其中包含充分近似真实分布的分布。

请注意，我们并不要求它 ${\数学{P}}$ 包含真实分布，实际上这种情况很少见。事实上，正如伯纳姆和安德森所说，“模型是对现实的简化或近似，因此不会反映所有的现实”，因此有“所有模型都是错误的”的说法。

该集合 ${\数学{P}}$ 几乎总是参数化： ${\mathcal {P}}=\{P_{{\theta }}:\theta \in \Theta \}$ . 该集合 $\θ$ 定义了模型的参数。一般来说，需要进行参数化，使不同的参数值产生不同的分布，即 $P_{{\theta 1}}}=P_{{\theta 2}}}\右箭头θ1}=\theta 2$ 必须包含（换句话说，必须是单射的）。满足要求的参数化称为可识别的。

一个例子

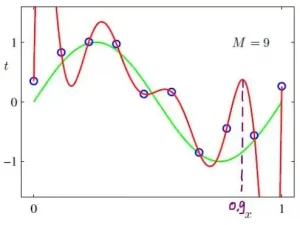
假设我们有一个儿童人口，儿童的年龄在人口中是均匀分布的。孩子的身高会与年龄随机相关：例如，当我们知道孩子 7 岁时，这会影响他身高 1.5 米的概率。我们可以在线性回归模型中形式化这种关系，如下所示：身高 _i = b ₀ + b ₁ 年龄 _i + ε _i ，其中 b ₀ 是截距， b ₁ 是乘以年龄以获得预测的参数高度，ε _i 是误差项， i识别孩子。这意味着身高是按年龄预测的，但有一些误差。

一个合理的模型必须在所有数据点上保持一致。因此，一条直线（身高 _i = b ₀ + b ₁ 年龄 _i ）不能成为数据模型的方程，除非它完全适合所有数据点，即所有点数据都完美地在线上。误差项 ε _i 必须包含在方程中，以使模型在所有数据点上保持一致。

为了进行统计推断，我们首先需要假设 ε _i的一些概率分布。例如，我们可以假设 εi 分布 _是 iid 高斯分布，均值为零。在这种情况下，模型将有 3 个参数： b ₀ 、 b ₁ 和高斯分布的方差。

我们可以用 ( ) 的形式正式指定模型， $S,{\数学{P}}$ 如下所示。我们模型的样本空间 $是的$ 包含所有可能对（年龄、身高）的集合。 $\θ$ = ( b ₀ , b ₁ , σ ) 的每个可能值决定了上的分布 $是的$ ；表示分布由 $P_{{\theta}}$ . 如果 $\θ$ 是的所有可能值的集合 $\θ$ ，则 ${\mathcal {P}}=\{P_{{\theta }}:\theta \in \Theta \}$ 。（参数化是可识别的，这很容易验证。）

在此示例中，模型由 (1) 指定 $是的$ 和 (2) 对做出一些相关假设来确定 ${\数学{P}}$ 。有两个假设：身高可以用年龄的线性函数来近似；近似中的误差分布为 iid Gaussian。这些假设足以说明 ${\数学{P}}$ ——正如它们必然会做的那样。

一般说明

统计模型是一种特殊的数学模型。统计模型与其他数学模型的区别在于统计模型不是确定性的。因此，在数学方程指定的统计模型中，一些变量没有特定的值，而是具有概率分布；也就是说，一些变量是随机的。在上面关于孩子身高的例子中，ε 是一个随机变量；如果没有该随机变量，该模型将是确定性的。

即使被建模的数据生成过程是确定性的，也经常使用统计模型。例如，抛硬币原则上是一个确定的过程。然而，它通常被建模为随机的（通过伯努利过程）。

选择合适的统计模型来表示给定的数据生成过程有时非常困难，并且可能需要了解该过程和相关的统计分析。相关地，统计学家大卫考克斯爵士曾说过：“将主题问题转化为统计模型的方式通常是分析中最关键的部分。”

根据 Konishi & Kitagawa 的说法，统计模型有三个目的。

预测
信息提取
随机结构的描述

这三个目的与 Friendly & Meyer 概述的三个目的基本相同：预测、估计、描述。这三个目的对应于逻辑推理的三种类型：演绎推理、归纳推理、溯因推理。

模型尺寸

假设我们有一个统计模型 ( $S,{\数学{P}}$ ) ${\mathcal {P}}=\{P_{{\theta }}:\theta \in \Theta \}$ 。如果模型具有有限维度，则称该模型是 参数化的。 $\θ$ 在符号中，我们写<img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f309b19bf10f097c61b8cdb76eac39dcb42f122e" alt="{\displaystyle \Theta \subseteq \mathbb {R}其中 k 是一个正整数（ $\数学{R}$ 表示实数；原则上可以使用其他集合）。这里， k 称为模型的维度。

例如，如果我们假设数据来自单变量高斯分布，那么我们假设<img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/3379eb4fa5de81ad44947719a0f7416e0781ff09" alt="{\displaystyle {\mathcal {P}}=\left\{P_{\mu ,\sigma }(x)\equiv {\frac {1}{{\sqrt {2\pi }}\sigma }}\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma0\right\ } }">.

在此示例中，维度 k 等于 2。

再举一个例子，假设数据由我们假设按照具有独立同分布高斯残差（均值为零）的直线分布的点 ( x , y ) 组成：这导致与示例中使用的儿童身高相同的统计模型. 统计模型的维数为3：直线的截距、直线的斜率、残差分布的方差。（请注意，在几何中，直线的维度为 1。）

虽然形式上 {\display style \theta \in \Theta} $\theta \at \theta$ 是具有维度 k的单个参数，但有时它被认为包含 k个单独的参数。例如，对于单变量高斯分布，{\display style \theta} $\θ$ 形式上是维度为 2 的单个参数，但有时被认为包含 2 个单独的参数：均值和标准差。

如果参数集 {\display style \theta}是无限维的，则统计模型是非 参数的。 $\θ$ 如果统计模型具有有限和无限维参数，则它是半参数的。形式上，如果 k 是 {\display style \theta} 的维数 $\θ$ ， n 是样本数，那么半参数和非参数模型都有 {\displaystyle k\rightarrow\infty} $k \rightarrow \infty$ 为 {\display style n \ right arrow \infinity } $n\rightarrow\infty$ 。如果 {\display style k/n \right arrow 0} ${\显示样式 k/n\右箭头 0}$ 像 {\display style n \right arrow \infinity} $n\rightarrow\infty$ ，则模型是半参数的；否则，模型是非参数的。

参数模型是迄今为止使用最广泛的统计模型。关于半参数和非参数模型，大卫考克斯爵士说：“它们通常涉及较少的分布结构和形状假设，但通常包含关于独立性的强假设。”

嵌套模型

不要与多级模型混淆。

如果第一个模型可以通过对第一个模型的参数施加约束来转换为第二个模型，则两个统计模型是 嵌套的。例如，所有高斯分布的集合中嵌套了零均值高斯分布的集合：我们将均值约束在所有高斯分布的集合上以获得零均值分布。_作为第二个 例子，二次模型y = b0 + b1 x + b2 x + ε , _ε ~ ? ( 0 _,σ )

具有嵌套在其中的线性模型y = b0 + b1 x + ε, ε ~ ?( ₀_,σ )

— 我们将参数 b ₂限制为等于 0。

在这两个示例中，第一个模型的维度都高于第二个模型（对于第一个示例，零均值模型的维度为 1）。这种情况经常发生，但并非总是如此。作为不同的示例，具有维度 2 的正均值高斯分布集嵌套在所有高斯分布集内。

比较模型

统计模型的比较是许多统计推断的基础。事实上，Konishi & Kitagawa (2008, p. 75) 指出：“统计推断中的大多数问题都可以被视为与统计建模相关的问题。它们通常被表述为各种统计模型的比较。”

比较模型的常用标准包括： R 、贝叶斯因子、Akaike 信息标准、似然比检验及其泛化、相对似然。

Contenido relacionado

Más resultados...